احتمال المُتغيِّر العشوائي الطبيعي باستعمال الجدول

Probability of Normal Random Variable Using the Table

سنتعرف في درس احتمال المُتغيِّر العشوائي الطبيعي باستعمال الجدول إلى:

إيجاد احتمالات المُتغيِّر العشوائي الطبيعي باستعمال جدول التوزيع الطبيعي المعياري.

 

أولًا: تحويل قيم التوزيع الطبيعي إلى قيم معيارية

يتم تحويل قيم التوزيع الطبيعي إلى قيم معيارية من خلال العلاقة: 

$z=\frac{x-\mu }{\sigma }$

حيث 

$z$:القيمة المعيارية

$x$:القيمة الحقيقية(القيمة الطبيعية)

$\mu$:الوسط الحسابي للتوزيع الطبيعي

$\sigma$:الانحراف المعياري للتوزيع الطبيعي

 

مثال 1:

إذا كان $X$ متُغيِّرًا عشوائيًاطبيعيًا، وسطه الحسابي $60$، وانحرافه المعياري $5$، فأجد القيمة المعيارية $z$ التي تقابل القيمة $x=75$.

الحل:

صيغة  قيم $z$	$z=\frac{x-\mu }{\sigma }$
بتعويض $x=75 , \mu =60 , \sigma =5$	$z=\frac{75-60}{5}$
بالتبسيط	$$\begin{gathered} z=\frac{15}{5} \\ =3 \end{gathered}$$

مثال 2:

إذا كان $X$ متُغيِّرًا عشوائيًاطبيعيًا، وسطه الحسابي $82$ ، وانحرافه المعياري $10$،فأجد القيمة المعيارية $z$ التي تقابل القيمة $x=76$.

الحل:

صيغة  قيم $z$	$z=\frac{x-\mu }{\sigma }$
بتعويض $x=76 , \mu =82 , \sigma =10$	$z=\frac{76-82}{10}$
بالتبسيط	$$\begin{gathered} z=\frac{-6}{10} \\ =-0.6 \end{gathered}$$

مثال 3:

إذا كان $X$ متُغيِّرًا عشوائيًاطبيعيًا، وسطه الحسابي $58$، وانحرافه المعياري $6$، فأجد القيمة المعيارية $z$ التي تقابل القيمة $x=67$.

الحل:

صيغة  قيم $z$	$z=\frac{x-\mu }{\sigma }$
بتعويض $x=67 , \mu =58 , \sigma =9$	$z=\frac{67-58}{9}$
بالتبسيط	$$\begin{gathered} z=\frac{9}{6} \\ =\frac{3}{2}=1.5 \end{gathered}$$

أتحقق من فهمي

إذا كان$X$ متُغيِّرًا عشوائيًاطبيعيًا، وسطه الحسابي$24$، وانحرافه المعياري $5$، فأجد القيمة المعيارية $z$ التي تقابل قيمة $x$ في كلٍّ ممّا يأتي:

             $a) x=29 b) x=18$

الإجابة:

  $$\begin{gathered} a) x=29 \Rightarrow z=1 \\ b) x=18 \Rightarrow z=-1.2 \end{gathered}$$

 

ثانيًا: إيجاد احتمال المُتغيِّر العشوائي الطبيعي(غير المعياري)

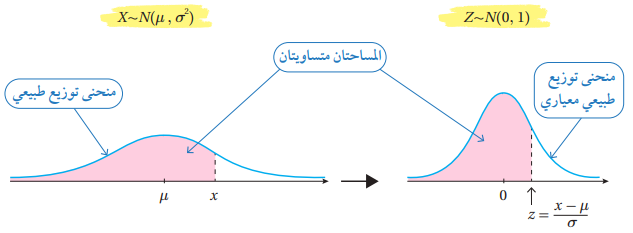
لإيجاد احتمال المُتغيِّر العشوائي الطبيعي نحول قيم المُتغيِّر العشوائي الطبيعي إلى قيم معيارية من خلال الصيغة $z=\frac{x-\mu }{\sigma }$ وعند تحويل القيم الطبيعية إلى قيم معيارية يتحول التوزيع الطبيعي إلى توزيع طبيعي معياري؛ أي إن:

             $Z~N\left(\mu , {\sigma }^2\right) \Rightarrow Z~N\left(0, 1\right)$

وعندها نستطيع استخدام جدول التوزيع الطبيعي المعياري في إيجاد احتمالات المُتغيِّر العشوائي الطبيعي.

ويُمكن ملاحظة ذلك من خلال الشكل الآتي:

      

مثال 4:

إذا كان: $Z~N(70,25)$، فأجد $P\left(X<80\right)$، مُستعمِلاً جدول التوزيع الطبيعي المعياري.

الحل:

صيغة  قيم $Z$	$P\left(X<80\right)=P\left(Z<\frac{80-\mu }{\sigma }\right)$
بتعويض $\mu =70 ,\sigma =5$	$=P(Z<\frac{80-70}{5})$
بالتبسيط	$=P(Z<2)$
باستعمال الجدول	$=0.9772$

مثال 5:

إذا كان: $Z~N(15,3^2)$، فأجد $P(X>12)$، مُستعمِلاً جدول التوزيع الطبيعي المعياري.

الحل:

صيغة  قيم $Z$	$P(X>12)=P(Z>\frac{12-\mu }{\sigma })$
بتعويض$\mu =15 ,\sigma =3$	$=P(Z>\frac{12-15}{3})$
بالتبسيط	$$\begin{gathered} =P(Z>\frac{-3}{3}) \\ =P(Z>-1) \end{gathered}$$
باستعمال خصائص التوزيع الطبيعي المعياري	$=P(z<1)$
باستعمال الجدول	$=0.8413$

مثال 6:

إذا كان: $Z~N(62,{12}^2)$، فأجد $P(X>71)$، مُستعمِلاً جدول التوزيع الطبيعي المعياري.

الحل:

صيغة  قيم $Z$	$P(X>69)=P(Z>\frac{69-\mu }{\sigma })$
بتعويض $\mu =62 , \sigma =12$	$=P(Z>\frac{71-62}{12})$
بالتبسيط	$$\begin{gathered} =P(Z>\frac{9}{12}) \\ =P(Z>0.75) \end{gathered}$$
باستعمال خصائص التوزيع الطبيعي المعياري	$$\begin{gathered} =P(Z>0.75) \\ =1-P(Z<0.75) \end{gathered}$$
باستعمال الجدول$P(Z<0.75)=0.7734$  والتعويض	$=1-0.7734$
بالتبسيط	$=0.2266$

مثال 7:

إذا كان: $Z~N(72,{10}^2)$، فأجد $P(66<X<84)$  مُستعمِلاً جدول التوزيع الطبيعي المعياري.

الحل:

صيغة  قيم $Z$	$P(66<X<84)=P(\frac{66-\mu }{\sigma }<Z<\frac{84-\mu }{\sigma })$
بتعويض$\mu =72 ,\sigma =10$	$=P(\frac{66-72}{10}<Z<\frac{84-72}{10})$
بالتبسيط	$$\begin{gathered} =P(\frac{-6}{10}<Z<\frac{12}{10}) \\ =P(-0.6<Z<1.2) \end{gathered}$$
باستعمال خصائص التوزيع الطبيعي المعياري	$$\begin{gathered} =P(-0.6<z<1.2) \\ =P(z<1.2)-P(z<-0.6) \\ =P(z<1.2)-\left(1-P(z<0.6)\right) \end{gathered}$$
باستعمال الجدول والتعويض$P(Z<1.2)=0.8849$$P(Z<0.6)=0.7257$	$=0.8849-(1-0.7257)$
بالتبسيط	$$\begin{gathered} =0.8849-0.2743 \\ =0.6106 \end{gathered}$$

أتحقق من فهمي

إذا كان:$Z~N(15 , 0.64)$، فأجد مُستعمِلاً جدول التوزيع الطبيعي المعياري كلًّا ممّا يأتي:

$a) P\left(X<15.6\right) b) P\left(X>13.2\right) c) P\left(14.8<X<16\right)$

الإجابة:

                              $$\begin{gathered} a) P(X<15.6)=0.7734 \\ b) P(X>13.2)=0.9878 \\ c) P(14.8<X<16)=0.4931 \end{gathered}$$

مثال 8: من الحياة

تتبع كُتل حبات البرتقال في إحدى مزارع الغور توزيعيًا طبيعيًا، وسطه الحسابي $55 g$، وانحراف معياري $5 g$.

$(a$ ما نسبة عدد حبات البرتقال التي تقل كتلة كُلٍّ منها عن $63 g$؟

$(b$ إذا وضع في شاحنة $4650$ حبة برتقال من إنتاج هذه المزرعة لنقلها إلى السوق المركزي لبيعها، فما عدد حبات البرتقال التي تزيد كتلة كُلٍّ منها عن $70 g$؟

الحل:

$(a$ نسبة عدد حبات البرتقال التي تقل كتلة كُلٍّ منها عن $63 g$ هي:  $P\left(X<63\right)$

صيغة قيم $Z$	$P(X<63)=P\left(Z<\frac{63-\mu }{\sigma }\right)$
بتعويض$\mu =55 , \sigma =5$	$P(X<63)=P(z<\frac{63-55}{5})$
بالتبسيط	$$\begin{gathered} =P(z<\frac{8}{5}) \\ =P(z<1.6) \end{gathered}$$
باستعمال الجدول	$=0.9452$

إذًا، نسبة عدد حبات البرتقال التي تقل كتلة كُلًّ منها عن $63 g$ تساوي: $0.9452$

$(b$ 

الخطوة 1: أجد نسبة عدد حبات البرتقال التي يزيد كتلة كُلًّ منها عن $70 g$

صيغة قيم $Z$	$P(X>70)=P(Z>\frac{70-\mu }{\sigma })$
بتعويض$\mu =55 , \sigma =5$	$=P(Z>\frac{70-55}{5})$
بالتبسيط	$=P(Z>3)$
باستعمال خصائص التوزيع الطبيعي المعياري	ة        $=1-P\left(z<3\right)$
باستعمال الجدول والتعويض$P(Z<3)=0.9987$	$=1-0.9987$
بالتبسيط	$=0.0013$

 إذًا، نسبة عدد حبات البرتقال التي تزيد كتلة كُلٍّ منها عن $70 g$ تساوي: $0.0013$

الخطوة 2: أجد عدد حبات البرتقال التي تزيد كتلة كُلٍّ منها عن $70 g$

حيث أن:

عدد حبات البرتقال التي تزيد  كتلة كُلٍّ منها عن $70 g$  تساوي $\mathrm{النسبة} \times \mathrm{العدد} \mathrm{الكلي}$

         $0013.0 \times 4650=$

        $6\approx$  

عدد حبات البرتقال التي تزيد  كتلة كُلٍّ منها عن $g 70$ تساوي 6 حبات تقريبًا.

أتحقق من فهمي               

إذا كان متوسط أطوال 500 شجرة حرجية في إحدى غابات عجلون هو $8 m$، والانحراف المعياري $2 m$، وكانت الأطوال تتوزع توزيعًا طبيعيًا.

$(a$ اختيرت إحدى الأشجار عشوائيًا ما احتمال أن يزيد طولها على $11 m$؟ 

$(b$ ما عدد الأشجار التي طولها أقل من $7 m$ ؟

الإجابة:

$P\left(X>11\right)=0.0668 (a$

$\mathrm{شجرة} 154 \mathrm{تقريبًا} \mathrm{يساوي} \mathrm{الأشجار} \mathrm{عدد} (b$