رياضيات 9 فصل ثاني

الأجزاءُ المُتناسِبةُ في المُثلَّثاتِ

Proportional Parts in Triangles

فكرةُ الدرسِ : تعرُّفُ الأجزاءِ المُتناسِبةِ في المُثلَّثِ، واستعمالُها لإيجادِ قياساتٍ مجهولةٍ.

أولًا : الأجزاءُ المُتناسِبةُ في المُثلَّث

•• أتذكَّرُ : تعلَّمْتُ سابقًا أنَّهُ يُمكِنُ إثباتُ تشابهِ مُثلَّثينِ باستعمالِ عددٍ منَ المُسلَّماتِ والنظرياتِ مثلِ: التشابهِ بزاويتينِ(AA) ، والتشابهِ بثلاثةِ أضلاعٍ (SSS)، والتشابهِ بضلعينِ وزاويةٍ محصورة (SAS).

 

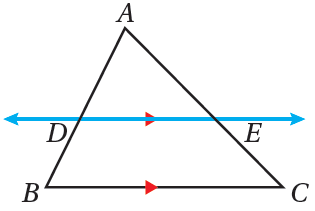
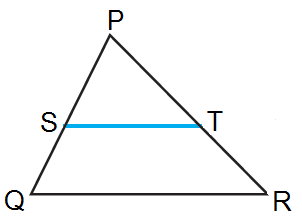
يُبيِّنُ الشكلُ المُجاوِرُ المُثلَّثَ ABC ، حيثُ: ،$\overleftrightarrow{DE}\parallel \stackrel{—}{BC}$  و$\overleftrightarrow{DE}$ يقطعُ $\stackrel{—}{AB}$ في D، ويقطعُ $\stackrel{—}{AC}$ في E. فإنه يُمكن إثبات أنّ المثلثين ΔABC و ΔADE  متشابهان ، وذلكَ باستعمالِ مُسلَّمةِ التشابهِ AA . وبما أنَّ المُثلَّثينِ مُتشابِهانِ، فإنَّ أطوالَ أضلاعِهِما مُتناسِبةٌ، وهذا يقودُنا إلى النظريةِ الآتيةِ.

نظرية ( التناسب في المثلث )

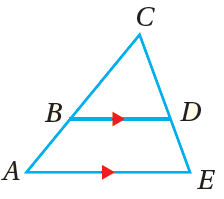
بالكلماتِ : إذا وازى مستقيمٌ ضلعًا منْ أضلاعِ مُثلَّثٍ، وقطعَ ضلعيْهِ الآخرينِ، فإنَّهُ يُقسِّمُهُما إلى قطعٍ مستقيمةٍ مُتناظِرةٍ أطوالُها مُتناسِبةٌ. بالرموزِ : إذا كانَ : $\stackrel{—}{BD}\parallel \stackrel{—}{AE}$ ، فإنّ  $\frac{BA}{CB}=\frac{DE}{CD}$

مثال 1: 

في $△ABC$ إذا كان $\stackrel{—}{DS}\parallel \stackrel{—}{AC}$ و $AD=2cm ,AB=7cm ,CS=2.5cm$ فأجد $SB$

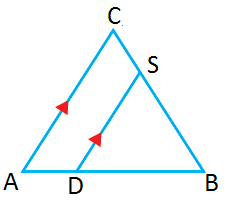
الحل:

نظريةُ الأجزاءِ المُتناسِبةِ: $\frac{AD}{DB}=\frac{CS}{SB}$

بتعويض: $DB=7-2=5$ 

$\frac{2}{5}=\frac{2.5}{SB}\to 2SB=12.5\to SB=6.25cm$

---

ثانيًا : عكسُ نظريةِ التناسبِ في المُثلَّثِ

إنَّ عكسَ نظريةِ التناسبِ في المُثلَّثِ صحيحٌ أيضًا، وهذا ما تنصُّ عليْهِ النظريةُ الآتيةُ.

نظرية (عكسُ نظريةِ التناسبِ في المُثلَّثِ)

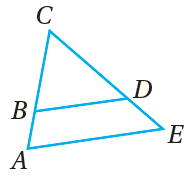
بالكلماتِ : إذا قطعَ مستقيمٌ ضلعينِ في مُثلَّثٍ، وقسَّمَهُما إلى قطعٍ مستقيمةٍ مُتناظِرةٍ أطوالُها مُتناسِبةٌ، فإنَّ المستقيمَ يوازي الضلعَ الثالثَ للمُثلَّثِ. بالرموزِ : إذا كانَ $\frac{AB}{BC}=\frac{ED}{DC}$ ، فإنّ $\stackrel{—}{BD}\parallel \stackrel{—}{AE}$

مثال 2: 

في $△PQR$ إذا كان $PT=12cm, TR=9cm, PS=10cm ,SQ=7.5cm$

بيّن أنّ $\stackrel{—}{ST}\parallel \stackrel{—}{QR}$ مبررًا ذلك.

الحل : 

$\frac{PT}{TR}=\frac{12}{9}=\frac{4}{3}$

$\frac{PS}{SQ}=\frac{10}{7.5}=\frac{4}{3}$

إذن : $\frac{PT}{TR}=\frac{PS}{SQ}=\frac{4}{3}$

وبحسب عكس نظرية التناسب في المثلث ، فإنّ $\stackrel{—}{ST}\parallel \stackrel{—}{QR}$

---

ثالثًا : القطعةُ المُنصِّفةُ في المُثلَّث

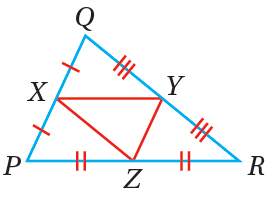
القطعةُ المُنصِّفةُ في المُثلَّثِ  : هيَ قطعةٌ مستقيمةٌ طرفاها نقطتا منتصفِ ضلعين في المُثلَّثِ، وفي كلِّ مُثلَّثٍ ثلاثُ قطعٍ مُنصِّفةٍ. فمثلًا ، القطعُ المُنصِّفةُ في $△PQR$ المُجاور هي : $\overline{XY} , \overline{YZ} , \overline{XZ}$

•• توجدُ علاقتان بينَ القطعةِ المُنصِّفة في المُثلَّث والضلعِ المُقابِل لها، وهما مُوضَّحتان في النظرية الآتية.

نظرية ( القطعة المنصفة في المثلث )

 

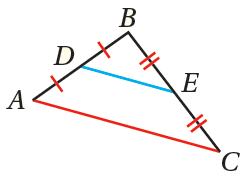
بالكلماتِ: القطعةُ المُنصِّفةُ في المُثلَّثِ توازي الضلعَ المُقابِلَ لها، وطولُها يساوي

نصفَ طولِ ذلكَ الضلعِ.

بالرموزِ : إذا كانَتِ النقطةُ D والنقطةُ E هما نقطتَيْ منتصفِ$\stackrel{—}{BC}و \stackrel{—}{AB}$ على الترتيبِ،فإنَّ:

$\stackrel{—}{DE}\parallel \stackrel{—}{AC} and DE=\frac{1}{2} AC$

بالكلماتِ: القطعةُ المُنصِّفةُ في المُثلَّثِ توازي الضلعَ المُقابِلَ لها، وطولُها يساوي نصفَ طولِ ذلكَ الضلعِ. بالرموزِ : إذا كانَتِ النقطةُ D والنقطةُ E هما نقطتَيْ منتصفِ $\overline{ BC} و \overline{AB}$ على الترتيبِ،فإنَّ:  $\overline{DE} \parallel \overline{AC} and DE = \frac{1}{2} AC$

مثال 3 : 

استخدم المعلومات المُعطاة في الرسم المُجاور لإيجاد كل مما يأتي : 

$1) RN 2) CB 3) m\angle MCN 4) m\angle RMC$

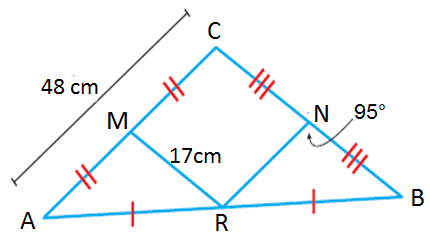
الحل : 

1) طول $\overline{RN}$ 

$RN=\frac{1}{2}AC=\frac{1}{2}\left(48\right)=24cm$

2) طول $\overline{CB}$

$MR=\frac{1}{2}CB$

$17=\frac{1}{2}CB\to CB=34cm$

3) قياس  $\angle MCN$

$\angle MCN\cong \angle RNB$	نظريةُ الزاويتينِ المُتناظرتين
$m\angle MCN=m\angle RNB$	تعريفُ تطابقِ الزوايا
$m\angle MCN=95°$	بالتعويضِ

---

4) قياس $\angle RMC$

$m\angle MCN+m\angle RMC=180°$	نظريةُ الزاويتينِ المُتحالفتين
$95°+ m\angle RMC=180°$	بتعويض $m\angle MCN=95°$
$m\angle RMC=180°-95°$	بحل المعادلة
$m\angle RMC=85°$	بالتبسيط