الرياضيات فصل أول

أستعد لدراسة وحدة التفاضل: كتاب التمارين صفحة (13-14)

 

قبل أن نبدأ بدراسة وحدة التفاضل علينا تذكر مجموعة من المفاهيم التي درسناها في صفوف سابقة، منها:

1. كتابة المقدار الجبري في أبسط صورة.

2. التحويل من الصيغة الجذرية إلى الصيغة الأسية.

3.مشتقة اقتران القوة.

 

أولًا: كتابة المقدار الجبري في أبسط صورة:

* عند ضرب مقدارين جبريين:

1. افصل المقدار الجبري المعطى إلى حدود _إن لزم الأمر-

2. استخدم خاصية التوزيع منتبهًا إلى الإشارات.

3.اجمع الحدود المتشابهة

4. اكتب المقدار بأبسط صورة

 

مثال: جد ناتج ضرب كل مما يأتي في أبسط صورة:

          $a) -6x (x-8) b) \left(3x-7\right)\left(2x-5\right)$

 

الحل:

 

$a) -6x (x-8)$
$-6x (x-8)=-6x( x)-6x (-8)$	الخاصية التوزيعية
$=-6x^2 +48 x$	المقدار في أبسط صورة

$b) (3x-7)(2x-5)$
$(3x-7)(2x-5)=3x(2x-5) + -7(2x-5)$	افصل المقدار $(3x-7)$  إلى حدين ، ثم اضرب كلًا منهما في المقدار $(2x-5)$
$=(6x^2-15x) + (-14x+35)$	الخاصية التوزيعية
$=6x^2-15x-14x+35$	جمع الحدود المتشابهة
$=6x^2-29x+35$	المقدار في أبسط صورة

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

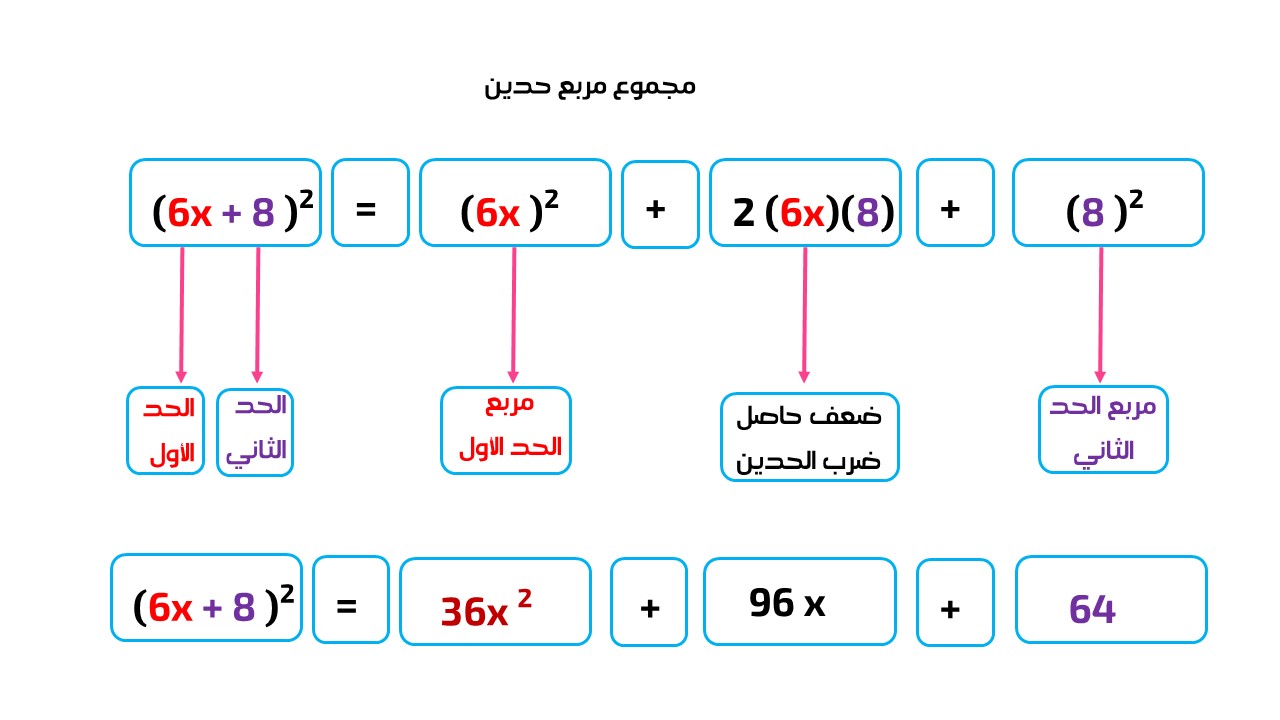
* عند إيجاد مربع مجموع حدين: ${\left(x+y\right)}^2$

مربع مجموع حدين يساوي مربع الحد الأول + 2× الحد الأول × الحد الثاني + مربع الحد الثاني

وبالرموز:

                                   ${\left(x+y\right)}^2 = x^2 + 2x y + y^2$

 

 

 

 

 

مثال: جد ناتج ضرب كل مما يأتي في أبسط صورة:

            $a) {(2x+5)}^2 b) {(3x-7)}^2$

 

الحل:

    $$\begin{gathered} a) {(2x+5)}^2 =4x^2 +20x +25 \\ b) {(3x-7)}^2 =9x^2 -42 x +49 \end{gathered}$$

 

---

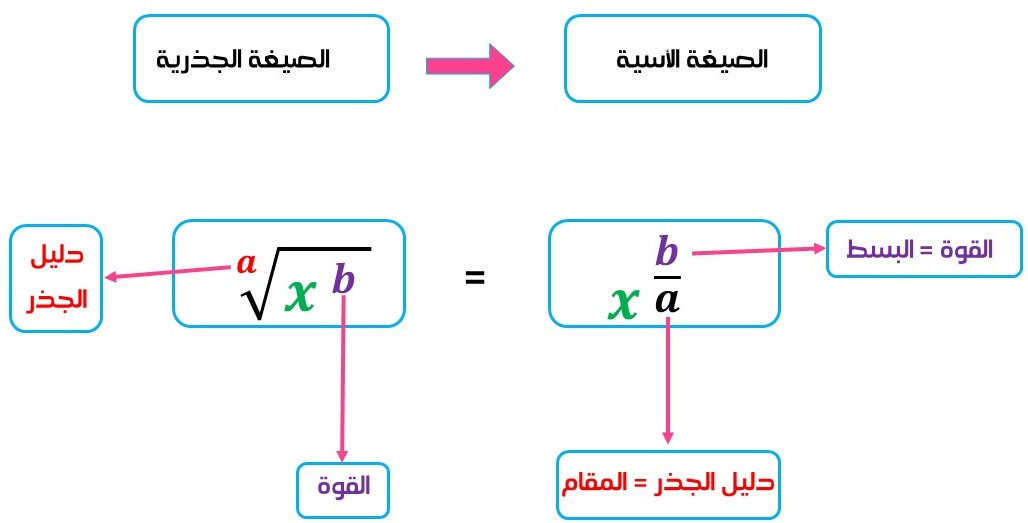
ثانيًا: التحويل من الصيغة الجذرية إلى الصيغة الأسية:

* عند التحويل من الصيغة الجذرية إلى الصيغة الأسية، عليك تذكر مجموعة من قوانين الأسس أهمها:

1. القوة السالبة:  $a^{-1} = \frac{1}{a}$

2.الصورة الجذرية: $a^{\frac{m}{n}}= \sqrt[n]{a^m}$

 

ونلخص طريقة التحويل من الصيغة الجذرية إلى الصيغة الأسية بالمخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: حول كل مما يأتي من الصيغة الجذرية إلى الصيغة الأسية:

                                         $a) \sqrt[15]{x^9} b) \frac{8}{\sqrt[5]{x-6}}$

 

الحل:

                                             $$\begin{gathered} a) \sqrt[15]{x^9} = x^{\frac{9}{15}} = x^{\frac{3}{5}} \\ b) \frac{8}{\sqrt[5]{x-6}}=\frac{8}{{(x-6)}^{{\displaystyle \frac{1}{5}}}}=8 {\left(x-6\right)}^{\frac{-1}{5}} \end{gathered}$$

 

---

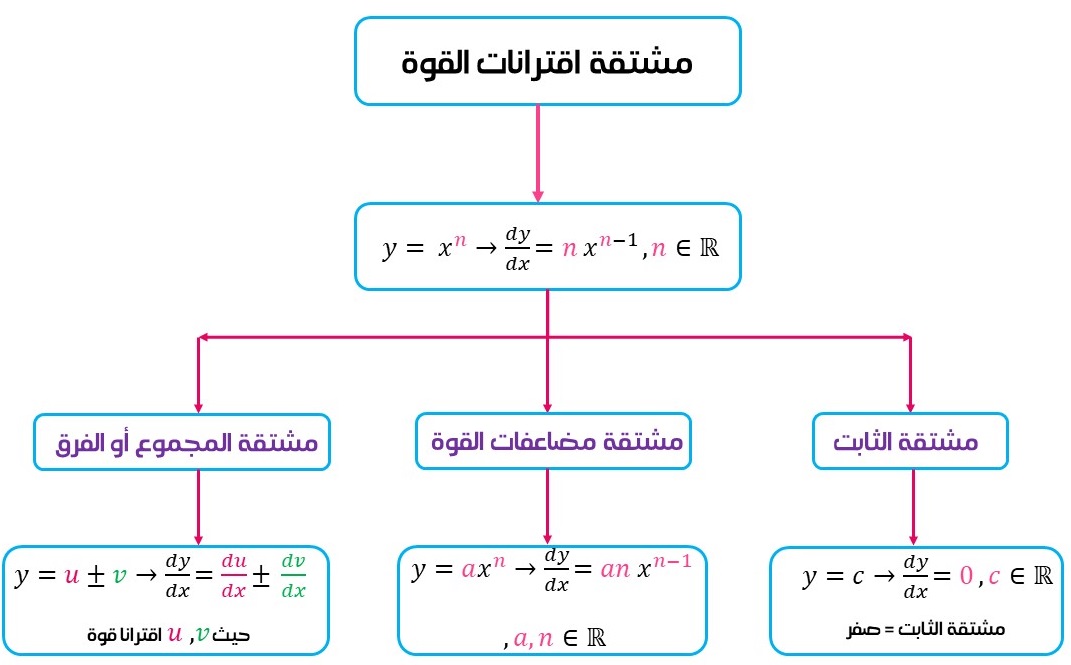
ثالثًا:مشتقة اقتران القوة:

مشتقة اقتران القوة تعني أنه عند اشتقاق الاقتران: $\mathit{y}\mathbf{=}{\mathit{x}}^{\mathbf{n}}$ حيث n عدد حقيقي، فإن أُس $\mathit{x}$ في المشتقة يكون أقل بواحد من أس $\mathit{x}$ في الاقتران الأصلي،

ومعامل $\mathit{x}$ في المشتقة يساوي أُس $\mathit{x}$ في الاقتران الأصلي.

وبالرموز: إذا كان $\mathit{y}\mathbf{=}{\mathit{x}}^{\mathbf{n}}$ ، حيث $\mathit{n}$ عدد حقيقي، فإن $\frac{\mathbf{d}\mathbf{y}}{\mathbf{d}\mathbf{x}}\mathbf{=}\mathit{n}\mathbf{ }{\mathit{x}}^{\mathbf{n}\mathbf{-}\mathbf{1}}$

توجد أيضًا بعض القواعد التي تسهل عملية إيجاد مشتقة الاقترانات التي تتضمن حدودها اقترانات القوة، ونلخصها بالمخطط الآتي:

 

مثال: جد مشتقة كل مما يأتي:

           $a) f(x)=\frac{6x^4 - 2\sqrt{x}}{x^3} b) f\left(x\right)=\frac{1}{\sqrt[3]{x}}+x(5x^3-4) +10$

 

 

الحل:

$a) f(x)=\frac{6x^4 - 2 \sqrt{x}}{x^3}$
$= \frac{6x^4}{x^3}- \frac{2\sqrt{x}}{x^3}$	بقسمة كل حد في البسط على $x^3$
$= 6x -2 x^{-\frac{5}{2}}$	بكتابة الاقتران بالصورة الأسية
$f\text{'}\left(x\right)= 6 + 5 x^{-\frac{7}{2}}$	قاعدتا: مشتقة مضاعفات القوة، ومشتقة الفرق
$= 6 +\frac{5}{\sqrt{x^7}}$	تعريف الأس السالب، الصورة الجذرية

 

 

$b) f(x)=\frac{1}{\sqrt[3]{x}}+x(5x^3-4) +10$
$= x^{-\frac{1}{3}} + 5x^4 -4x +10$	بكتابة الاقتران بالصورة الأسية
$f\text{'}\left(x\right)=-\frac{1}{3} x^{-\frac{4}{3}} + 20 x^3 -4$	قواعد: مشتقة مضاعفات القوة، ومشتقة الفرق، مشتقة المجموع، مشتقة الثابت
$=-\frac{1}{3 \sqrt[3]{x^4}} + 20 x^3 -4$	تعريف الأس السالب، الصورة الجذرية