الرياضيات فصل ثاني

كتاب التمارين صفحة 6:

قبل دراسة وحدة التكامل، على الطالب التأكد من إتقانه لمهارات أساسية قد تعلمها في صفوف سابقة وخلال الفصل الدراسي الأول مثل:

1. التحويل من الصورة الأسية إلى الصورة الجذرية والعكس.

2. إيجاد قيمة اقتران عند نقطة ما.

3. إيجاد مشتقة اقترانات مختلفة.

4. إعادة تعريف اقتران القيمة المطلقة.

 

أولًا: التحويل من الصورة الأسية إلى الصورة الجذرية والعكس:

لقد درست سابقًا أنه يمكن كتابة الأسس النسبية على صورة جذرية وكذلك كتابة الجذور على صورة أسية ، وذلك من خلال:

 

 

 

 

 

 

 

ملاحظة: إذا كان y عددا زوجيا، فيجب أن يكون b عددا حقيقا موجبا ليكون العدد  معرفا على الأعداد الحقيقية وإذا كان y عددا فرديا، فيجب أن يكون b عددا حقيقيا.

إذن عند التحويل من الصورة الأسية $b^{\frac{x}{\mathrm{y}}}$ إلى الصورة الجذرية $\sqrt[\mathrm{y}]{b^x}$ فإنّ:

1) المقام بالأس النسبي يصبح دليل الجذر.

2) البسط بالأس النسبي يصبح القوة للجذر ${\left(\sqrt[\mathrm{y}]{\mathrm{b}}\right)}^{{}^x} = \sqrt[\mathrm{y}]{b^x}$.

مثال: اكتب الصورة الأسية في صورة جذرية، والصورة الجذرية في صورة أسية ، في كل مما يأتي:                                                                                                                     $$\begin{gathered} 1) y^{\frac{1}{9}} \\ 2) x^{\frac{3}{8}} \\ 3) \sqrt[5]{p} \\ 4) \sqrt[7]{u^5} \end{gathered}$$

الحل:

الســـــــــــــــــؤال	الصورة الأسية/ الصورة الجذرية
$1) y^{\frac{1}{9}}$	$\sqrt[9]{y}$      الصورة الجذرية
$2) x^{\frac{3}{8}}$	$\sqrt[8]{x^{\mathbf{3}}}$  الصورة الجذرية
$3) \sqrt[5]{p}$	$p^{\frac{1}{5}}$     الصورة الأسية
$4) \sqrt[7]{u^5}$	$u^{\frac{5}{7}}$   الصورة الأسية

 

 

 

 

 

 

 

 

 

 

 

 

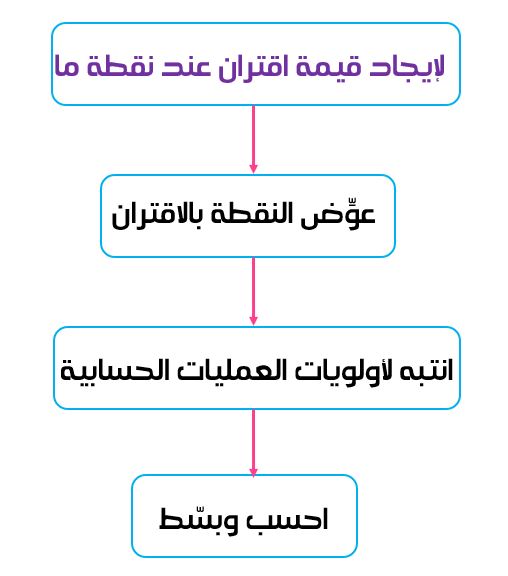
ثانيًا:إيجاد قيمة اقتران عند نقطة ما:

عند إيجاد قيمة اقتران عند نقطة ما فعليك:

1) تعويض النقطة المطلوبة بالاقتران.

2) مراعاة أولويات العمليات الحسابية.

3) تبسيط القيم الناتجة للوصول إلى الإجابة.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: جد قيمة كل من الاقترانات الآتية عند قيمة $x$ المعطاة:

                                                                           $$\begin{gathered} 1) f(x) = x^{4 }- 3x^2 + 2x - 7 , x=2 \\ 2) f(x) = \sqrt[3]{x^{2 }}+ 2x , x=-8 \\ 3) f(x) =e^{x^2-2x} +5x^{2 }+ 5x , x=-1 \end{gathered}$$

الحل:

$1) f(x) = x^{4 }- 3x^2 + 2x - 7 , x=2$
$f\left(2\right) = {\left(2\right)}^{4 }- 3{\left(2\right)}^2 + 2\left(2\right) - 7$	بتعويض قيمة $x$
$= 16- 3\times 4 + 4 - 7$	بإيجاد قيمة الأسس
$$\begin{gathered} = 16- 12 + 4 - 7 \\ =4-3 \\ =1 \end{gathered}$$	بالتبسيط ومراعاة أولويات العمليات الحسابية

 

 

 

 

 

 

 

$2) f(x) = \sqrt[3]{x^{2 }}+ 2x , x=-8$
$f(-8) = \sqrt[3]{{\left(-8\right)}^{2 }}+ 2\left(-8\right)$	بتعويض قيمة $x$
$$\begin{gathered} = \sqrt[3]{64}+ -16 \\ =4-16 \\ =-12 \end{gathered}$$	بالتبسيط ومراعاة أولويات العمليات الحسابية

 

 

 

 

 

 

 

 

$3) f(x) =e^{x^2-2x} +5x^{2 }+ 5x , x=-1$
$f(-1) =e^{{(-1)}^2-2(-1)} +5{(-1)}^{2 }+ 5(-1)$	بتعويض قيمة $x$
$$\begin{gathered} =e^{1+2} +5- 5 \\ =e^3 \end{gathered}$$	بالتبسيط

 

 

 

 

 

 

 

 

 

---

 

ثالثًا:إيجاد مشتقة اقترانات مختلفة:

تعلمنا إيجاد مشتقة اقترانات عدة في وحدة التفاضل بالفصل الدراسي الأول، وأهمها:

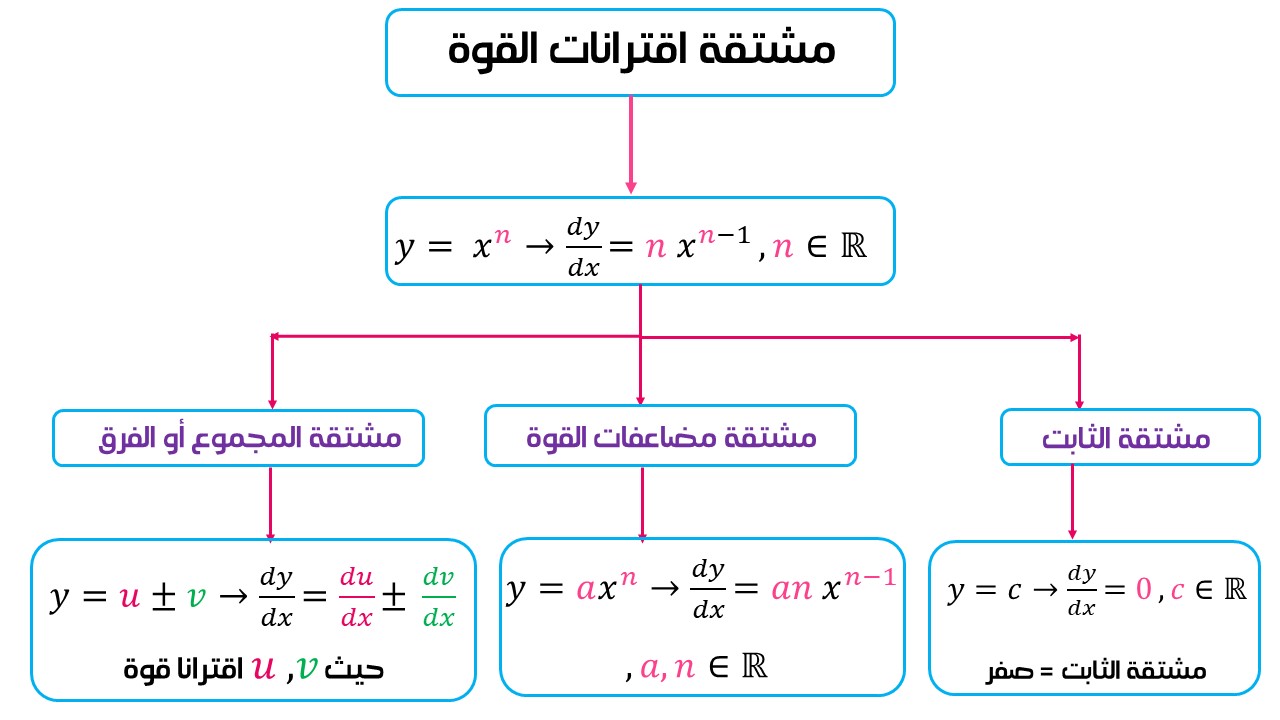
أولًا: مشتقة اقترانات القوة:

يمكن مراجعة المخطط الآتي لتتذكر مشتقة اقترانات القوة:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: جد مشتقة كل من الاقترانات الآتية:

                      $$\begin{gathered} 1) f\left(x\right)= 5 x^7 \\ 2) f\left(x\right) = \sqrt[3]{x} + 2x^3 +7 \end{gathered}$$

الحل:

1) مشتقة الاقتران $f\left(x\right)= 5 x^7$ هي: $f\text{'}\left(x\right)= 35 x^6$

2) مشتقة الاقتران $f\left(x\right) = \sqrt[3]{x} + 2x^3 +7$ هي:

$$\begin{gathered} f\left(x\right) = \sqrt[3]{x} + 2x^3 +7 \\ = x^{\frac{1}{3 }} + 2x^3 +7 \end{gathered}$$	الاقتران
$$\begin{gathered} f\text{'}\left(x\right) =\frac{1}{3} {\left(x\right)}^{-\frac{2}{3}}+ 6x^2 \\ =\frac{1}{3 \sqrt[3]{x^2}}+ 6x^2 \end{gathered}$$	مشتقة الاقتران

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

ثانيًا: قاعدة السلسلة:

يمكن استخدام قاعدة السلسلة لإيجاد مشتقة الاقتران المركب؛ حيث تساوي حاصل ضرب مشتقة الاقتران الداخلي ومشتقة الاقتران الخارجي، ويمكن تلخيصها بالمخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ويمكن الاستفادة من قاعدة السلسلة لإيجاد قاعدة سلسلة القوة، كما في المخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: جد مشتقة كل من الاقترانات الآتية:

                                                      $$\begin{gathered} 1) f\left(x\right)= {(5 x^4 +2x^2)}^3 \\ 2) f\left(x\right) = \sqrt[7]{(4x^3-5x)} \end{gathered}$$

الحل:

1) مشتقة الاقتران $f\left(x\right)= {(5 x^4 +2x^2)}^3$ هي :

              $f\text{'}\left(x\right)=3 {(5 x^4 +2x^2)}^2 \left(20 x^3 +4x\right)$

 

2) مشتقة الاقتران $f\left(x\right) = \sqrt[7]{(4x^3-5x)}$ هي :

          $$\begin{gathered} f\text{'}\left(x\right) = \frac{1}{7} {\left(4x^3-5x\right)}^{-\frac{6}{7}} \left(12x^2 -5\right) \\ = \frac{12x^2 -5}{7 \sqrt[7]{{\left(4x^3-5x\right)}^6}} \end{gathered}$$

---

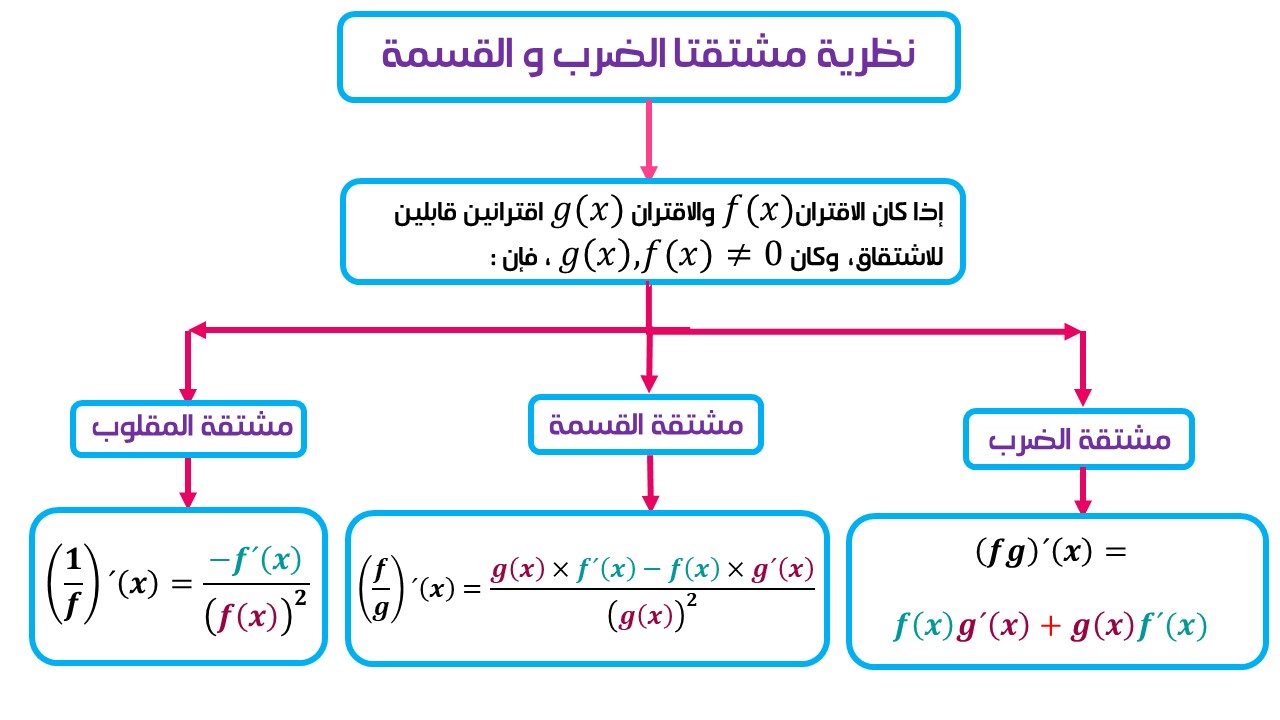
ثالثًا: مشتقتا الضرب والقسمة:

يمكن تلخيص مشتقتا الضرب والقسمة من خلال المخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: جد مشتقة كل من الاقترانات الآتية:

                   $$\begin{gathered} 1) f(x)=(x^4-3x\left)\right(2x^3+4) \\ 2) f\left(x\right)=\frac{x^4}{2x^3+4} \\ 3) f(x)=\frac{1}{5+3x^4} \end{gathered}$$

الحل:

1) لإيجاد مشتقة الاقتران $f\left(x\right)=(x^4-3x)(2x^3+4)$ فإننا نتبع الخطوات الآتية:

$f\text{'}\left(x\right)=\left(x^4-3x\right)\frac{d}{dx}\left(2x^3+4\right)+\left(2x^3+4\right)\frac{d}{dx}(x^4-3x)$	باستخدام قاعدة مشتقة الضرب
$=\left(x^4-3x\right)\left(6x^2\right)+\left(2x^3+4\right)\left(4x^3-3\right)$	قواعد مشتقة كثيرات الحدود، مشتقة الجمع، مشتقة الطرح
$=\left(6x^6-18x^3\right)+\left(8x^6+16x^3-6x^3-12\right)$	خاصية التوزيع
$=14x^6-8x^3-12$	التبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2) لإيجاد مشتقة الاقتران $f\left(x\right)=\frac{x^4}{2x^3+4}$ فإننا نتبع الخطوات الآتية:

$f\text{'}\left(x\right)=\frac{\left(2x^3+4\right){\displaystyle \frac{d}{dx}}\left(x^4\right) - \left(x^4\right)\frac{d}{dx}(2x^3+4)}{{\left(2x^3+4\right)}^2}$	باستخدام قاعدة مشتقة القسمة
$=\frac{\left(2x^3+4\right)\left(4x^3\right) - \left(x^4\right)\left(6x^2\right)}{{\left(2x^3+4\right)}^2}$	قاعدتا مشتقة كثيرات الحدود، مشتقة الجمع.
$=\frac{\left(8x^6+16 x^3\right) - \left(6x^6\right)}{{\left(2x^3+4\right)}^2}$	خاصية التوزيع
$=\frac{2x^6+16 x^3 }{{\left(2x^3+4\right)}^2}$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) لإيجاد مشتقة الاقتران $f\left(x\right)=\frac{1}{5+3x^4}$  فإننا نتبع الخطوات الآتية:

$f\text{'}\left(x\right)=\frac{-{\displaystyle \frac{d}{dx}}(5+3x^4)}{{(5+3x^4)}^2}$	قاعدة مشتقة المقلوب
$=\frac{-12x^3}{{(5+3x^4)}^2}$	قاعدتا مشتقة اقتران القوة، مشتقة الجمع.

 

 

 

 

 

 

 

 

 

---

رابعًا: مشتقتا الاقتران الأسي الطبيعي والاقتران اللوغاريتمي الطبيعي:

يمكن تلخيص مشتقتا الاقتران الأسي الطبيعي والاقتران اللوغاريتمي الطبيعي من خلال المخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: جد مشتقة كل من الاقترانات الآتية:

                         $$\begin{gathered} 1) f(x) = e^{4x-2} -10 x \\ 2) f\left(x\right) = x^7 \ln x \\ 3) f(x) = \frac{\ln x}{x + e^x} \end{gathered}$$

  الحل:

1) مشتقة الاقتران $f\left(x\right) = e^{4x-2} -10 x$ هي: $f\text{'}\left(x\right) = 4 e^{4x-2} -10$

 

 

2) مشتقة الاقتران $f\left(x\right) = x^7 \ln x$ هي: $f\text{'}\left(x\right) = x^7 \left(\frac{1}{x}\right)+\left(7x^6\right)(ln x)$                                        $= x^6 +7x^6 ln x$

3) مشتقة الاقتران $f\left(x\right) = \frac{\ln x}{x + e^x}$ هي:

$f\left(x\right) = \frac{ln x}{x + e^x}$	الاقتران المعطى
$f\text{'}\left(x\right) = \frac{\left(x + e^x\right)\left({\displaystyle \frac{1}{x}}\right) - \left(\ln x\right)\left(1 + e^x\right)}{{\left(x + e^x\right)}^2}$	باستخدام قاعدة مشتقة القسمة

             

 

---

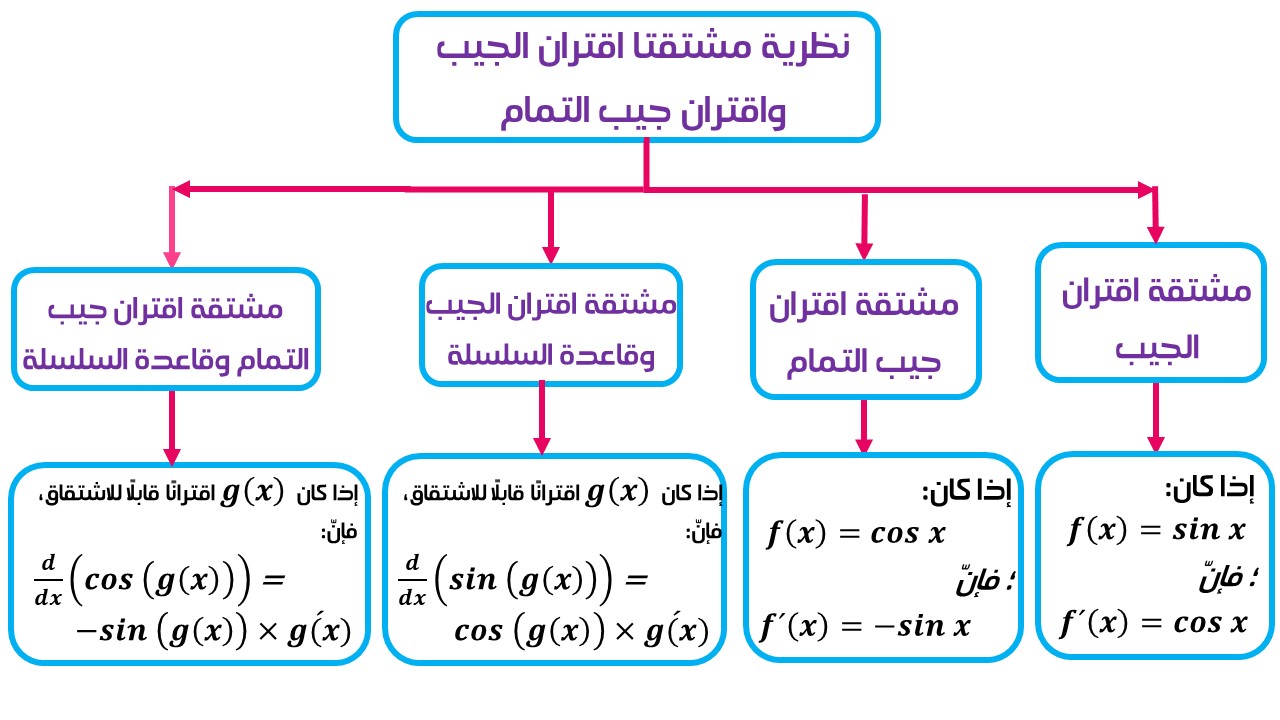
خامسًا: مشتقتا اقتران الجيب واقتران جيب التمام:

تعلمت خلال الفصل الدراسي الأول كيفية إيجاد مشتقة اقترانات الجيب وجيب التمام ، ويمكنك تذكرها من خلال المخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال: جد مشتقة كل من الاقترانات الآتية:

                 $$\begin{gathered} 1) f(x) = \sin 5 x - 2 \cos 7x \\ 2) f\left(x\right)= x^3 \cos x - e^x \sin x \end{gathered}$$

الحل:

1) مشتقة الاقتران $f\left(x\right) = sin 5 x - 2 cos 7x$  هي: $f\text{'}\left(x\right) =5 cos 5 x + 14 sin 7x$

2) مشتقة الاقتران $f\left(x\right)= x^3 \cos x - e^x \sin x$ هي:     

$f\left(x\right)= x^3 cosx - e^x sinx$	الاقتران المعطى
$f^{\text{'}}\left(x\right)= x^3 \frac{d}{dx}\left(\cos x\right)+\cos x \frac{d}{dx} \left(x^3\right) - e^x \frac{d}{dx} \left(sinx\right)-sinx \frac{d}{dx}\left(e^x\right)$	باستخدام قاعدة مشتقة الضرب
$= x^3 (- \sin x)+\cos x (3 x^2) - e^x (\cos x)-sinx \left(e^x\right)$	مشتقة الجيب وجيب التمام والاقتران الأسي
$=- x^3 \sin x+3 x^2 \cos x -e^x \cos x -e^x sinx$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

رابعًا:إعادة تعريف القيمة المطلقة :

يُعتبر اقتران القيمة المطلقة  من أهم الاقترانات  التي يجب تذكرها والتمكن من كيفية إعادة تعريفها، ويمكن تذكر ذلك من خلال الخطوات الآتية:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

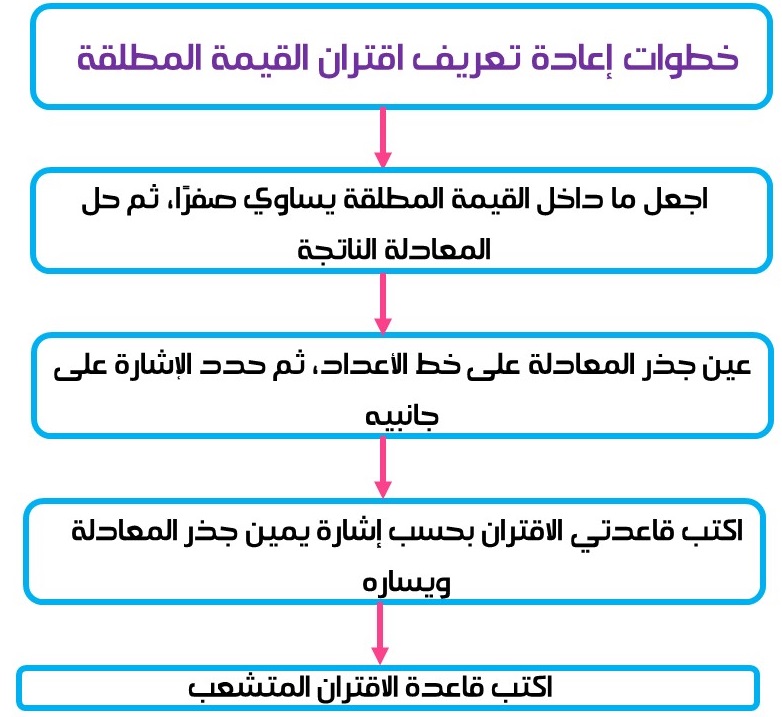
ويمكن تطبيق تلك الخطوات من خلال الأمثلة الآتية:

مثال(1) : أعد تعريف اقتران القيمة المطلقة $f\left(x\right) = \left|x-3\right|$

الحل :

$x - 3 = 0$	بجعل ما داخل القيمة المطلقة يساوي صفرًا
$x = 3$	بحل المعادلة
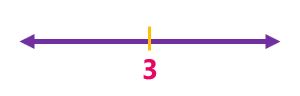	بتعيين الجذر على خط الأعداد
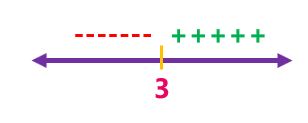	بتحديد الإشارة على جانبيه باستخدام التعويض:   بأخذ عدد أكبر من 3 مثل : 4 وتعويضه بالاقتران x-3  فيكون الناتج 1 ( ولو أخذت أي عدد آخر أكبر من 3 ستكون إشارة الناتج موجبة)   وبأخذ عدد أصغر من 3 مثل 0 وتعويضه بالاقتران x-3  فيكون الناتج 3- ( ولو أحذت أي عدد آخر أصغر من 3 فستكون إشارة الناتج سالبة)
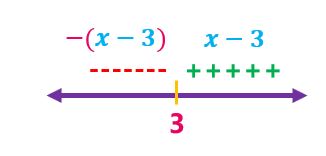	كتابة قاعدتي الاقتران بحسب إشارة يمين جذر المعادلة ويساره: الجزء الموجب: الاقتران كما هو داخل القيمة المطلقة (3-x) الجزء السالب: الاقتران الذي داخل القيمة المطلقة مضروبًا بـ(1-)
$f\left(x\right) = \left\{\begin{array}{l}3-x , x <3\\ x-3 , x \ge 3\end{array}\right.$	كتابة قاعدة الاقتران المتشعب(بالاعتماد على خط الأعداد السابق)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال(2) : أعد تعريف اقتران القيمة المطلقة $f\left(x\right) = |5x+10|$

الحل :

$5x+10 =0$	بجعل ما داخل القيمة المطلقة يساوي صفرًا
$$\begin{gathered} 5x+10 -10=-10 \\ 5x = -10 \\ \frac{5}{5}x = \frac{-10}{5} \\ x = -2 \end{gathered}$$	بحل المعادلة : اطرح 10 من طرفي المعادلة ثم اقسم الطرفين على 5 ثم التبسيط
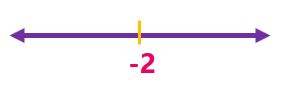	بتعيين الجذر على خط الأعداد
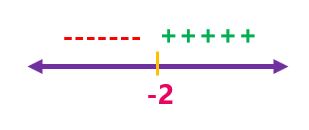	بتحديد الإشارة على جانبيه باستخدام التعويض:   بأخذ عدد أكبر من 2- مثل : 0 وتعويضه بالاقتران 5x+10  فيكون الناتج 10 ( الإشارة موجبة)   وبأخذ عدد أصغر من 2- مثل 3- وتعويضه بالاقتران 5x+10  فيكون الناتج 5- ( الإشارة سالبة)
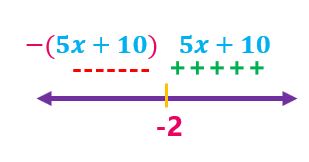	كتابة قاعدتي الاقتران بحسب إشارة يمين جذر المعادلة ويساره: الجزء الموجب: الاقتران كما هو داخل القيمة المطلقة (5x+10) الجزء السالب: الاقتران الذي داخل القيمة المطلقة مضروبًا بـ(1-)
$f\left(x\right) = \{\begin{array}{l}-5x-10 , x <-2\\ 5x+10 , x \ge -2\end{array}$	كتابة قاعدة الاقتران المتشعب(بالاعتماد على خط الأعداد السابق)