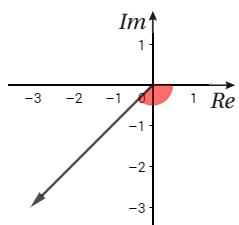رياضيات فصل أول

تواجه علماء الهندسة الكهربائية و الفيزياء معادلات رياضية لا توجد لها حلول حقيقية.

مما جعل علماء الرياضيات يبتكرون توسعة للنظام العددي الحقيقي، مما أدى الى ابتكار (مجموعة الأعداد المركبة (c)).

و من أشهر المعادلات التي لا يوجد لها حلول حقيقية، المعادلة:    $x^2+1=0$ ، حيث أن حلولها هي:   $x = \pm \sqrt{-1}$ .

و لأنه لا يوجد أعداد حقيقية مربعها عدد سالب، ابتكر علماء الرياضيات ( الوحدة التخيلية) و رمزوا لها بالرمز (i) حيث أن $i^2=-1$

و بذلك، فإن i و i- هما الجذران التربيعيان للعدد (1-) لأن:   $i^2 = {(-i)}^2 = -1$ .

و يطلق على الوحدة التخيلية i: الجذر التربيعي الرئيس للعدد 1-

و تم توسعة النظام العددي الحقيقي بإنشاء مجموعة الأعداد المركبة (c)

و التي تتكون من مجموعة جميع الأعداد التي تكتب على صورة  a +ib 

حيث a و b أعداد حقيقية، و يسمى كلا من :

العدد a: الجزء الحقيقي من العدد المركب  a +ib

العدد b: الجزء التخيلي من العدد المركب  a+ib

و عندما b = 0   ،   فإن العدد المركب a + ib = a (فبذلك $\mathrm{R}\subset \mathrm{C}$ )

و عندما  a = 0 ، فإن العدد المركب   a + ib = ib    ( وعندها يسمى عدد تخيلي)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

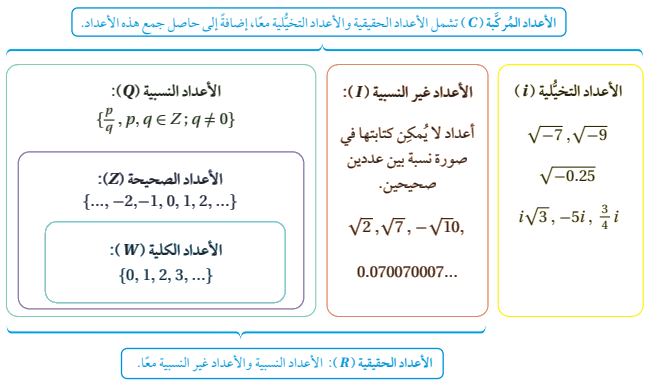
تضم مجموعة الأعداد المركبة (c) جميع هذه الأعداد.

كما تلاحظ، فإن كلاً من مجموعة الأعداد الحقيقية R ومجموعة الأعداد التخيلية هي مجموعة جزئية من مجموعة الأعداد المركبة.

وتم الاتفاق على كتابة الرمز i على يمين المضروب منه (مثل  $\frac{3}{4}i, -2i, 5i$) ، وعلى يسار المتغير أو الجذر (مثل $3 i x , i\sqrt{2} x , i\sqrt{3 }, bi$) .

مثال:

جد قيمة الجذر التربيعي الرئيس فيما يلي بدلالة i:

$$\begin{gathered} Solution: \\ a) \sqrt{-49} \\ \sqrt{-49} = \sqrt{-1\left(49\right)} \\ = \sqrt{-1}\sqrt{49} \\ = 7i \sqrt{-1}=i \\ b) \sqrt{-250} \\ \sqrt{-250 } = \sqrt{\left(25\right)(-1)\left(5\right)} \\ = 5i\sqrt{5} \end{gathered}$$             

 لاحظ أن:   

                $$\begin{gathered} {\left(i\right)}^4 = {\left(i^2\right)}^2 = {(-1)}^2 = 1 \\ {\left(i\right)}^3= {\left(i\right)}^2\left(i\right) = -1i = -i \end{gathered}$$      باستخدام خاصية القوة.

---

مثال:

جد ناتج كل مما يلي في أبسط صورة: 

$$\begin{gathered} 1) \sqrt{-12} . \sqrt{-75} \\ Solution: \\ \sqrt{-12} . \sqrt{-75} = i\sqrt{12}. i \sqrt{75} \\ =i^2\sqrt{12\left(75\right)} \\ =(-1)\sqrt{900} =-30 \end{gathered}$$             

---

$$\begin{gathered} 2) 4i\sqrt{-9} \\ Solution: \\ 4i \sqrt{-9} = 4i(i\sqrt{9}) \\ = 4i(3i) \\ =12 i^2 \\ =12(-1)=-12 \end{gathered}$$                 

---

$$\begin{gathered} 3) {\left(i\right)}^{83} \\ Solution: \\ {\left(i\right)}^{83} = {\left(i^2\right)}^{41} . {\left(i\right)}^1 \\ = {(-1)}^{41}i =-i \end{gathered}$$                

---

يتساوى العددان المركبان  a + ib , c+id إذا و فقط إذا كان a = c , b = d

اي أن: الجزءان الحقيقان متساويان، و الجزءان التخيليان متساويان.

مثال:

إذا كان $4+i(y-2) = (x+1) +i(2x+2y)$ ، فجد قيمة كل من y , x الحقيقتين:

 $$\begin{gathered} Solution: \\ 4 +i(y-2) = (x+1) +i(2x+2y) \\ Re=Re \\ 4 = x+ 1 \Rightarrow x = 3 \\ Im = Im \\ y -2 = 2x + 2y \\ y - 2 = 6 +2y \Rightarrow y = -8 \end{gathered}$$                

---

مرافق العدد المركب  z = a+ib  هو العدد المركب  $\overline{z} = a-ib$ .

و يمكن تمثيل العدد المركب$z = 2+3i$  في المستوى الإحداثي في صورة زوج مرتب (a,b)، أو صورة المتجه <a,b>

حيث يسمى: المستوى الإحداثي: المستوى او مستوى T 

و المحور الأفقي: المحور الحقيقي  Re ، و المحور الرأسي: المحور التخيلي  Im

فالعدد المركب $z = 2+3i$  يمثل على المستوى المركب بإحدى الصورتين:

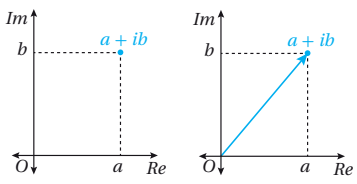
أما مرافقه $\overline{z} = 2-3i$   فهو انعكاس للعدد $z = 2+3i$   في المحور الحقيقي Re.

لاحظ أن: ناتج ضرب العددين المركبين z و  $\overline{ z}$ هو:  

 $$\begin{gathered} z.\overline{z} = (a+ib)(a-ib) \\ = (a^2 - {\left(i\right)}^2{\left(b\right)}^2) + iab - iab \\ = a^{{}^2}- (-1)b^2 = a^2+b^2\ge 0 \end{gathered}$$
لأن a, b أعداد حقيقية.

مثال:

مثل كلاً من الأعداد المركبة التالية و مرافقه بيانياً في المستوى المركب:

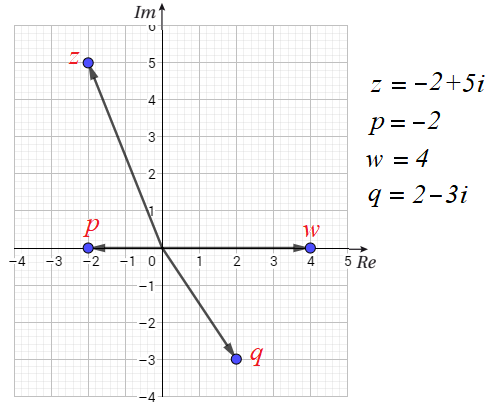
ملاحظة: التمثيل يكون بمتجهات.

إذا كان  $z = a +ib$  هي الصورة القياسية للعدد المركب z:

 مقياس العدد المركب z:

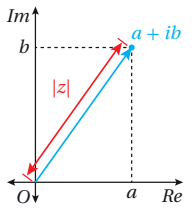       هو المسافة بين النقطة  $(a,b)$  و نقطة الأصل $(0 , 0)$ في المستوى المركب،

       و هو طول المتجه$<a, b>$و يرمز له بالرمز |z| أو  r

        و بالرموز   $r= z=\sqrt{a^2 + b^2}$

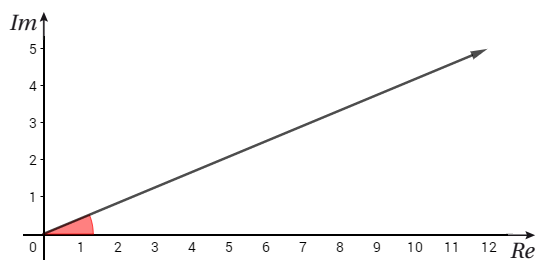
السعة الرئيسة للعدد المركب z:

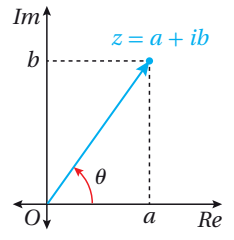       هي الزاوية  (بالراديان) و التي تقع في الفترة  و المحصورة بين المحور الحقيقي الموجب و المتجه $<a, b>$ .

       و يرمزلها بالرمز $Arg\left(z\right)$

 

 

 

سعة العدد المركب: ويرمز لها بالرمز $arg\left(z\right)$  ، حيث:

$arg\left(z\right) = Arg\left(z\right) +2\pi n :\hspace{0.17em}\mathrm{n} = 0,\pm 1 , \pm 2, ...$

 و عندما  n = 0 ، فإن arg (z) = Arg(z)

و للاختصار، تشير كلمة (السعة) إلى ( السعة الرئيسية) هنا 

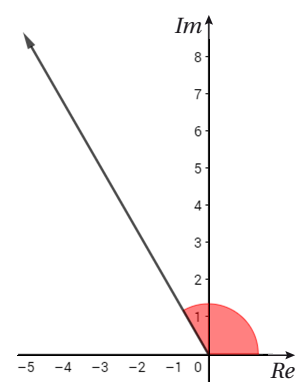
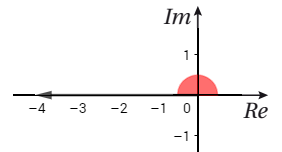
و يمكن إيجاد سعة العدد المركب اعتماداً على الربع الذي يقع فيه:

بفرض أن a , b أعداد حقيقية موجبة:

 

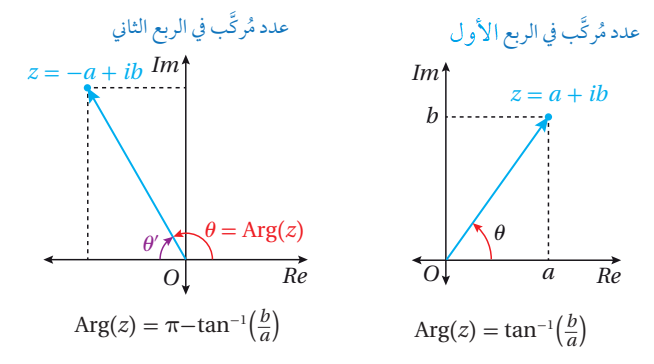
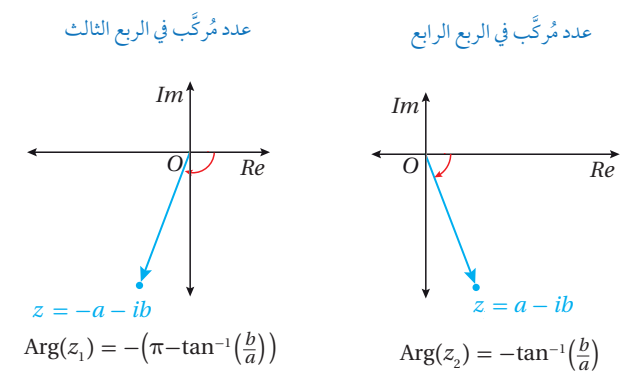
إذا كان  $z= a+ ib$ ، فإن: $Arg\left(z\right) = \theta$   هي سعة العدد المركب z
 $r=\left|z\right|$  هو مقياس العدد المركب  z

فالصورة المثلثية للعدد المركب z هي:  $z = r(cos \theta + i sin\theta )$

و تترك الإجابة على هذه الصورة دون حساب   $cos \theta , sin\theta$

مثال :

 اكتب كل عدد من الأعداد التالية بالصورة المثلثية( استخدم الآلة الحاسبة عند الحاجة، و قرب الزاوية الى اقرب منزلتين عشريتين) 

                     $$\begin{gathered} 1) z = 12 + 5i \\ Solution: \\ r = |z| = \sqrt{{12}^2+5^2} = 13 \\ \theta = Arg(z) = {\tan }^{-1}(\frac{5}{12}) \\ \theta \approx .39 rad \\ z = 13(\cos (0.39) + i \sin (0.39)) \end{gathered}$$             

---

   $$\begin{gathered} 2) z=-5 + 5i\sqrt{3} \\ Solution: \\ r = |z|= \sqrt{{(-5)}^2 +{\left(5\sqrt{3}\right)}^2}= 10 \\ \theta = Arg(z) = \pi - ta{n}^{-1}(\frac{5\sqrt{3}}{5}) \\ = \pi - ta{n}^{-1}(\sqrt{3}) \\ =\pi -\frac{\pi }{3} = \frac{2\pi }{3}rad \\ z = 10(cos\left(\frac{2\pi }{3}\right) + i sin\left(\frac{2\pi }{3}\right)) \end{gathered}$$               

---

   $$\begin{gathered} 3) z=-3-3i \\ Solution: \\ r = |z| = \sqrt{{(-3)}^2+{(-3)}^2} = 3\sqrt{2} \\ \theta = Arg(z) = -(\pi -ta{n}^{-1}\left(\frac{3}{3}\right)) \\ = -(\pi -ta{n}^{-1}\left(1\right)) \\ = -(\pi - \frac{\pi }{4}) = -\frac{3\pi }{4} \\ z = 3\sqrt{2}(cos\left(\frac{-3\pi }{4}\right)+i sin \left(\frac{-3\pi }{4}\right)) \end{gathered}$$            

---

              $$\begin{gathered} 4) z= -4 \\ Solution: \\ r = |z| = \sqrt{{(-4)}^2} = 4 \\ \theta = Arg(z) =\pi - ta{n}^{-1}(\frac{0}{4}) = \pm \pi \\ -\pi <Arg(z)\le \pi \Rightarrow Arg(-4i) = \pi \\ z = 4(cos\pi +i sin\pi ) \end{gathered}$$           

---

      $$\begin{gathered} 5) z=-2i \\ Solution: \\ r\mathit{ }\mathit{=}\mathit{ }\mathit{|}z\mathit{|}\mathit{ }\mathit{=}\mathit{ }\sqrt{{\mathit{(}\mathit{-}\mathit{2}\mathit{)}}^{\mathit{2}}}\mathit{=}\mathit{ }\mathit{2}\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ }\mathit{ } \\ \theta \mathit{ }\mathit{=}\mathit{ }Arg\mathit{(}z\mathit{)}\mathit{ }\mathit{=}\mathit{-}\mathit{ }ta{n}^{\mathit{-}\mathit{1}}\mathit{(}\frac{\mathit{2}}{\mathit{0}}\mathit{)}\mathit{ }\mathit{=}\mathit{ }\mathit{-}\frac{\pi }{\mathit{2}} \\ z\mathit{ }\mathit{=}\mathit{ }\mathit{2}\mathit{(}cos\mathit{\left(}\frac{\mathit{-}\mathit{\pi }}{\mathit{2}}\mathit{\right)}\mathit{+}\mathit{ }i\mathit{ }sin\mathit{\left(}\frac{\mathit{-}\mathit{\pi }}{\mathit{2}}\mathit{\right)} \\ z\mathit{ }\mathit{=}\mathit{ }\mathit{2}\mathit{\left(}cos\mathit{\right(}\frac{\mathit{\pi }}{\mathit{2}}\mathit{)}\mathit{-}\mathit{ }i\mathit{ }sin\mathit{(}\frac{\mathit{\pi }}{\mathit{2}}\mathit{)} \end{gathered}$$           

---