الاقترانات المتشعبة

فكرة الدرس : تعرّف الاقتران المُتشعب ، وتمثيله بيانيًا، وتحديد مجاله ومداه.

يُسمى الاقتران المُعرّف بقواعد مختلفة لأجزاء مجاله اقترانًا متشعبًا. فالاقتران المتشعب هو اقتران يدمج بين قاعدتي اقترانين أو أكثر.

 

مثال1 : إذا كان $f\left(x\right) = \{\begin{array}{l}\mathrm{x} + 4 , \mathrm{x} < -1\\ -2\mathrm{x} , \mathrm{x} \ge -1\end{array}$ ، فأجيب عن الأسئلة الآتية :

1) أحدد مجال f(x).

ألاحظ أنّ الاقتران f(x) معرف بقاعدتين هما :

• x + 4   : تُستخدم لحساب قيم الاقتران عندما تكون 1- > x

•  - 2x :  تُستخدم لحساب قيم الاقتران عندما تكون  1- ≤ x

إذن مجال الاقتران f(x) هو الفترة (¥ , ¥-)

 

2) أجد قيمة f(-6).

العدد ( -6 ) ينتمي للفترة $(-\infty , -1)$  ، إذن استخدم القاعدة الأولى :

القاعدة الأولى : x + 4   f(x) =   

تعويض (x = -6)         ==>         f(-6) = -6 + 4   = -2

 

3) أجد قيمة f(-1).

العدد (1-) ينتمي للفترة $[-1 , \infty )$ ، إذن استخدم القاعدة الثانية :

القاعدة الثانية :  f(x) = - 2x

تعويض (x = -1)        ==>           f(-1) = -2 (-1) = 2

 

4) أجد قيمة f(0).

العدد ( 0  ) ينتمي للفترة $[-1 , \infty )$ إذن استخدم القاعدة الثانية :

القاعدة الثانية : f(x) = - 2x  

تعويض (x = 0)        ==>           f(0) = -2 (0) = 0

 

5) أمثل الاقتران f(x) ، وأحدد مداه.

 • تمثيل  f(x) = x + 4 ، عند 1- > x

إيجاد قيمة الاقتران عند طرف مجاله؛ أي عندما x = -1 ، وكذلك عند قيمة اخرى تنتمى لمجاله، ولتكن  x = -2

-2	-1	x
2	3	Y = x + 4
(-2,2)	(-1,3)	(x,y)

 

 

 

 

 

 

 

عيّن النقطة (3, 1-) والنقطة (2 , 2-) في المستوى الإحداثي، وصل بينهما بخط مستقيم.

عند النقطة (3, 1-) نضع دائرة مُفرغة لأن  x = -1 ، لا تنتمي لمجال القاعدة الأولى في الاقتران.

 

• تمثيل  f(x) = - 2x  ، عند 1- ≤x

إيجاد قيمة الاقتران عند طرف مجاله؛ أي عندما x = -1  وكذلك عند قيمة اخرى تنتمى لمجاله، ولتكن  x = 0

0	-1	x
0	2	Y = - 2x
( 0,0)	(-1,2)	(x,y)

 

 

 

 

 

 

 

عيّن النقطة (2, 1-) والنقطة (0 ,0 ) في المستوى الإحداثي، وصل بينهما بخط مستقيم.

عند النقطة (2, 1-) نضع دائرة مُظللة؛ لأن  x = -1  تنتمي لمجال القاعدة الثانية في الاقتران.

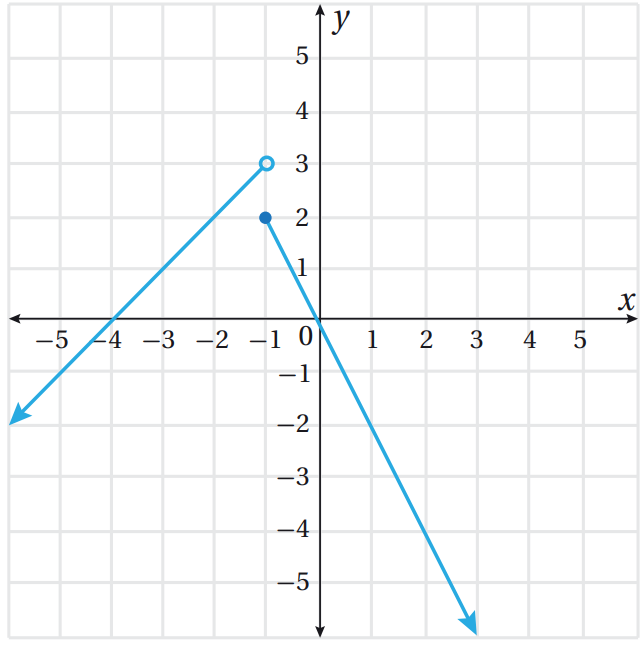
من التمثيل البياني للاقتران؛ فإن القيم التي يأخذها y  تنتمي للفترة¥ , 3)  (- ؛ أي أنّ مدى الاقتران هو ¥ , 3) (- 

---

مثال 2 : أكتب قاعدة الاقتران المتشعب الممثل بيانيًا في الشكل المجاور.

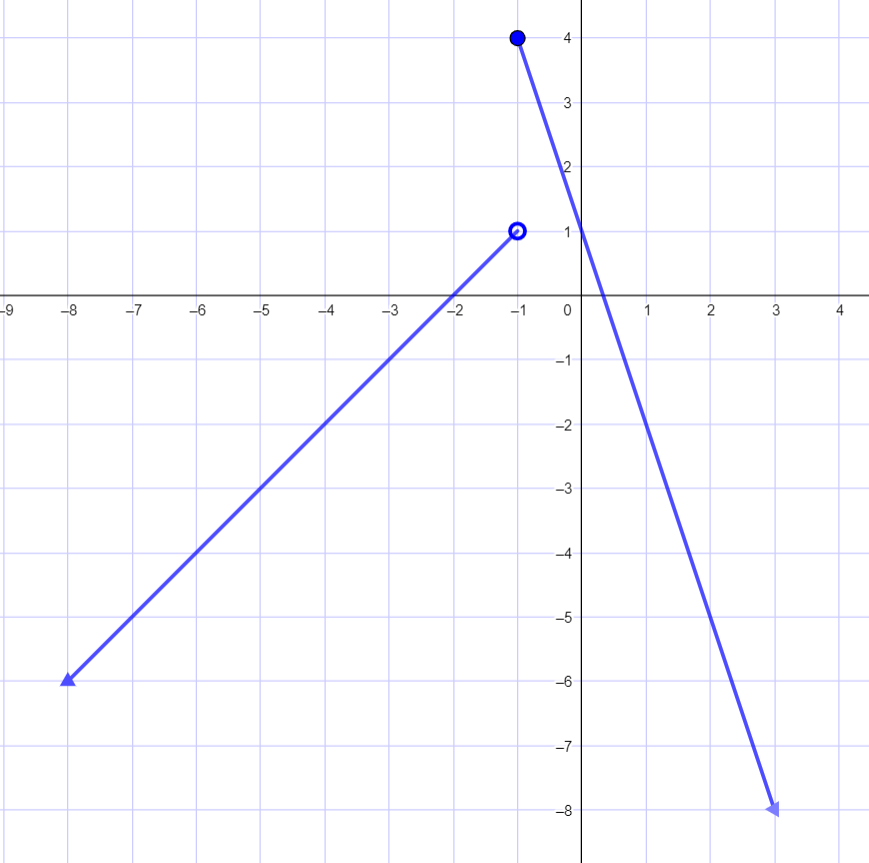الحل :  

أكتب الاقتران الذي يُمثل كل جزء في التمثيل البياني :

الخطوة 1 : أكتب قاعدة الاقتران الذي يُمثل الجزء الأيسر من التمثيل البياني ، وهو شعاع يمر بالنقطتين :$(-3 , -1) , (-2 , 0)$

وميله : $m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-1 - 0}{-3 -- 2} = \frac{-1}{-1}=1$ 

 

ثم ، نكتب معادلة الخط المستقيم بصيغة الميل والنقطة ، وهي : $\mathbf{y}\mathbf{ }\mathbf{–}\mathbf{ }{\mathbf{y}}_{\mathbf{1}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{m}\mathbf{(}\mathbf{x}\mathbf{ }\mathbf{–}\mathbf{ }{\mathbf{x}}_{\mathbf{1}}\mathbf{)}$  ، ولتكن النقطة (0 , 2-)

إذن؛y – 0  =  1 (x – –2)      (بتعويض النقطة والميل في المعادلة)

ويُمكن إعادة كتابتها في صورة  : f(x) = x + 2  

 

أما وجود دائرة غير مظللة عند النقطة (1 , -1) فيعني أن هذه القاعدة تُقابل الفترة (1- , ¥-) من مجال الاقترانf(x)   ، أي  :  -1  >  x 

 

الخطوة 2 : أكتب قاعدة الاقتران الذي يُمثل الجزء الأيمن من التمثيل البياني ، وهو شعاع يمر بالنقطتين :

 $(0 , 1) , (1 , -2)$

وميله : $m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-2 - 1}{1 - 0} = \frac{-3}{1}=-3$

 

بما أن الشعاع يقطع المحور y   عند 1 ، إذن b = 1  ، ومعادلته بصيغة الميل والمقطع هي : $\mathit{y}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{m}\mathit{x}\mathbf{ }\mathbf{+}\mathit{b}$

و (بتعويض الميل والمقطع) في المعادلة:   y = -3x + 1

ويمكن إعادة كتابتها على الصورة f(x) = -3x + 1  

 

أما وجود دائرة مظللة عند طرف الشعاع الذي يبدأ بالنقطة (4 , -1) ، فيعني أن هذه القاعدة تُقابل الفترة $[-1 و \infty )$  من مجال الاقتران  f(x) ، أي :  -1  ≤  x 

إذن ، قاعدة هذا الاقتران هي :  $f\left(x\right) = \left\{\begin{array}{l}x + 2 , x < -1\\ -3x + 1 , x \ge -1\end{array}\right.$

---

 

مثال 3 : يتقاضى مندوب مبيعات راتبًا شهريًا مقداره 450 دينار، وعمولة بنسبة 2% لأول 2000 دينار من مبيعاته الشهرية، وإذا زادت مبيعاته على 2000 دينار يأخذ عمولة بنسبة 3% مما يزيد على 2000 دينار، اكتب اقترانًا مُتشعبًا لحساب الدخل الشهري لهذا المندوب.

الحل :

افرض مبيعات المندوب =x    دينار

إذن يأخذ المندوب:   0.02 x+  450    ،   إذا كان   2000  x  ≤

ويأخذ المندوب:         

450 (الراتب)   +   40 (نسبته عن أول 2000)   +    0.03 (x – 2000) (نسبته عن المبيعات التي تزيد عن 2000 ).

 وذلك عندما x   >  2000     ،  وبالتبسيط  :  

490 + 0.03 (x - 2000) = 490 + 0.03 x - 60 = 430 + 0.03 x

إذن الاقتران المُتشعب الذي يُمثل هذا الموقف هو :  

$f\left(x\right) = \{\begin{array}{l}450 + 0.02 x , \mathrm{x} \le 2000\\ 430 + 0.03 \mathrm{x} , \mathrm{x} > 2000\end{array}$