البرهانُ الإحداثِيُّ

البرهانُ الإحداثِيُّ

Coordinate Proof

فكرةُ الدرسِ : استعمالُ الهندسةِ الإحداثيَّةِ لِبَرهَنَةِ نظرياتٍ هندسيَّةٍ.

أولًا : تمثيلُ المُضَلَّع في المُستوى الإحداثِيِّ وَتَسمِيَتُهُ

لتمثيلِ مُضَلَّعٍ في المُستوى الإحداثِيِّ، يُفَضَّلُ رسمُ أحدِ أضلاعِهِ على محورٍ إحداثِيٍّ أوْ أحدِ رؤوسِهِ على نقطةِ الأصلِ؛ وذلكَ لتسهيلِ تحديدِ إحداثياتِ بقيَّةِ رؤوسِهِ اعتمادًا على خصائصِهِ.

مثال : 

أرسُمُ في المُستوى الإحداثِيِّ المُستطيلَ ABCD ، الذي طولُهُ S وحدةً وعرضُهُ n وحدة.

الحل  :

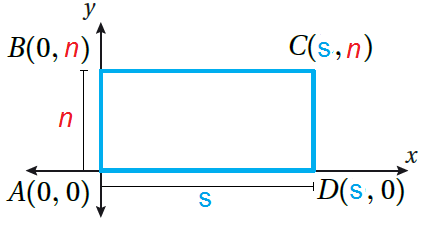أجعل زاوية المُستطيل القائمة A على نقطة الأصل ؛ لِرسُمهُ في الرّبع الأوّل. • أفترض أنَّ AD يُمَثّلُ طول المستطيل ويُساوي s وحدة، وأنَّ AB يُمَثّل عرضه ويُساوي n وحدة. • أرسُم D على المحور x. وبما أنَّ طول AD يُساوي s وحدة، فإنَّ الإحداثِيّ y للنقطة D هُو 0 ، والإحداثيّ x هُو s • أرسُمُ B على المحورِ y. وبما أنَّ طولَ AB يُساوي n وحدةً، فإنَّ الإحداثِيَّ x للنقطةِ B هُوَ 0، والإحداثِيَّ y هُوَ n • أرسُمُ الرأسَ C، بحيثُ يكونُ إحداثِيّاهُ (s , n).

 

 

 

 

 

 

 

 

 

ثانيًا : إيجادُ الإحداثياتِ المجهولةِ

يمكن تحديد إحداثيات مجهولة لرؤوس مُضَلَّع مُمَثَّل في المُستوى الإحداثِيّ، وذلك باستعمال خصائص المُضَلَّع والإحداثيات الأُخرى المعلومة.

مثال : 

أَجدُ الإحداثيات المجهولة في كلٍّ من الأشكال الآتية : 

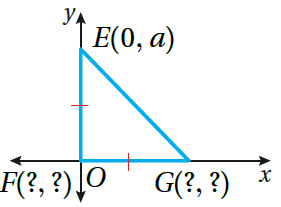بما أنَّ الرأسَ F يقعُ عندَ نقطةِ الأصلِ فإنَّ إحداثِيَّيهِ ( 0 , 0). • بما أنَّ EF ≅ FG فإنّ طولَ GF يُساوي a وحدة، وهُو يُمَثِّلُ الإحداثِيَّ x للرأسِ G • بِما أنَّ الرأس G على المحور x، فإنَّ إحداثِيَّهُ y يُساوي 0. ومنهُ، فإنَّ إحداثيّي G هُما (a , 0)
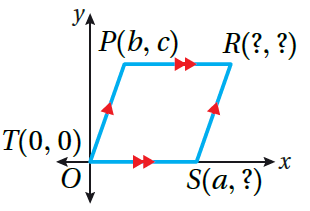بما أنَّ كلَّ ضِلعين مُتقابلين مُتوازيين فالشكل مُتوازي أضلاع. • بما أنَّ الرأس S على المحور x فإنَّ إحداثِيَّهُ y يُساوي 0. ومنهُ ، فإنَّ إحداثِيّي S هُما (a, 0). • بما أنَّ القطع المُستقيمة الأُفقيّة مُتوازية دائمًا، فإنَّ للنقطتين P و R الإحداثِيّ y نفسهُ، وبما أنَّ طولَ PR يُساوي a وحدة والإحداثيّ x للنقطةِ P هُو b، فإنَّ الإحداثيّ x للنقطة R هُو b + a . ومنهُ، فإنَّ إحداثيّي R هُما $(a+b , c)$

 

 

 

 

 

 

 

 

 

 

 

 

ثالثًا : البرهانُ الإحداثِيُّ

البرهانُ الإحداثيّ : هُو أحد أنواع البراهين، تُستعمل فيه أشكال هندسيَّة مرسومة في المُستوى الإحداثِيّ لإثبات صحَّة نظريات هندسيَّة، ويتضمَّن

أيضًا استعمالَ مُتَغَيِّرات تُمَثِّل إحداثيات رؤوس الشكل أو قياسات زواياه أوْ أضلاعهِ ؛ لضمان أنَّ النتيجةَ التي يجري برهانُها صحيحةٌ لجميعِ

الأشكال منَ النوع نفسه بغض النظر عن إحداثيات رؤوسه.

مثال : 

أكتبُ برهانًا إحداثِيًّا لأثبت أنَّهُ إذا كان الشكل الرُّباعِيّ مُتوازي أضلاع فإنَّ قُطريه يُنصف كلٌّ منهُما الآخَر.

الحل : 

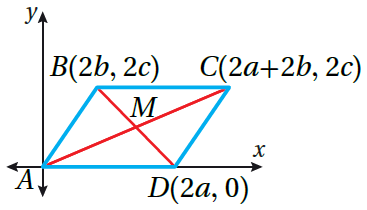الخُطوةُ 1 : أرسُمُ مُتوازي الأضلاعِ في المُستوى الإحداثِيِّ. أرسُمُ $▱ABCD$ في المُستوى الإحداثِيِّ، وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ، كما في الشكلِ المُجاورِ. الخُطوةُ 2 : أُحَدِّدُ المُعطياتِ والمطلوبَ. المُعطياتُ : • إحداثياتُ رؤوسِ $▱ABCD$   • نقطةُ تقاطعِ AC وَ BD هِيَ M المطلوبُ : إثباتُ أنَّ M نقطةُ مُنتَصَفِ AC ، ونقطةُ مُنتَصَفِ BD أيضًا. الخُطوةُ 3 : البرهانُ • أَجِدُ مُنتَصَفَ AC باستعمالِ صيغةِ نقطةِ المُنتَصَفِ.   $(\frac{2a+2a+0}{2},\frac{2c+0}{2}) = (a+b , c)$ • أَجِدُ مُنتَصَفَ BD باستعمالِ صيغةِ نقطةِ المُنتَصَفِ.    $(\frac{2a+2b}{2},\frac{2c+0}{2}) = (a+b , c)$ • بما أنَّ لكلٍّ مِنْ $\overline{AC}$ وَ $\overline{BD}$ نقطةَ المُنتَصَفِ نفسَها، ونقطةَ تقاطعِ $\overline{AC}$ وَ $\overline{BD}$ هِيَ M، فإنَّ M نقطةُ مُنتَصَفِ $\overline{AC}$ ونقطةُ مُنتَصَفِ $\overline{BD}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

رابعًا  : تصنيف الأشكال الرباعيّة باستعمال الهندسة الإحداثيّة

مراجعة المفهوم (حالاتٌ خاصَّةٌ مِنْ مُتوازي الأضلاع)

• المُستطيل مُتوازي أضلاع زواياهُ الأربع قوائمُ وقُطراهُ مُتطابقان.

• المعين مُتوازي أضلاع أضلاعُه مُتطابقة وَقُطراه مُتعامدان.

• المُربّع مُتوازي أضلاع أضلاعُه مُتطابقة وزواياه الأربع قوائمُ وأقطارُه مُتعامدة ومُتطابقة.

مثال : 

أُحَدِّدُ ما إذا كانَ $▱ ABCD$  ، الذي إحداثياتُ رؤوسِهِ $A(-1 , 3) , B(3 , 4) , C(2 , 0) , D(-2 , -1)$  ، مستطيلًا أوْ معينًا أوْ مُرَبَّعًا.

الحل : 

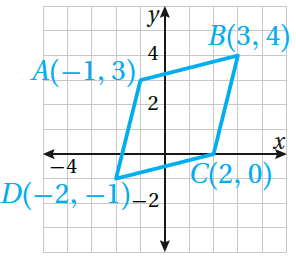الخُطوةُ 1 : أرسُمُ متوازيَ الأضلاعِ في المُستوى الإحداثِيِّ. أرسُمُ $▱ ABCD$ في المُستوى الإحداثِيِّ، كما في الشكلِ المُجاورِ.

 

 

 

 

 

 

 

الخُطوةُ 2 : أُحَدِّدُ المُعطياتِ والمطلوبَ.

المُعطياتُ: إحداثياتُ رؤوسِ $▱ ABCD$ . 

المطلوبُ : إثباتُ أنَّ $▱ ABCD$  معينٌ أوْ مُستطيلٌ أوْ مُرَبَّعٌ.

الخُطوةُ 3 : البرهانُ

إذا كانَ قُطرا مُتوازي الأضلاعِ مُتطابِقَيْنِ فإنَّهُ مُستطيلٌ، وإذا كانا مُتعامدَيْن فإنَّهُ معين، وإذا كانا مُتطابِقَين وَمُتعامِدين فإنّهُ مُرَبعٌ.

• أستعمِل صيغةَ المسافة بين نقطتين للمقارنة بين طولي القُطرين $\overline{AC}$ وَ $\overline{BD}$

  $$\begin{gathered} AC = \sqrt{(2-{(-1))}^2+{(0 + 3)}^2} = \sqrt{18} = 3\sqrt{2} \\ BD = \sqrt{(-2-{3)}^2+{(-1-4)}^2} = \sqrt{50} = 5\sqrt{2} \end{gathered}$$

بما أنَّ $3\sqrt{2} \ne 5\sqrt{2}$ فإنَّ القُطرَيْنِ ليسا مُتطابِقَيْنِ ؛ لِذا $▱ ABCD$ ليسَ مُستطيلًا ولا مُرَبَّعًا.

 

• أستعمل صيغة الميل لِتحديد ما إذا كان القُطران مُتعامدين.

ميل $\overline{AC}$	ميل $\overline{BD}$
$m = \frac{0 - 3}{2 - (-1)} = \frac{-3}{3} =-1$	$m = \frac{-1 - 4}{-2 - 3} = \frac{-5}{-5} = 1$

 

 

 

بما أنَّ حاصل ضرب المَيْلَيْنِ يُساوي 1- فإنَّ القُطرَيْنِ مُتَعامدان ؛ لِذا فإنَّ $▱ ABCD$ معين.