رياضيات9 فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 177

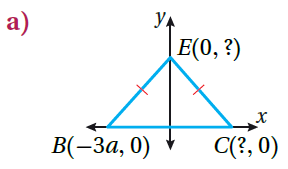
أَجِدُ الإحداثيات المجهولة في كلٍّ من الأشكال الآتية : 

النقطة C (3a , 0)  النقطة E(0 , b)
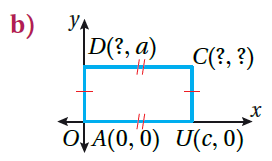
النقطة D(0 , a) النقطة C (c , a)
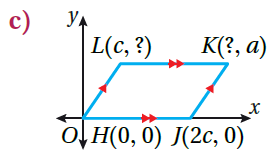
النقطة L(c , a) النقطة K(3c , a)

 

أتحقق من فهمي صفحة 179

أكتبُ برهانًا إحداثِيًّا لأثبت أنَّ القطعةَ المُستقيمةَ الواصلةَ بينَ رأسِ المُثَلَّثِ قائمِ الزاويةِ ومُنتَصَفِ الوَتَرِ تُساوي نصفَ طولِ الوَتَرِ.

الحل :

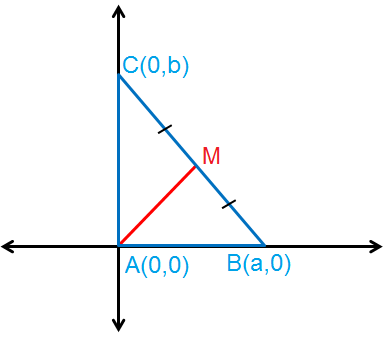
الخُطوةُ 1: أرسُمُ المُثَلَّثَ في المُستوى الإحداثِيِّ. أرسُمُ المُثَلَّثَ ABC في المُستوى الإحداثِيِّ ، وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ. الخُطوةُ 2 : أُحَدِّدُ المُعطياتِ والمطلوبَ. المعطيات  : في المثلث القائم ΔABC  ، النقطة M تقع في منتصف الوتر BC المطلوب : إثبات أنّ طول القطعة  AM = نصف طول الوتر  BC

الخُطوةُ 3 : البرهانُ 

أجد طول الوتر CB 

$CB=\sqrt[]{{(a-0)}^2+{(0-b)}^2}=\sqrt[]{{\mathbf{a}}^{\mathbf{2}}\mathbf{+}\mathbf{ }{\mathbf{b}}^{\mathbf{2}}}$

أجد إحداثيي النقطة M باستخدام صيغة منتصف قطعة مستقيمة 

$M(\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2}) = M(\frac{a + 0}{2} , \frac{0 +b}{2}) = M(\frac{a}{2},\frac{b}{2})$

أجد طول AM 

$AM=\sqrt[]{{(\frac{a}{2}-0)}^2+{(\frac{a }{2}-0)}^2}=\sqrt[]{\frac{a^2}{4}+\frac{ b^2}{4}}=\sqrt[]{\frac{a^2+b^2}{4}}\mathbf{=}\frac{\sqrt[]{{\mathbf{a}}^{\mathbf{2}}\mathbf{+}{\mathbf{b}}^{\mathbf{2}}}}{\mathbf{2}}$

---

أتحقق من فهمي صفحة 180

أكتبُ برهانًا إحداثِيًّا لأثبت أنَّهُ إذا كان في الشكل الرُّباعيّ ضلعان مُتوازيان ومُتطابقان فإنَّ الشكل الرُّباعيّ مُتوازي أضلاع.

الحل :

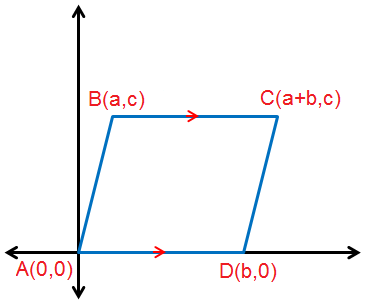
الخُطوة 1 : أرسُمُ متوازي الأضلاع في المُستوى الإحداثِيِّ. أرسُمُ متوازي الأضلاع ABCD في المُستوى الإحداثِيِّ ، وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ. الخُطوة 2 : أُحَدِّدُ المُعطياتِ والمطلوبَ. المعطيات  : الشكل ABCD المُحدد رؤوسه فيه $\stackrel{-}{AD} \left|\right| \stackrel{-}{BC}$   المطلوب : إثبات أنّ $\stackrel{-}{AB} \left|\right| \stackrel{-}{DC}$  ولهما الطول نفسه

الخُطوة 3 : البرهانُ 

أجد طول كل من AB ، DC

$AB=\sqrt[]{{(a-0)}^2+{(c-0)}^2}=\sqrt[]{{\mathbf{a}}^{\mathbf{2}}\mathbf{+}{\mathbf{c}}^{\mathbf{2}}}$

$DC=\sqrt[]{{(a+b-(b\left)\right)}^2+ {(c-0)}^2}=\sqrt[]{{\mathbf{a}}^{\mathbf{2}}\mathbf{+}{\mathbf{c}}^{\mathbf{2}}}$

أجد ميل كل من AB  ،  DC 

ميل DC	ميل AB
$m = \frac{c - 0 }{a + b - b }= \frac{c}{a}$	$m = \frac{c - 0}{a - 0} = \frac{c}{a}$

بما أن الضلعان لهما نفس الطول والميل ، إذن الشكل متوازي أضلاع. 

---

أتحقق من فهمي صفحة 181

أُحَدِّدُ ما إذا كان $▱ABCD$ ، الذي إحداثياتُ رؤوسِهِ $A(3,2) , B(4,0) , C(-2,-3) , D(-3,-1)$ مُستطيلًا أوْ معينًا أوْ مُرَبَّعًا.

الحل :

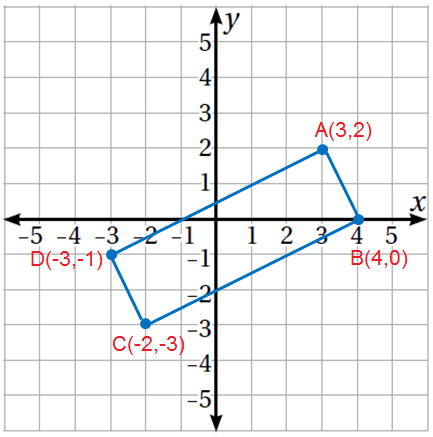
الخُطوة 1 : أرسُمُ الشكل ABCD في المُستوى الإحداثِيِّ  وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ. الخُطوة 2 : أُحَدِّدُ المُعطياتِ والمطلوبَ. المعطيات  : الشكل ABCD المُحدد رؤوسه . المطلوب : تحديد ما إذا كان الشكل ABCD مُستطيلًا أوْ معينًا أوْ مُرَبَّعًا.

الخُطوة 3 : البرهانُ 

إذا كان قُطرا الشكل مُتطابقين فإنهُ مُستطيل ، وإذا كانا مُتعامدين فإنهُ معين ، وإذا كانا مُتطابقين وَمُتعامدين فإنه مُربع.

طول القطر AC

$AC=\sqrt[]{{(3+2)}^2+{(2+3)}^2}=\sqrt[]{\mathbf{50}}$

طول القطر DB

$DB=\sqrt[]{{(4+3)}^2+{(0+1)}^2}=\sqrt[]{\mathbf{50}}$

إذن القطران متطابقان 

أجد ميل كل من القطرين  : 

ميل القطر DB	ميل القطر AC
$m = \frac{-1 - 0}{-3 - 4} = \frac{1}{7}$	$m = \frac{2 + 3}{3 + 2} = 1$

 

 

 

إذن القطران متطابقان وغير متعامدان ؛ فالشكل مستطيل . 

---

أسئلة أتدرب وأحل المسائل 

أرسُمُ كُلًّ مِنَ المُضَلَّعاتِ الآتيةِ في المُستوى الإحداثِيِّ ، مُحَدِّدًا إحداثياتِ رؤوسِ كلٍّ منها :

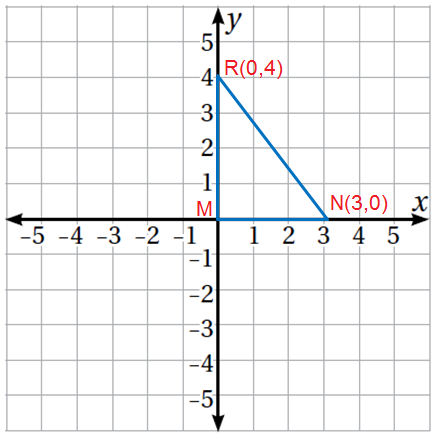
1) المُثَلَّثُ قائمُ الزاويةِ RMN ، الذي طولُ$\overline{MN }$ فيهِ يُساوي 3 وحداتٍ، وطولُ$\overline{MR }$يُساوي 4 وحداتٍ.

الحل :

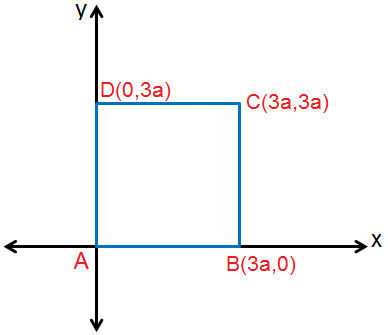
2) المُرَبَّعُ ABCD ، الذي طولُ ضِلعِهِ 3a .

الحل :

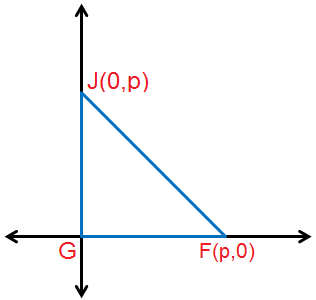
3) المُثَلَّثُ قائمُ الزاويةِ مُتطابِقُ الضِّلعَيْنِ JGF ، الذي طولُ كلٍّ مِنْ ساقَيْهِ p وحدةً.

الحل :

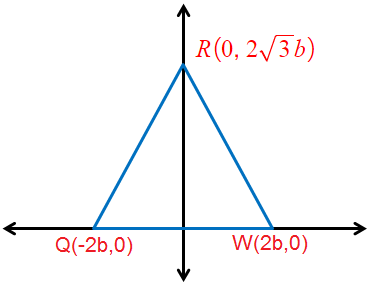
4) المُثَلَّثُ مُتطابقُ الأضلاعِ QWR ، الذي طولُ ضلعِهِ 4b .

الحل : 

---

 

أَجِدُ الإحداثياتِ المجهولةَ في كلٍّ مِنَ الأشكالِ الآتيةِ : 

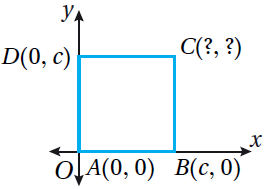
5) مُرَبَّعٌ	6) مُثَلَّثٌ	7) مُرَبَّعٌ
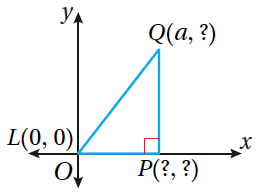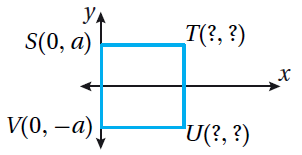C(c,c)	P(a,0)   ,   Q(a,b)	T(2a,a)          U(2a , -a)

 

 

 

 

 

 

 

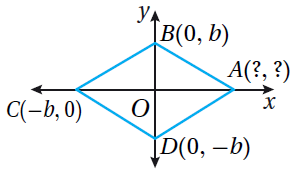
8) مُتوازي أضلاعٍ	9) معينٌ	10) مُستطيلٌ
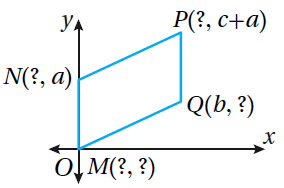m(0,0)   ,   N(0,a)  ,  P(b ,c) , Q(b,c)	A(b,0)	G(0 , 2b)  ,  F(5b,2b)

أكتبُ برهانًا إحداثِيًّا لأثبت كُلًّ ممّا يأتي :

11) إذا كانَ الشكلُ الرُّباعِيُّ مُتوازِيَ أضلاعٍ فإنَّ أضلاعَهُ المُتقابِلَةَ مُتطابقةٌ.

الحل :

• أرسُمُ متوازي الأضلاع ABCD في المُستوى الإحداثِيِّ ، وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ. • المُعطياتِ والمطلوبَ. المعطيات  : الشكل ABCD المُحدد رؤوسه فيه كل ضلعين متقابلين متوازيين   المطلوب : إثبات أنّ كل ضلعين متقابلين في الشكل متطابقين.

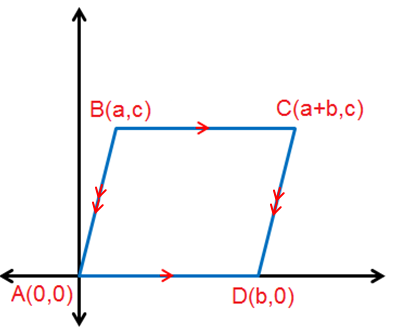البرهانُ 

أجد طول الضلعين المتقابلين AB , DC

$AB=\sqrt[]{{(a-0)}^2+{(c-0)}^2}=\sqrt[]{{\mathbf{a}}^{\mathbf{2}}\mathbf{+}{\mathbf{c}}^{\mathbf{2}}}$

$DC=\sqrt[]{{(a+b-(b\left)\right)}^2+{(c-0)}^2}=\sqrt[]{{\mathbf{a}}^{\mathbf{2}}\mathbf{+}{\mathbf{c}}^{\mathbf{2}}}$

أجد طول الضلعين المتقابلين AD , BC

$AD=\sqrt[]{{(b-0)}^2+{(0-0)}^2}=\sqrt[]{{\mathbf{b}}^{\mathbf{2}}}$

$BC=\sqrt[]{{(a+b-a)}^2+{(c-c)}^2}=\sqrt[]{{\mathbf{b}}^{\mathbf{2}}}$

---

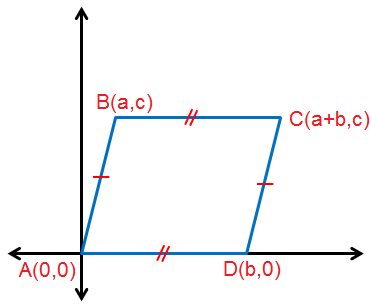
12) إذا كانَ كلُّ ضِلعَيْنِ مُتقابِلَيْنِ في الشكلِ الرُّباعيِّ مُتطابِقَيْنِ فإنَّهُ مُتوازي أضلاعٍ.

الحل :

• أرسُمُ متوازي الأضلاع ABCD في المُستوى الإحداثِيِّ ، وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ. • المُعطياتِ والمطلوبَ. المعطيات  : الشكل ABCD المُحدد رؤوسه فيه كل ضلعين متقابلين متطابقين    المطلوب : إثبات أنّ كل ضلعين متقابلين في الشكل متوازيين

البرهانُ 

أجد ميلي كل ضلعين متقابلين قإذا كان تساوى الميلين فإنّ الضلعين متوازيين  

ميل الضلع BC	ميل الضلع AD
$m = \frac{c -c}{a+b-a} = 0$	$m = \frac{0 - 0}{b - 0} = 0$

 

ميل الضلع DC	ميل الضلع AB
$m = \frac{c - 0}{a+b-b} = \frac{c}{a}$	$m = \frac{c - 0}{a - 0} = \frac{c}{a}$

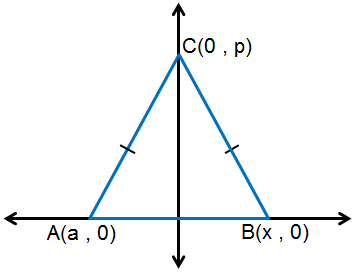
13) العمودُ النازلُ مِنْ رأسِ المُثَلَّثِ المتطابقِ الضِّلعَيْنِ إلى القاعدةِ يُنَصِّفُ القاعدةَ.

الحل :

• أرسُمُ المثلث متطابق الضلعين ABC  في المُستوى الإحداثِيِّ ، وَأُحَدِّدُ إحداثياتِ كلٍّ مِنْ رؤوسِهِ. • المُعطياتِ والمطلوبَ. المعطيات  : الشكل ABC  المُحدد رؤوسه فيه AC = BC   المطلوب : إثبات أنّ العمودُ النازلُ مِنْ رأسِ المُثَلَّثِ إلى القاعدةِ يُنَصِّفُ القاعدةَ أي a = x

البرهانُ 

$AC=\sqrt[]{{(a-0)}^2+{(0-p)}^2}=\sqrt[]{{\mathrm{a}}^2+{\mathrm{p}}^2}$

$CB=\sqrt[]{{(x-0)}^2+{(0-p)}^2}=\sqrt[]{{\mathrm{x}}^2+{\mathrm{p}}^2}$

$\sqrt[]{{\mathrm{a}}^2+{\mathrm{p}}^2}=\sqrt[]{{\mathrm{x}}^2+{\mathrm{p}}^2}$

${\mathrm{a}}^2+{\mathrm{p}}^2={\mathrm{x}}^2+{\mathrm{p}}^2$

$\Rightarrow \left|a\right|=\left|x\right|$

---

14) أستعمِلُ المعلوماتِ المُعطاةَ على الشكلِ المُجاورِ، لأثبت باستعمالِ البرهانِ الإحداثِيِّ أنَّ .ΔDEC ≅ ΔBOC

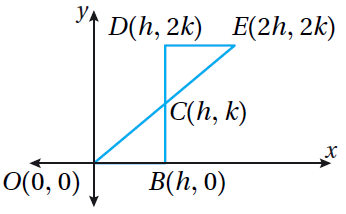الحل :

أطول أضلاع المثلث BOC

$OB=|0-h|=h$

$BC=\sqrt[]{{(h-h)}^2+{(k-0)}^2}=\sqrt[]{k^2}$

$CO=\sqrt[]{{(0-h)}^2+{(0-k)}^2}=\sqrt[]{h^2+k^2}$

 

أطول أضلاع المثلث DEC

$DE=|2h-h|=h$

$DC=\sqrt[]{{(h-h)}^2+{(2k-k)}^2}=\sqrt[]{k^2}$

$CE=\sqrt[]{{(2h-h)}^2+{(2k-k)}^2}=\sqrt[]{h^2+k^2}$

---

15) أستعمِلُ المعلوماتِ المُعطاةَ على الشكلِ المُجاورِ، لأثبت باستعمالِ البرهانِ الإحداثِيِّ أنَّ .EG ≅ FH

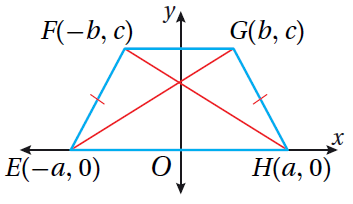الحل:

$FH=\sqrt[]{{(a+b)}^2+{(0-c)}^2}=\sqrt[]{{\mathbf{(}\mathbf{a}\mathbf{+}\mathbf{b}\mathbf{ }\mathbf{)}}^{\mathbf{2}}\mathbf{+}{\mathbf{\left(}\mathbf{c}\mathbf{\right)}}^{\mathbf{2}}}$

$EG=\sqrt[]{{(-a-b)}^2+{(0-c)}^2}=\sqrt[]{{(-a-b)}^2+{\left(c\right)}^2}=\sqrt[]{(-1{(a+b))}^2+c^2}=\sqrt[]{{\mathbf{(}\mathbf{a}\mathbf{+}\mathbf{b}\mathbf{)}}^{\mathbf{2}}\mathbf{+}{\mathbf{\left(}\mathbf{c}\mathbf{\right)}}^{\mathbf{2}}}$

---

16) في الشكلِ المُجاورِ، إذا كانَ PQ ≅ RQ ، وكانَتْ M نقطةَ مُنتَصَفِ PQ وَ N نقطةَ مُنتَصَفِ RQ ، فَأُثبِتُ باستعمالِ البرهانِ الإحداثِيِّ أنَّ PN ≅ RM .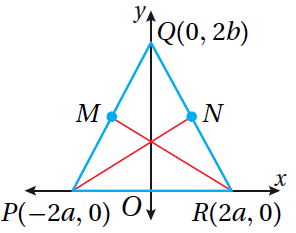

الحل:

$M=(\frac{0 - 2a}{2},\frac{2b + 0}{2})=M(-a,b)$

$RM=\sqrt[]{{(2a+a)}^2+{(0-b)}^2}=\sqrt[]{{\left(3a\right)}^2+{(-b)}^2}=\sqrt[]{{\left(3a\right)}^2+b^2}$

 

$N=(\frac{0+2a}{2},\frac{2b+0}{2})=N(a,b)$

$PN=\sqrt[]{{(-2a-a)}^2+{(0-b)}^2}=\sqrt[]{{(-3a)}^2+{(-b)}^2}=\sqrt[]{{\left(3a\right)}^2+b^2}$

---

أُحَدِّدُ ما إذا كانَ $▱ JKLM$ المُعطاةُ إحداثياتُ رؤوسِهِ في كلٍّ ممّا يأتي ، معينًا أوْ مُستطيلً أوْ مُرَبَّعًا : 

 

17) J(-4 , 2) , K(0 , 3) , L(1, -1) , M(-3 , -2) 

أجد طول كل من القطرين MK ،  JL

$MK=\sqrt[]{{(-3-0)}^2+{(-2-3)}^2}=\sqrt[]{\mathbf{34}}$

$JL=\sqrt[]{{(-4-1)}^2+{(2+1)}^2}=\sqrt[]{\mathbf{34}}$

أجد ميل كل من القطرين 

ميل MK  : $m=\frac{-2 -3}{-3 - 0}=\frac{5}{3}$

ميل JL  :  $m=\frac{-1-2}{1+4}=-\frac{ 3}{5}$

بما أنّ القطرين متطابقين ومتعامدين فالشكل مربع . 

---

 18) J(-2 , 7) , K(7 , 2) , L(-2 , -3) , M(-11 , 2)

$MK=\sqrt[]{{(-11-7)}^2+{(2-2)}^2}=\mathbf{18}$

$JL=\sqrt[]{{(-2+2)}^2+{(7+3)}^2}=\mathbf{10}$

ميل MK  : $m=\frac{2-2}{-11-7}=0$  الميل  = صفر إذن القطر أفقي 

ميل JL  :   $m=\frac{7+3}{-2+2}=\frac{10}{0}$  الميل غير معرف ، إذن القطر رأسي 

إذن القطران متعامدان وغير متطابقان ؛ فالشكل معين .

---

 19) J(5 , 0) , K(8  , -11) , L(-3 , -14) , M(-6 , -3) 

$MK=\sqrt[]{{(8+6)}^2+{(-11+3)}^2}=\mathbf{2}\sqrt[]{\mathbf{65}}$

$JL=\sqrt[]{{(5+3)}^2+{(0+14)}^2}=\mathbf{2}\sqrt[]{\mathbf{65}}$

ميل MK  : $m=\frac{-11+3}{8+6}=-\frac{14}{14}=-1$

ميل JL  :  $m=\frac{0+14}{5+3}=\frac{14}{8}=\frac{7}{4}$

إذن القطران متطابقان وغير متعامدان ؛ إذن الشكل مستطيل.

---

20) J(-1 , 4) , K(-3 , 2) , L(2 , -3) , M(4 , -1)

 $MK=\sqrt[]{{(-3-4)}^2+{(2+1)}^2}=\sqrt[]{\mathbf{58}}$

$JL=\sqrt[]{{(-1-2)}^2+{(4+3)}^2}=\sqrt[]{\mathbf{58}}$

ميل MK  :  $m=\frac{-1-2}{ 4+3}=-\frac{3}{7}$

ميل JL  :  $m=\frac{4+3}{-1-2}=-\frac{7}{3}$

القطران متطابقان وعير متعامدان ؛ إذن الشكل مستطيل 

---

مهاراتُ التفكيرِ العُليا

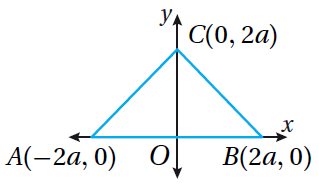
21) تبريرٌ: أصَُنفُِّ ΔABC ، المرسومَ في المُستوى الإحداثِيِّ المُجاورِ، بحسبِ أضلاعِهِ وزواياهُ، مُبَرِّرًا إجابتي.

الحل:

$AC=\sqrt[]{{(-2a-0)}^2+{(0-2a)}^2}=\sqrt[]{{(-2a)}^2+{(-2a)}^2}=\sqrt[]{8a^2}$

$CB=\sqrt[]{{(0-2a)}^2+{(2a-0)}^2}=\sqrt[]{{(-2\mathrm{a})}^2+{\left(2\mathrm{a}\right)}^2}=\sqrt[]{8a^2}$

$AB=\sqrt[]{{(-2a-0)}^2+{(0-2a)}^2}=\sqrt[]{{(-2\mathrm{a})}^2+{(-2\mathrm{a})}^2}=\sqrt[]{8a^2}$

مثلث متطابق الأضلاع ومتطابق الزوايا. 

---

22) أكتشف الخطأ : تقول شذا إنَّ الشكل الرُّباعيّ PQRS ، الذي إحداثيات رؤوسه $P(0 , 2) , Q(3 , -4) , R(1 , -5) , S(-2 , 1)$  متوازي أضلاعٍ وليس مُستطيلًا، وتقول ضُحى إنَّهُ مُستطيل. أيُّ الإجابتين صحيحة؟ أُبَرِّرُ إجابتي.

الحل:

إجابة ضحى صحيحة فالشكل مستطيل وكل مستطيل هو متوازي أضلاع زواياه الأربع قوائم وقطراه متطابقان ، بينما إجابة شذى غير صحيحة لأنه متوازي أضلاع وزواياه قوائم وقطراه متطابقان فالشكل مستطيل.   

---

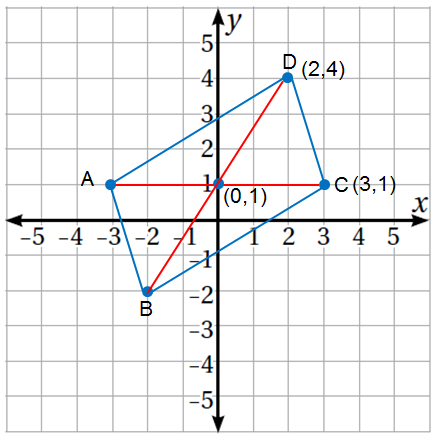
23) تَحَدّ : مُتوازي أضلاع أحدُ رُؤوسِه النقطةُ (4 , 2) والرأس الآخَر النقطة (1 , 3) ونقطةُ تقاطع قُطرَيْه (1 , 0). أجَِدُ بَقِيَّةَ رُؤوسِه.

الحل:

النقطة (1،0) تقع منتصف القطرين ، أجد النقطة A ، والنقطة B من صيغة منتصف قطعة مستقيمة  

النقطة A  $(0,1)=(\frac{x+3}{2},\frac{y+1}{2})$ $\frac{x+3}{2}=0\Rightarrow x=-3$ $\frac{y+1}{2}=1\Rightarrow y=1$

النقطة B  $(0,1)=(\frac{x+2}{2},\frac{y+4}{2})$ $\frac{x+2}{2}=0\Rightarrow x=-2$ $\frac{y+4}{2}=1\Rightarrow y=-2$

أسئلة كتاب التمارين 

أرسُمُ كُلًّ مِنَ المُضَلَّعاتِ الآتيةِ في المُستوى الإحداثِيِّ ، مُحَدِّدًا إحداثياتِ رُؤوسِ كلٍّ منها :

1) مُثَلَّثٌ مُتطابِقُ الضِّلْعَيْنِ طولُ قاعدتِهِ 2b وارتفاعُهُ 2c . 

الحل :

    

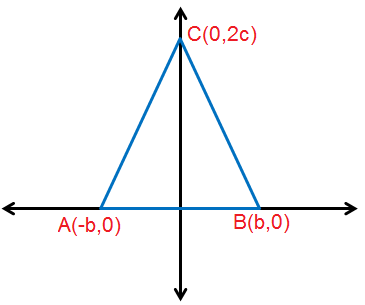
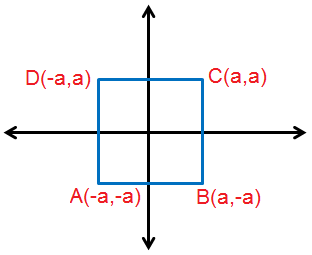
2) مُرَبَّعٌ طولُ ضِلعِهِ 2a ، ويلتقي قُطراهُ في نقطةِ الأصلِ.

الحل :

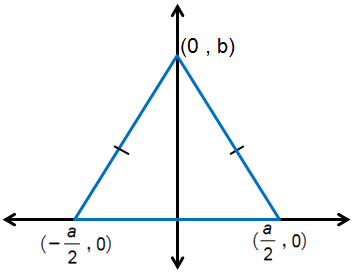
3) مُثَلَّثٌ مُتطابِقُ الأضلاعِ طولُ قاعدتِهِ a.

الحل :

---

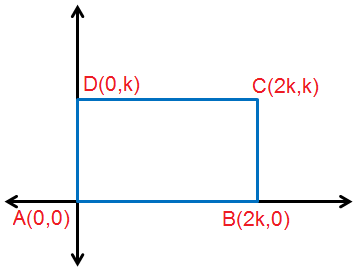
4) مُستطيلٌ طولُهُ 2k وحدةً وعرضُهُ k وحدةً.

الحل :

---

أَجِدُ الإحداثياتِ المجهولةَ في كلِّ شكلٍ مِنَ الأشكالِ الآتيةِ :  

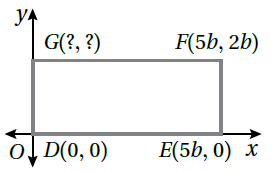
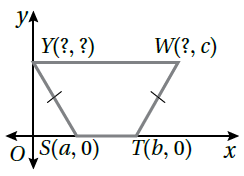
5) مُستطيلٌ	6) شبهُ مُنحَرِفٍ	7) مُرَبَّعٌ
G(0,2b)	Y(0,c)  ,  W(a+b,c )	B(a,a)

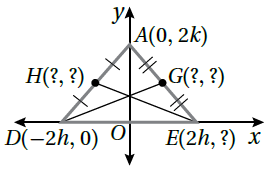
8) مُثَلَّثٌ	9) مُثَلَّثٌ	10) مُتوازي أضلاعٍ
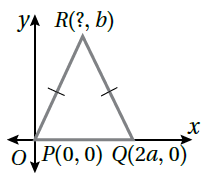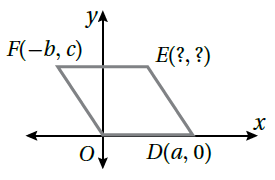H(-h,k)  ,   G(h,k)	R(a,b)	E(a-b,c)

11) أستعمِلُ المعلوماتِ المُعطاةَ في الشكلِ الآتي ؛ لأثبت باستعمالِ البرهانِ الإحداثِيِّ أنَّ ΔODB ≅ ΔBDC

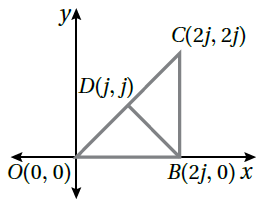
الحل : 

DB ضلع مشترك بين المثلثين 

أضلاع المثلث ODB

$OB=|2j-0|=\mathbf{2}\mathit{j}$

$OD=\sqrt[]{{(j-0)}^2+{(j-0)}^2}=\sqrt[]{\mathbf{2}{\mathbf{j}}^{\mathbf{2}}}$

 

أضلاع المثلث BDC

$CB=|2j-0|=\mathbf{2}\mathit{j}$

$CD=\sqrt[]{{(2j-j)}^2+{(2j-j)}^2}=\sqrt[]{\mathbf{2}{\mathbf{j}}^{\mathbf{2}}}$

إذن المثلثين متطابقين. 

---

12) أستعمِلُ المعلوماتِ المُعطاةَ في الشكلِ الآتي ؛ لأثبت باستعمالِ البرهانِ الإحداثِيِّ أنَّ ΔOPQ ≅ ΔQRO

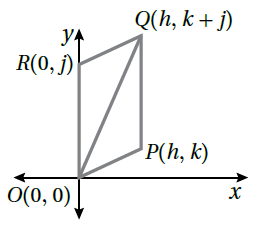
الحل : 

QO ضلع مشترك بين المثلثين 

أضلاع المثلث OPQ

$OP=\sqrt[]{{(h-0)}^2+{(k-0)}^2}=\sqrt[]{{\mathbf{h}}^{\mathbf{2}}\mathbf{+}{\mathbf{k}}^{\mathbf{2}}}$

$PQ=\sqrt[]{{(h-h)}^2+{(K+j-k)}^2}=\sqrt[]{{\mathbf{j}}^{\mathbf{2}}}$

 

أضلاع المثلث QRO

$OR=\sqrt[]{{(0-0)}^2+{(j-0)}^2}=\sqrt[]{\mathbf{ }{\mathbf{j}}^{\mathbf{2}}}$

$RQ=\sqrt[]{{(h-0)}^2+{(K+j -j)}^2}=\sqrt[]{{\mathbf{h}}^{\mathbf{2}}\mathbf{+}{\mathbf{k}}^{\mathbf{2}}}$

إذن المثلثين متطابقين. 

---