رياضيات فصل أول

التحليلُ بإخراج العامل المشترك الأكبر

مفاهيم عامة :

الصورة التحليلية :  كتابة المقدار الجبري على صورة حاصل ضرب  أعداد أولية ومتغيرات كلٌ منها مرفوع للأس 1 فمثلاً :

 

 

 

 

العدد الأولي : هو عدد طبيعي أكبر من 1 ، ولا يقبل القسمة إلا على نفسه وعلى العدد 1 فمثلاً : 2,3,5,7,11,13,17  تعتبر أعداداً أولية.

العاملَ المشتركَ الأكبرَ (ع. م. أ)  لعددَينِ أَوْ أكثرَ يساوي ناتجَ ضربِ العواملِ الأوليةِ المشتركةِ بينَها، ويمكنُ أيضًا إيجادُ العاملِ المشتركِ الأكبرِ لحدَّينِ جبريَّينِ أَوْ أكثرَ بطريقةٍ مشابهةٍ .
 

---

مثال 1 : أجدُ العاملَ المشتركَ الأكبرَ للحدَّينِ الجبريَّينِ في كلٍّ ممّا يأتي:

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{12}{\mathit{y}}^{\mathbf{2}}\mathbf{ }\mathbf{,}\mathbf{18}\mathit{y}$

 

الحل : نكتب كل حد جبري بالصورة التحليلية ، ثم نحدد العوامل الأولية المشتركة ونضربها ببعضها ... توضيح  :

 

 

$\mathbf{3}\mathbf{\times }\mathbf{2}\mathbf{\times }\mathit{y}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{6}\mathit{y}$

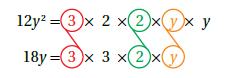
إذاً العامل المشترك الأكبر  بين الحدين هو 6y.

---

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{20}{\mathit{z}}^{\mathbf{2}}\mathit{d}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{10}{\mathit{z}}^{\mathbf{5}}\mathit{d}\mathit{c}\mathbf{ }$

الحل : نكتب كل حد جبري بالصورة التحليلية ، ثم نحدد العوامل الأولية المشتركة ونضربها ببعضها ... توضيح  :

 

 

$\mathbf{5}\mathbf{\times }\mathbf{2}\mathbf{\times }\mathit{z}\mathbf{\times }\mathit{z}\mathbf{\times }\mathit{d}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{10}{\mathit{z}}^{\mathbf{2}}\mathit{d}$

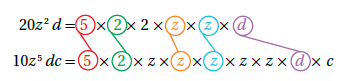
إذاً العامل المشترك الأكبر  بين الحدين هو $\mathbf{10}{\mathit{z}}^{\mathbf{2}}\mathit{d}$

---

تذكر :  نستخدم خاصية التوزيع لضرب حد جبري أو عدد في مقدار جبري .

مثال :   $$\begin{gathered} \mathbf{3}\mathit{x}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{8}\mathbf{)}\mathbf{=}\mathbf{3}\mathit{x}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{+}\mathbf{3}\mathit{x}\mathbf{\left(}\mathbf{8}\mathbf{\right)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{3}{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{24}\mathit{x} \end{gathered}$$

والعملية العكسية  التي نقوم بها لإعادةِ كتابةِ مقاديرَ جبريةٍ على صورةِ حاصلِ ضربِ حدٍّ جبريٍّ في مقدارٍ جبريٍّ تكون بالتحليل ، ومن أهم طرق التحليل ، التحليل بإخراج العامل المشترك الأكبر

---

مثال 2 أحللُ كلَّ مقدارٍ جبريٍّ ممّا يأتي تحليلً كاملً:

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{6}\mathit{x}\mathbf{+}\mathbf{18}$

الحل : أولاً : نقوم بتحليل كل حد إلى عوامله الأولية ، ثم  نجد العامل المشترك الأكبر بين الحدين : 6x ,18 . كالتالي :

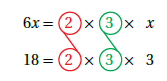
إذاً العامل المشترك الأكبر  بين الحدين هو $\mathbf{2}\mathbf{\times }\mathbf{3}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{6}$

 

ثانياً : نكتبُ كلَّ حدٍّ على صورةِ ناتجِ ضربِ العاملِ المشتركِ الأكبرِ في بقيةِ العواملِ، ثُمَّ أخرجُ العاملَ المشتركَ الأكبرَ خارجَ القوسِ. كالتالي :

$$\begin{gathered} \mathbf{6}\mathit{x}\mathbf{+}\mathbf{18}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{6}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{+}\mathbf{6}\mathbf{\left(}\mathbf{3}\mathbf{\right)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{6}\mathbf{(}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)} \end{gathered}$$

---

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{6}{\mathit{b}}^{\mathbf{2}}\mathbf{ }\mathit{k}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{8}{\mathit{k}}^{\mathbf{3}}\mathbf{ }{\mathit{b}}^{\mathbf{5}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{12}{\mathit{k}}^{\mathbf{2}}$

الحل : أولاً : نقوم بتحليل كل حد إلى عوامله الأولية ، ثم  نجد العامل المشترك الأكبر بين الحدود. كالتالي :

 

 

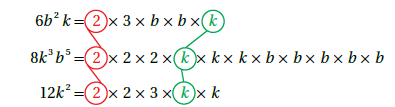
إذاً العامل المشترك الأكبر  بين الحدين هو $\mathbf{2}\mathbf{\times }\mathbf{ }\mathit{k}\mathbf{ }\mathbf{=}\mathbf{2}\mathit{k}$

 

ثانياً : نكتبُ كلَّ حدٍّ على صورةِ ناتجِ ضربِ العاملِ المشتركِ الأكبرِ في بقيةِ العواملِ، ثُمَّ أخرجُ العاملَ المشتركَ الأكبرَ خارجَ القوسِ. كالتالي :

$$\begin{gathered} \mathbf{6}{\mathit{b}}^{\mathbf{2}}\mathit{k}\mathbf{+}\mathbf{8}\mathbf{ }{\mathit{k}}^{\mathbf{3}}\mathbf{ }{\mathit{b}}^{\mathbf{5}}\mathbf{+}\mathbf{12}{\mathit{k}}^{\mathbf{2}}\mathbf{=}\mathbf{ }\mathbf{2}\mathit{k}\mathbf{(}\mathbf{3}{\mathit{b}}^{\mathbf{2}}\mathbf{ }\mathbf{)}\mathbf{+}\mathbf{2}\mathit{k}\mathbf{(}\mathbf{4}{\mathit{k}}^{\mathbf{2}}{\mathit{b}}^{\mathbf{5}}\mathbf{ }\mathbf{)}\mathbf{+}\mathbf{2}\mathit{k}\mathbf{\left(}\mathbf{6}\mathit{k}\mathbf{\right)} \\ \mathbf{=}\mathbf{2}\mathit{k}\mathbf{(}\mathbf{3}{\mathit{b}}^{\mathbf{2}}\mathbf{+}\mathbf{ }\mathbf{4}{\mathit{k}}^{\mathbf{2}}\mathbf{ }{\mathit{b}}^{\mathbf{5}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{6}\mathit{k}\mathbf{)} \end{gathered}$$

---

تعلم : طريقة تجميع الحدود : 

تستعمل في تحليلُ بعضِ المقاديرِ الجبريةِ الّتي تحتوي أربعةَ حدودٍ جبريةٍ أَوْ أكثرَ وذلكَ بتجميعِ الحدودِ الّتي توجدُ عواملُ مشتركةٌ بينَها، ويمكنُ أَنْ تكونَ هذهِ العواملُ المشتركةُ مقاديرَ جبريةً (ليسَتْ حدودًا فحسبُ) ، مع تحقق بعض الشروط وإليك التوضيح :

 

 

 

---

طريقة إضافية مساعدة :

هناك طريقة سهلة لإيجاد العامل المشترك الأكبر بين مجموعة حدود وهي على جزأين :

 

1- الأعداد :  نأخذ أكبر عدد يقسم يقسم كل الاعداد والمعاملات لجميع الحدود .  مثل : 

$\mathbf{8}\mathit{x}\mathbf{+}\mathbf{6}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{2}\mathbf{(}\mathbf{4}\mathit{x}\mathbf{+}\mathbf{3}\mathbf{)}$ حيث سحبنا العدد 2 لأنه أكبر عدد يقسم ال8  وال 6.

 

2- المتغيرات : نأخذ من المتغيرات المشتركة(نفس الحرف)  ، المتغيرات صاحبة الأس الأصغر . مثل : 

$\mathbf{3}{\mathit{x}}^{\mathbf{7}}\mathbf{-}\mathbf{5}{\mathit{x}}^{\mathbf{2}}\mathbf{+}\mathbf{4}{\mathit{x}}^{\mathbf{5}}\mathbf{+}\mathbf{13}{\mathit{x}}^{\mathbf{9}}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{2}}\mathbf{(}\mathbf{3}{\mathit{x}}^{\mathbf{5}}\mathbf{-}\mathbf{5}\mathbf{+}\mathbf{4}{\mathit{x}}^{\mathbf{3}}\mathbf{+}\mathbf{13}{\mathit{x}}^{\mathbf{7}}\mathbf{)}$

---

مثال 3 : أحللُ كلَّ مقدارٍ جبريٍّ ممّا يأتي تحليلاً كاملاً :

 

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{5}\mathit{a}\mathit{b}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{10}\mathit{a}\mathbf{+}\mathbf{7}\mathit{b}\mathbf{+}\mathbf{14}\mathbf{ }$

الحل : نجمّع الحدود ذات العوامل المشتركة ثم نحلل كل تجميع بإخراج العامل المشترك كالتالي : 

$$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{5}\mathit{a}\mathit{b}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{10}\mathit{a}\mathbf{+}\mathbf{7}\mathit{b}\mathbf{+}\mathbf{14}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{5}\mathit{a}\mathit{b}\mathbf{+}\mathbf{10}\mathit{a}\mathbf{)}\mathbf{+}\mathbf{(}\mathbf{7}\mathit{b}\mathbf{+}\mathbf{14}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{5}\mathit{a}\mathbf{(}\mathit{b}\mathbf{+}\mathbf{2}\mathbf{)}\mathbf{+}\mathbf{7}\mathbf{(}\mathit{b}\mathbf{+}\mathbf{2}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$

نلاحظ  أن (b+2 ) عامل مشترك بين الحدود ، لذا نسحبه كعامل مشترك :

$\mathbf{(}\mathit{b}\mathbf{+}\mathbf{2}\mathbf{)}\mathbf{(}\mathbf{5}\mathit{a}\mathbf{+}\mathbf{7}\mathbf{)}$

---

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{6}{\mathit{m}}^{\mathbf{3}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{12}\mathit{m}\mathit{n}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{m}}^{\mathbf{2}}\mathbf{ }\mathit{n}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{2}{\mathit{n}}^{\mathbf{2}}$

الحل : نجمّع الحدود ذات العوامل المشتركة ثم نحلل كل تجميع بإخراج العامل المشترك كالتالي : 

$$\begin{gathered} \mathbf{6}{\mathit{m}}^{\mathbf{3}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{12}\mathit{m}\mathit{n}\mathbf{ }\mathbf{+}\mathbf{ }{\mathit{m}}^{\mathbf{2}}\mathbf{ }\mathit{n}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{2}{\mathit{n}}^{\mathbf{2}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{6}{\mathit{m}}^{\mathbf{3}}\mathbf{-}\mathbf{12}\mathit{m}\mathit{n}\mathbf{)}\mathbf{+}\mathbf{(}{\mathit{m}}^{\mathbf{2}}\mathit{n}\mathbf{-}\mathbf{2}{\mathit{n}}^{\mathbf{2}}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{6}\mathit{m}\mathbf{(}{\mathit{m}}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathit{n}\mathbf{)}\mathbf{ }\mathbf{+}\mathit{n}\mathbf{(}{\mathit{m}}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathit{n}\mathbf{)} \end{gathered}$$

نلاحظ  أن $\mathbf{(}{\mathit{m}}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathit{n}\mathbf{)}$عاملاً مشترك بين الحدود ، لذا نسحبه كعامل مشترك :

$\mathbf{(}{\mathit{m}}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathit{n}\mathbf{)}\mathbf{(}\mathbf{6}\mathit{m}\mathbf{+}\mathit{n}\mathbf{)}$

---

ملاحظة :

عندَ تحليلِ المقاديرِ الجبريةِ، ألاحظُ أحيانًا وجودَ معكوسِ بعضِ العواملِ، فمثلا : $(x-6)$ هو معكوس $(6-x)$ لأن   :   $(6-x) =-1(x-6)$

---

مثال 4 : أحللُ كلَّ مقدارٍ جبريٍّ ممّا يأتي تحليلً كاملً:

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{2}\mathit{m}\mathbf{(}\mathbf{7}\mathit{m}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{4}\mathbf{(}\mathbf{3}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{7}\mathit{m}\mathbf{)}$

الحل : نجعل الحدود المشتركة متشابهة وذلك بتغيير صورتها كالتالي :

$\mathbf{(}\mathbf{3}\mathbf{-}\mathbf{7}\mathit{m}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{(}\mathbf{7}\mathit{m}\mathbf{-}\mathbf{3}\mathbf{)}$

$$\begin{gathered} \mathbf{2}\mathit{m}\mathbf{(}\mathbf{7}\mathit{m}\mathbf{-}\mathbf{3}\mathbf{)}\mathbf{+}\mathbf{4}\mathbf{(}\mathbf{3}\mathbf{-}\mathbf{7}\mathit{m}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{2}\mathit{m}\mathbf{(}\mathbf{7}\mathit{m}\mathbf{-}\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{4}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{(}\mathbf{7}\mathit{m}\mathbf{-}\mathbf{3}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{7}\mathit{m}\mathbf{-}\mathbf{3}\mathbf{)}\mathbf{(}\mathbf{2}\mathit{m}\mathbf{-}\mathbf{4}\mathbf{)} \end{gathered}$$

---

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{15}\mathit{x}\mathbf{-}\mathbf{5}\mathit{x}\mathit{y}\mathbf{+}\mathbf{6}{\mathit{y}}^{\mathbf{2}}\mathbf{-}\mathbf{18}\mathit{y}$

الحل : 

نجمّع االحدود ، ثم نخرج العامل المشترك من كل تجميع .

$$\begin{gathered} \mathbf{15}\mathit{x}\mathbf{-}\mathbf{5}\mathit{x}\mathit{y}\mathbf{+}\mathbf{6}{\mathit{y}}^{\mathbf{2}}\mathbf{-}\mathbf{18}\mathit{y}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{15}\mathit{x}\mathbf{-}\mathbf{5}\mathit{x}\mathit{y}\mathbf{)}\mathbf{+}\mathbf{(}\mathbf{6}{\mathit{y}}^{\mathbf{2}}\mathbf{-}\mathbf{18}\mathit{y}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{5}\mathit{x}\mathbf{(}\mathbf{3}\mathbf{-}\mathit{y}\mathbf{)}\mathbf{+}\mathbf{6}\mathit{y}\mathbf{(}\mathit{y}\mathbf{-}\mathbf{3}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$

نجعل الحدود المشتركة متشابهة وذلك بتغيير صورتها كالتالي :

$\mathbf{(}\mathit{y}\mathbf{-}\mathbf{3}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{(}\mathbf{3}\mathbf{-}\mathit{y}\mathbf{)}$

$$\begin{gathered} \mathbf{ }\mathbf{=}\mathbf{ }\mathbf{5}\mathit{x}\mathbf{(}\mathbf{3}\mathbf{-}\mathit{y}\mathbf{)}\mathbf{+}\mathbf{6}\mathit{y}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{(}\mathbf{3}\mathbf{-}\mathit{y}\mathbf{)}\mathbf{ } \\ \mathbf{ }\mathbf{=}\mathbf{ }\mathbf{(}\mathbf{3}\mathbf{-}\mathit{y}\mathbf{)}\mathbf{(}\mathbf{5}\mathit{x}\mathbf{-}\mathbf{6}\mathit{y}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$

---

مثال 5: منَ الحياةِ 
نجارةٌ: يبيّنُ الشكلُ المجاورُ لوحًا خشبيًّا دائريَّ الشكلِ طولُ نصفِ قطرِهِ 6x سنتيمتراً تتوسطُهُ مرآةٌ مربعةٌ طولُ ضلعِها 4x سنتيمتراً .  أكتبُ مقدارًا جبريًّا يمثلُ مساحةَ المنطقةِ الّتي لا تغطّيها المرآةُ مِنَ اللوحِ الخشبيِّ بدلالةِ x وأحللُ المقدارَ تحليلاً كاملً.

 

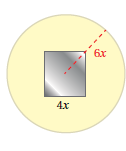
الحل : نجد مساحة الدائرة ومساحة المرآة ثم نطرح (مساحة الدائرة - مساحة المرآة )

ملاحظة :

مساحة الدائرة : $\mathit{A}\mathbf{1}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\pi r}}^{\mathbf{2}}$

مساحة المرآة (مربع) : $\mathit{A}\mathbf{2}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{S}}^{\mathbf{2}}$

أولاً : نجد مساحة المنطقة الظاهرة التي تعطيها المرآة من اللوح الخشبي بدلالة x :

$$\begin{gathered} \mathit{A}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{A}\mathbf{1}\mathbf{-}\mathit{A}\mathbf{2} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\pi r}}^{\mathbf{2}}\mathbf{-}{\mathbf{S}}^{\mathbf{2}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{\left(}\mathbf{6}\mathit{x}\mathbf{\right)}}^{\mathbf{2}}\mathbf{\pi }\mathbf{ }\mathbf{-}\mathbf{ }{\mathbf{\left(}\mathbf{4}\mathbf{x}\mathbf{\right)}}^{\mathbf{2}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{36}{\mathbf{\pi x}}^{\mathbf{2}}\mathbf{-}\mathbf{16}{\mathbf{x}}^{\mathbf{2}} \\ \mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$

ثانياً : نحلل المقدار تحليلاً كاملاً.

$$\begin{gathered} \mathbf{36}{\mathbf{\pi x}}^{\mathbf{2}}\mathbf{-}\mathbf{16}{\mathbf{x}}^{\mathbf{2}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{4}{\mathbf{x}}^{\mathbf{2}}\mathbf{\left(}\mathbf{9}\mathbf{\pi }\mathbf{\right)}\mathbf{ }\mathbf{-}\mathbf{4}{\mathbf{x}}^{\mathbf{2}}\mathbf{\left(}\mathbf{4}\mathbf{\right)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{4}{\mathbf{x}}^{\mathbf{2}}\mathbf{(}\mathbf{9}\mathbf{\pi }\mathbf{-}\mathbf{4}\mathbf{)} \end{gathered}$$

---