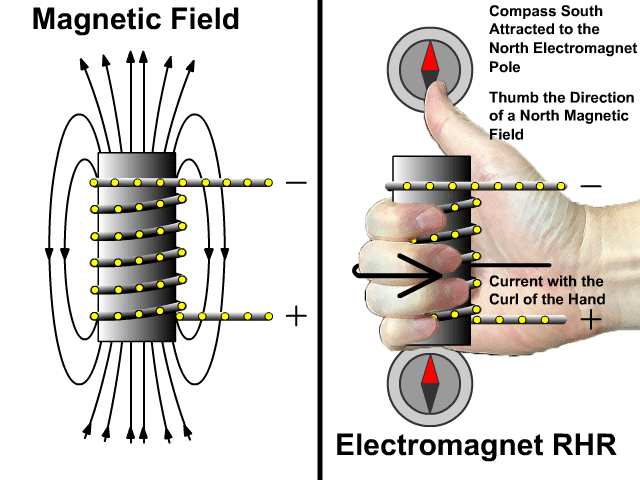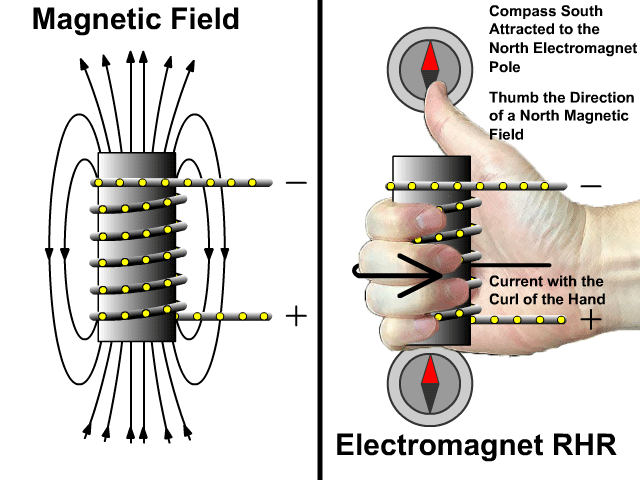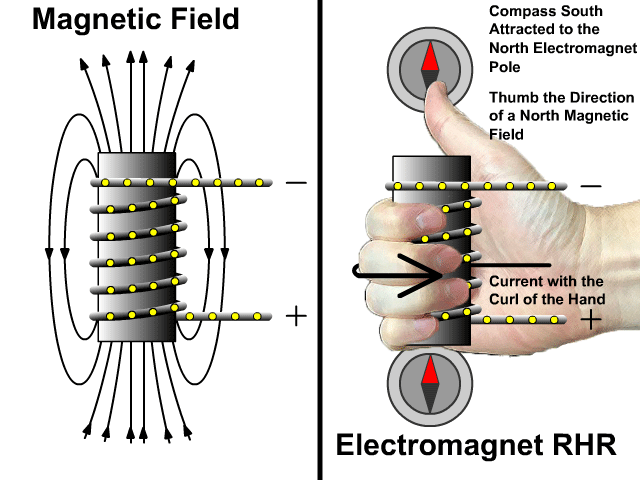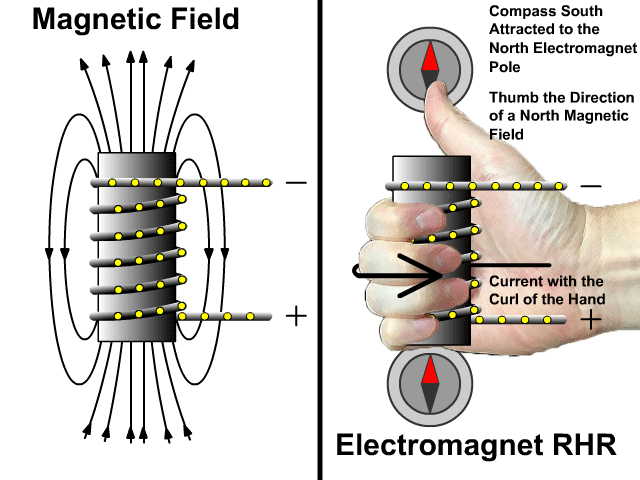
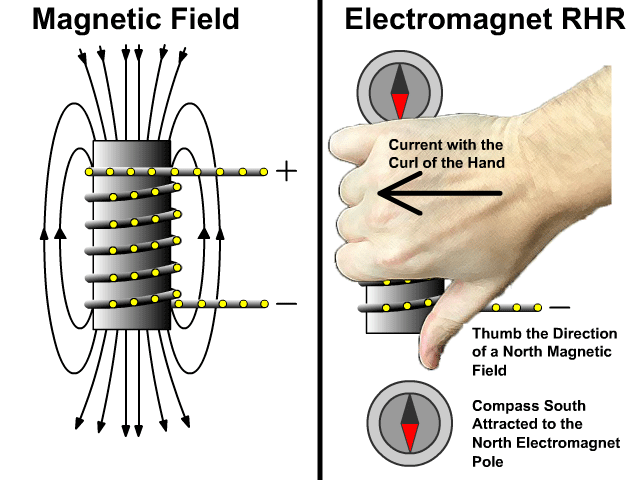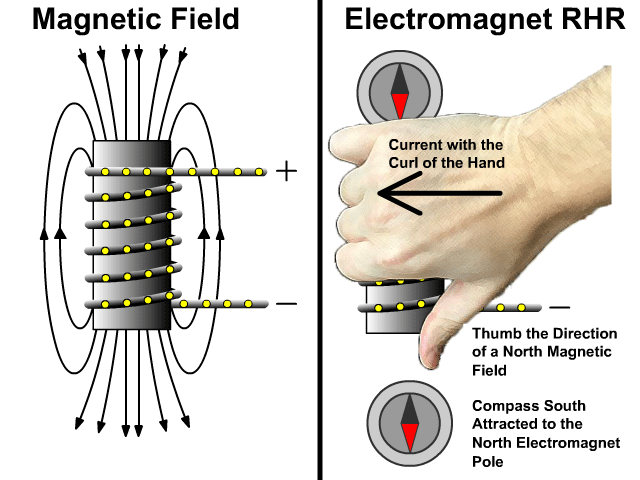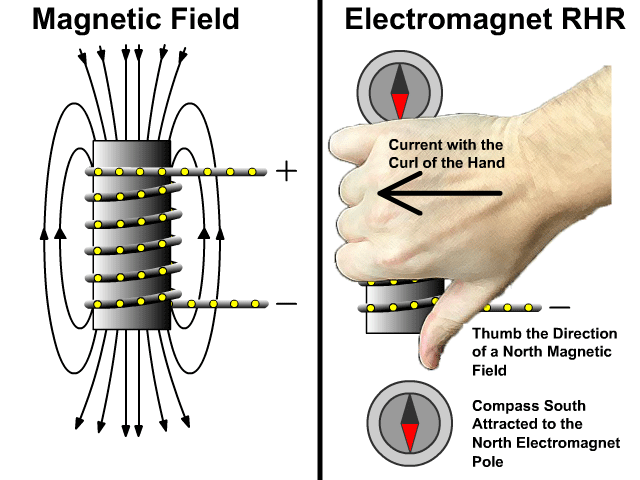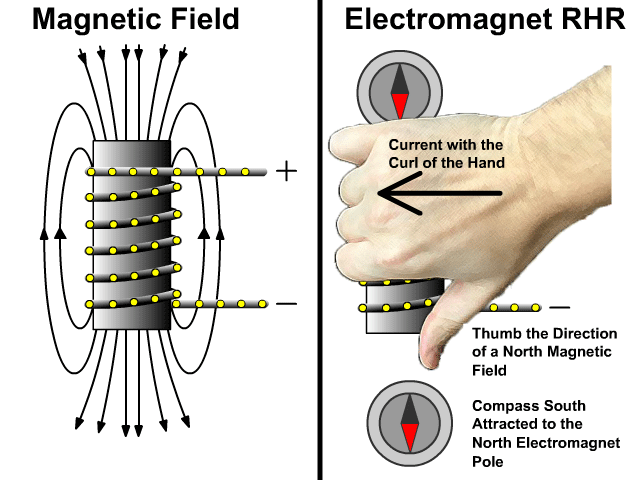
التدفق المغناطيسي والحث الكهرمغناطيسي
Magnetic Flux and Electromagnetic Induction
|
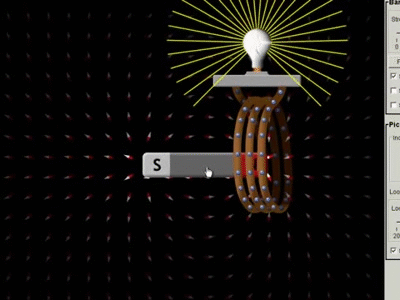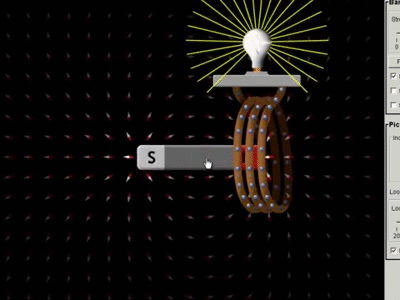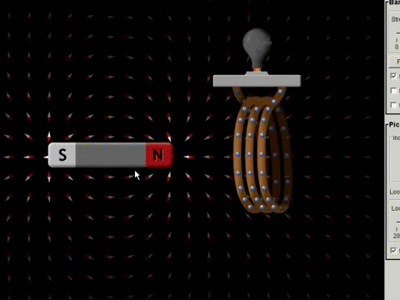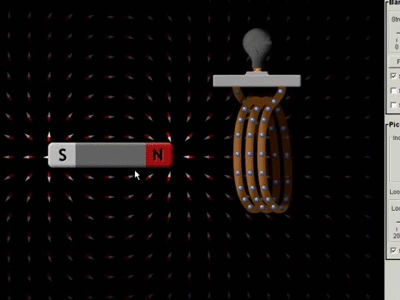
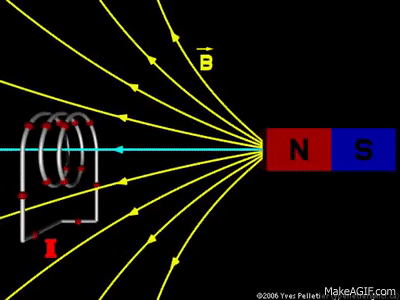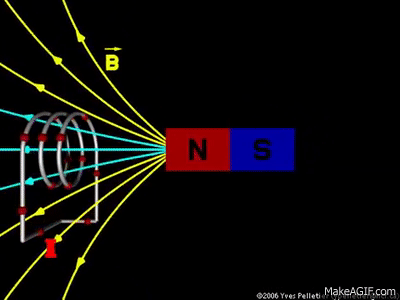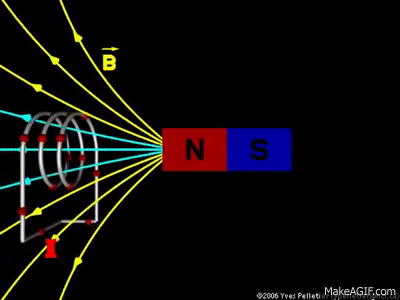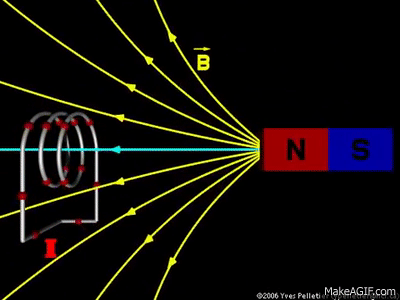
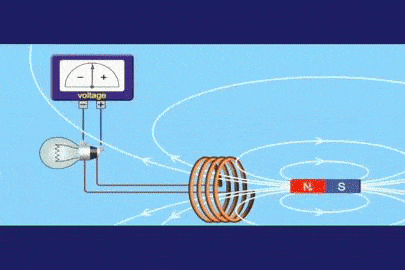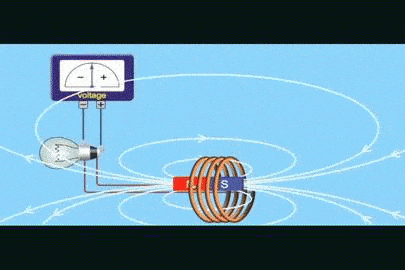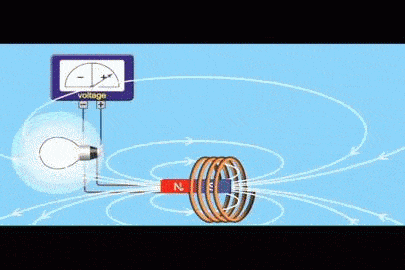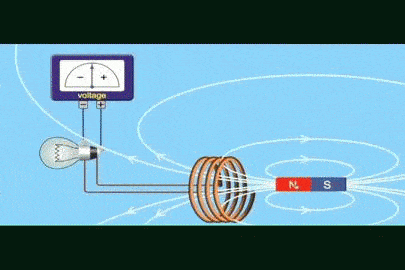
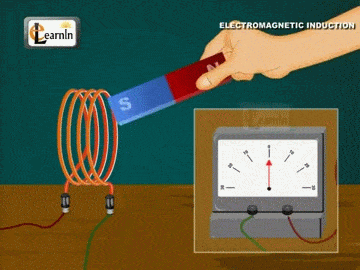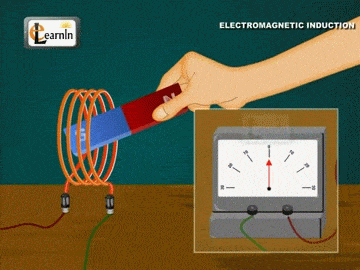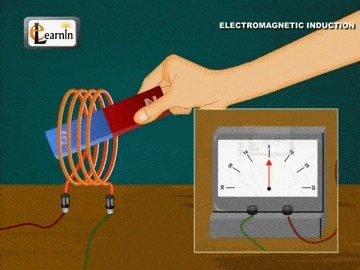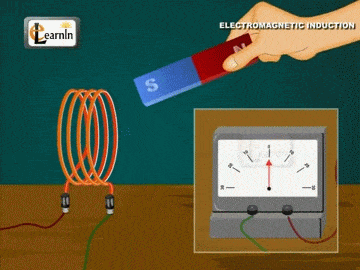
تمهيد: تحدث ظاهرة الحث الكهرومغناطيسي عند استخدام موصل ومغناطيس، ثم تحريك المغناطيس وتثبيت الموصل، أو تثبيت المغناطيس وتحريك الموصل، إذ ينتج عن ذلك التحريك تغيّر في التدفق المغناطيسي وبالتالي توليد قوة دافعة حثية عبر الملف، ويتم توليد القوة الدافعة الحثية بسبب حركة الموصل أو الملف عبر المجال المغناطيسي أو بسبب التغير في التدفق المغناطيسي،ويحدث هذا التغير إما عندما يتم وضع الموصل في مجال مغناطيسي متحرك أي عند استخدام مصدر تيار متردد (AC)، أو عندما يتحرك الموصل دائمًا في مجال مغناطيسي ثابت، وتعمل ظاهرة الحث الكهرو مغناطيسي على توليد التيار الكهربائيباستخدام المجال المغناطيسي. كما أن اكتشاف ظاهرة الحث الكهرومغناطيسي أثبت أنّه يمكن توليد تيار كهربائي باستخدام المجال المغناطيسي، ومبدأ عمل المحول الكهربائي يعتمد على ظاهرة الحث الكهرو مغناطيسي |
|
|
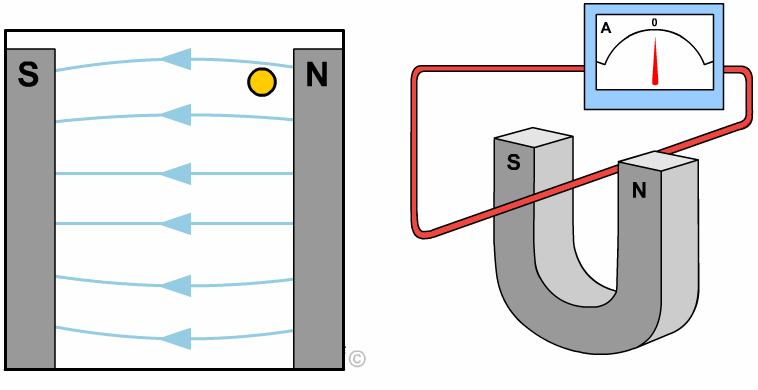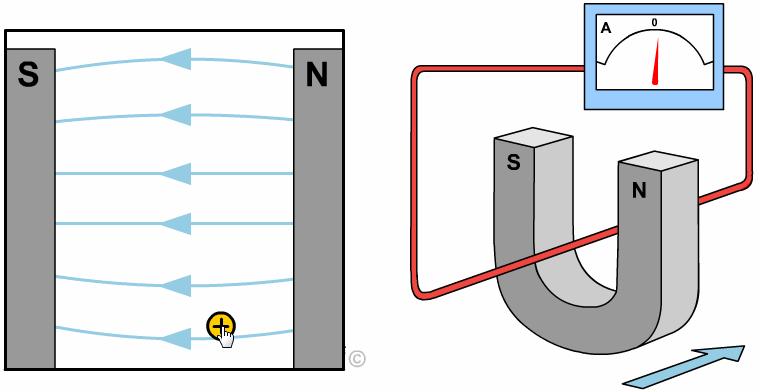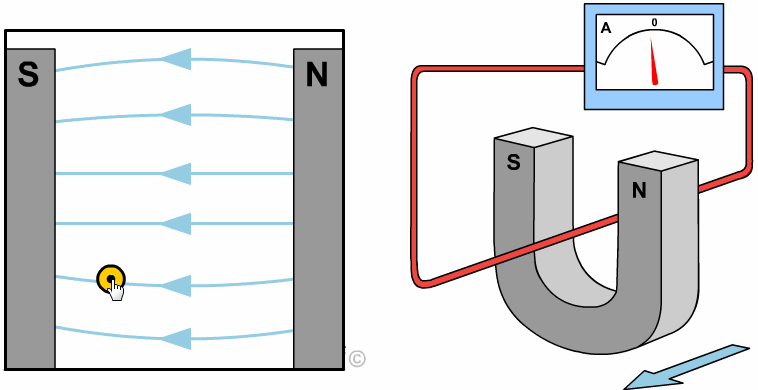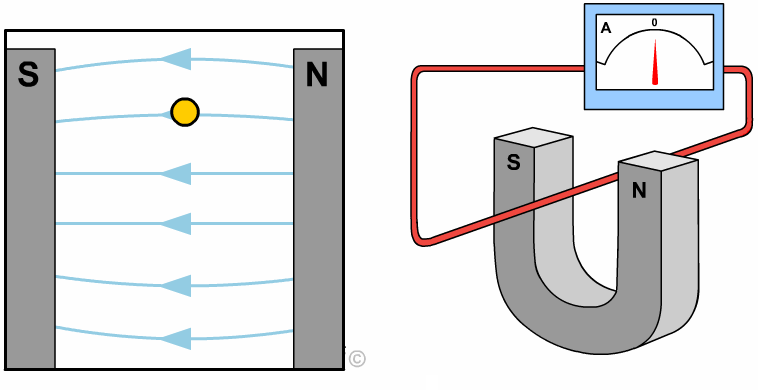
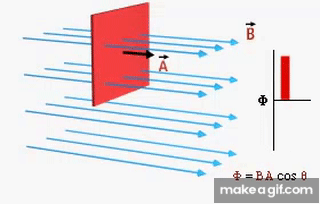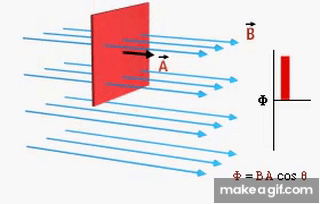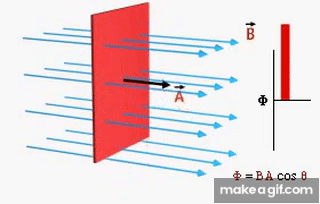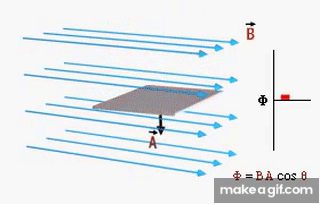
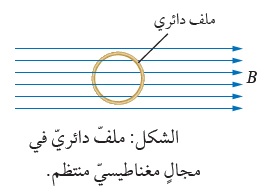
التدفق المغناطيسي Magnetic Flux من خلال التجربة السابقة أمكن توليد تيار في الملف بدون مصدر جهد (بطارية أو طاقة شمسية)،وذلك عندما يتغير عدد خطوط المجال المغناطيسي التي تخترق عموديا مساحة الملف، كما ألاحظ في المشهد الحركي المقابل،حيث يتولد تيار عندما يتغير عدد خطوط المجال المغناطيسي والتي تخترق الملف( لاحظ تغير لون الخطوط التي تخترق الملف إلى الأزرق وذلك للتوضيح فقط). مقدار المجال المغناطيسي يتناسب مع عدد خطوط المجال المغناطيسي التي تخترق عموديًّا وحدة المساحة، فإنّه يمكن التعبير عن التدفّق المغناطيسي (ΦB)رياضيًّا بأنّه ناتج الضرب القياسي لمتَّجه المجال المغناطيسي ( B) ومتَّجه المساحة ( A)، ويُعبَّر عن مقداره بالعلاقة الآتية: ΦB = B ∙ A = BA cos θ المغناطيسي ومتجه المساحة (A) التي تكون دائماً متعامدة مع السطح نحو الخارج. ومقدار متجه المساحة يساوي مقدار مساحة السطح. من العلاقة السابقة أنّ التدفّق المغناطيسي كميّة قياسيّة، يُقاس بوحدة ( T.m2 )، تسمّى ويبر ( We ) حسب النظام الدوليّ للوحدات.
|
من الشكلين في الأعلى نلاحظ أنه يمكن تغيير التدفق المغناطيسي ( ) عن طريق: 1- تغيير مقدار مساحة السطح ( A ). 2- تغيير الزاوية بين متجه المساحة العمودي على السطح واتجاه المجال المغناطيسي 3- تغيير مقدار المجال المغناطيسي الذي يخترق السطح. |
يمثل الشكل التالي سطح مغمور في مجال
مغنطيسي منتظم ، وتحرك السطح من الوضع ( 1 )
إلى الوضع ( 2 ) ثم إلى الوضع ( 3 )، وألاحظ أن عدد خطوط
المجال المغناطيسي التي تخترق مساحة سطح ( أي التدفق
المغناطيسي ( ) تتغير من وضع إلى آخر.
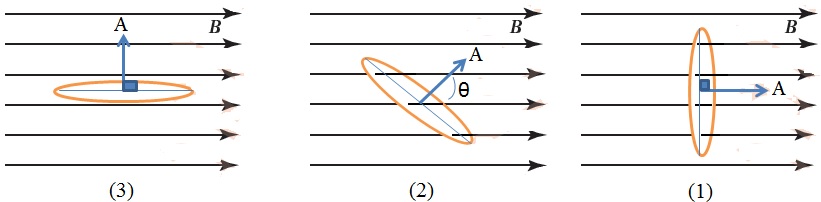
(1) ألاحظ في هذا الوضع قيمة عظمى للتدفق المغناطيسي
عندما يكون مستوي السطح متعامد مع اتجاه المجال
المغناطيسي.( )
(2) التدفق المغناطيسي عند أي زاوية بين متجهي المجال
المغناطيسي والمساحة ( )
(3) ينعدم التدفق المغناطيسي عندما يكون مستوى السطح
موازياً خطوط المجال المغناطيسي، ( )، أي عندما
يكون مستوى الملف يوازي
من ذلك أستنتج ان مقدار التدفق المغناطيسي يقل
عندما تتغير الزاوية المحصورة بين اتجاه المجال
المغناطيسي ومتجه المساحة من الصفر إلى 90o .
|
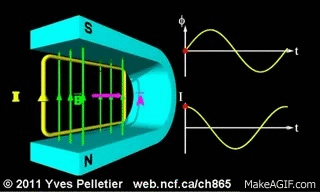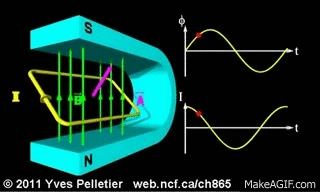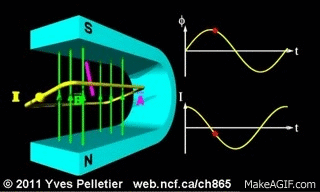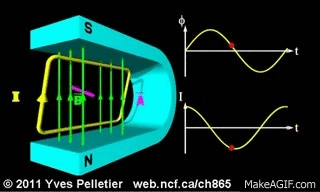
أتأمل المشهد المتحرك التالي الذي يوضح تغير التدفق المغناطيسي الذي يخترق مساحة ملف مستطيل يدور داخل مجال مغناطيسي منتظم، و تأكل الرسم البياني المرافق للتغير التدفق بصورة مستمرة مع حركة الملف.
|
 |
ومن التدفق المغناطيسي : نستنتج أن
التدفق المغناطيسي الذي يخترق عمودياً سطح ما
يعتمد على العوامل التالية:
- مقدار المجال المغناطيسي ( B )
- مقدار متجه المساحة المتعامد مع السطح
( مساحة السطح A الذي خترقه المجال المغناطيسي )
- مقدار جيب تمام الزاوية ( ) المحصورة بين اتجاه المجال
المغناطيسي ومتجه المساحة.
ويمكن تغير مقدار التدفق المغناطيسي بتغير أي من
هذه العوامل.
مثال 1:
حلقة مستطيلة أبعادها ( 2cm , 1cm)، موضوعة في مجال
مغناطيسي منتظم مقداره ( 0.4T ) على نحو ما هو موضّح في
الأشكال التالية:
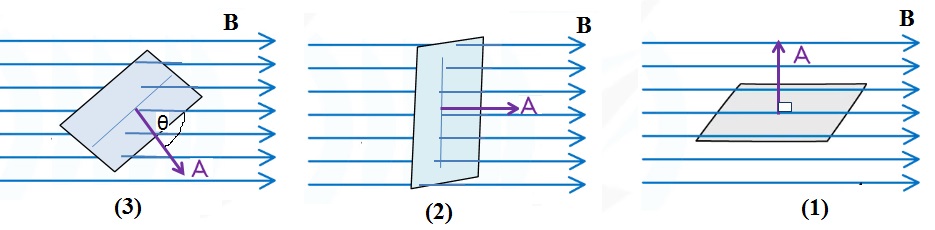
اعتماداً على ذلك أحسب مقدار ما يلي:
أ- التدفق المغناطيسي الذي خترق السطح في كل
من الوضعين (1) و (2)
ب- التغير في التدفق المغناطيسي إذا انتقلت الحلقة
من الوضع ( 1) إلى الوضع (2).وما المعنى الفيزيائي
لإشارة الجواب؟
ج- الزاوية ( ) إذا كان التدفق المغناطيسي الذي يخترق
الحلقة في الوضع (3 ) يساوي 8x10-5Wb.
الحل:
أ-
ب- التغير في التدفق المغناطيسي عند انتقال الحلقة من
الوضع ( 1) إلى الوضع (2).
والإشارة السالبة تدل على حدوث تناقص في التدفق المغناطيسي
عند الانتقال من الوضع 2 إلى الوضع 1.
ج- مقدار الزاوية في الوضع (3 ) حيث التدفق 4x10-5Wb:
مثال2:
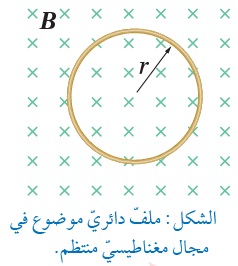
حلقة دائريّة مساحتها ( 3x10-4m2 )، موضوعة في مجال
مغناطيسي منتظم مقداره ( 120mT) على نحو ما هو موضّح
في الشكل (أ). ويوضّح الشكل(ب)منظرًا جانبيًّا للحلقة، حيث
الزاوية المحصورة بين متَّجهي المجال المغناطيسي والمساحة
تساوي 60˚ .
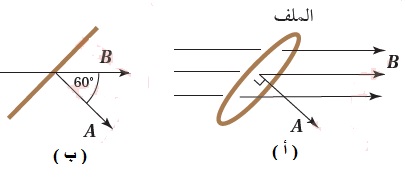
أحسب التدفّق المغناطيسيّ عبر الحلقة:
أ . على نحو ما هي موضّحة في الشكل (ب)
ب. عندما يكون مستوى الحلقة عموديًّا على اتجاه
المجال المغناطيسي.
ج. عندما يكون مستوى الحلقة موازيًا لاتجاه المجال
المغناطيسي.
الحل:
أ . الزاوية بين متّجهي المجال المغناطيسي والمِساحة ( 60˚ )،
وأحسب التدفّق المغناطيسيّ على النحو الآتي:
ΦB = BA cos θ = 120 × 1 0-3 × 3.0 × 10-4 × cos 60˚= 1.8 × 1 0-5 Wb
ب . عندما يكون مستوى الحلقة عموديًّا على اتجاه المجال
المغناطيسي تكون الزاوية بين متَّجهي المجال المغناطيسي
والمِساحة ( 0˚ )، وأحسب التدفّق المغناطيسي على النحو الآتي:
ΦB = BA cos θ = 120 × 10-3 × 3.0 × 1 0-4 × cos 0˚= 3.6 × 10-5 Wb
ج. عندما يكون مستوى الحلقة موازيًا لاتجاه المجال المغناطيسي
تكون الزاوية بين متَّجهي المجال المغناطيسيّ والمِساحة ( 90˚ )،
وأحسب التدفّق المغناطيسي على النحو الآتي:
ΦB = BA cos θ= 120 × 10-3 × 3.0 × 10-4 × cos 90˚ = 0
يكون التدفّق المغناطيسيّ صفرًا؛ لأنّ .cos 90˚ = 0
مثال3: مكعب طول ضلعه (4cm )، موضوع في مجال مغناطيسي
منتظم مقداره ( 1.5T ) على نحو ما هو موضَّح في الشكل التالي:
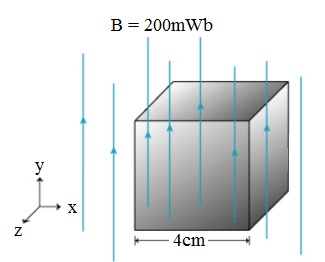
أحسب:
أ- التدفق الذي يخترق كل الوجوه الستة في المكعب,
ب- التدفّق المغناطيسيّ الكلي عبر المكعّب.
|
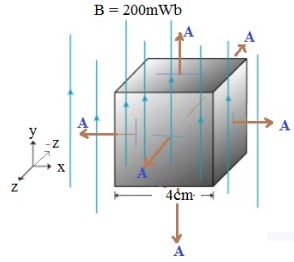
الحل: أ- الزاوية بين اتجاهي كل من المجال المغناطيسي و المساحة لكل من الأوجه الجانبية تساوي صفر ( ):
التدفق خلال الوجه العلوي للمكعب:
التدفق خلال الوجه السفلي للمكعب:
مجموع التدفق لكل من السطح العلوي والسطح السفلي:
|
 |
|
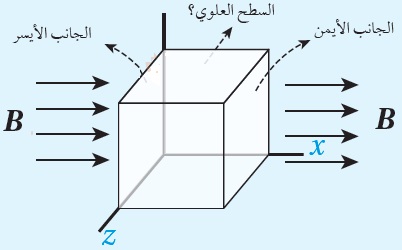
تمرين: مكعب طول ضلعه ( 2.0cm، موضوع في مجال مغناطيسي منتظم مقداره ( 1.5T) على نحو ما هو موضَّح في الشكل ( 5). أحسب التدفّق المغناطيسيّ الكلي عبر المكعّب الحل:التدفق المغناطيسي الكلي يساوي المجموع الجبري للتدفق المغناطيسي عبر كل جانب من جوانب المكعب الستة. التدفق المغناطيسي عبر أربعة جوانب يساوي صفراً؛ لأن الزاوية بين متجهي المجال المغناطيسي والمساحة ( 90˚ ) لذا يكون التدفق المغناطيسي الكلي ناتج عن المجموع الجبري للتدفق عبر كل من الجانب الأيسر ( 1 ) و الجانب الأيمن ( 2) ومساحة كل منهما A. = BAcos 180o +BAcos 0o = -BA+BA=0
|
 |
|
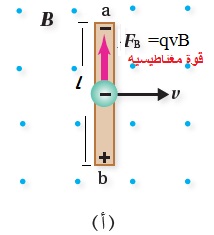
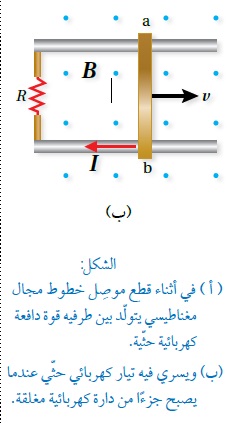
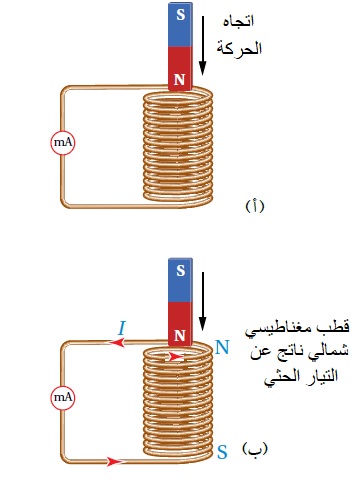
الحثّ الكهرمغناطيسيّ Electromagnetic Induction كيف يمكن تولّيد تيار كهربائي في دارة كهربائية دون وجود بطارية؟ نفذ العالمان هنري وفارادي تجارب ، ومنها أستنتج العالمان أنه يمكن توليد تيار كهربائي دون وجود بطارية في دارة مغلقة عند: 1. تحريك سلك موصل إلى الأعلى وإلى الأسفل في دارة مثل المبينة في الشكل المقابل ، بحيث يقطع الموصل خطوط المجال المغناطيسي. 2 . تقريب أو إبعاد مغناطيس من ملف على نحو ما هو مبين في الشكل ( ب ). ويُسمّى التيار الكهربائيّ المتولِّد في هذه الطريقة بالتيار الحثي Induced current أي أن التيار الكهربائي الحثي هو التيار الناشئ عن حركة موصل بحيث يقطع خطوط المجال الكهربايئ أو تغير التدفق المغناطيسي الذي يخترق ملف. |
الشكل: أ الشكل : ب |
|
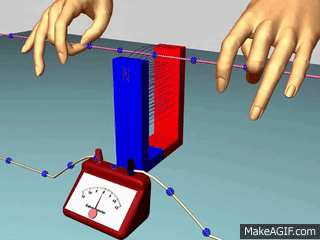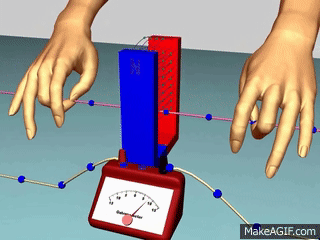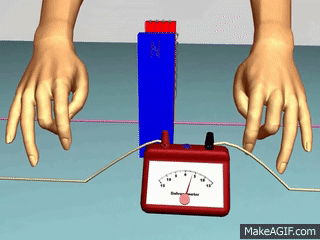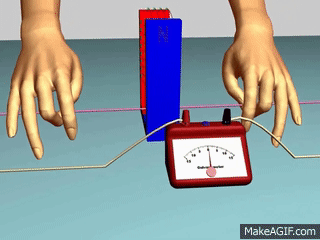
القوّة الدافعة الكهربائيّة الحثّية (` Induced electromotive force (ε يوضّح المشهد المتحرك المقابل ملفًّا موصولً بغلفانوميتر، ومغناطيس مستقيم. عند تحريك المغناطيس نحو الملف، ينحرف مؤشّر الغلفانوميتر في اتّجاه معيّن، دالًّ على تولّد قوة دافعة كهربائية حثّية وسريان تيار كهربائي حثّي في الملف، وعند إبعاد المغناطيس عن الملف، فإنّ مؤشّر الغلفانوميتر ينحرف في اتّجاه معاكس لاتّجاه انحرافه في الحالة السابقة، دالاً على تولّد قوّة دافعة كهربائيّة حثّية، وسريان تيار كهربائيّ حثّي في الملف باتجاه معاكس،كما أشاهد في كل من الشكلين ( أ ) و ( ب ).
|
|
|
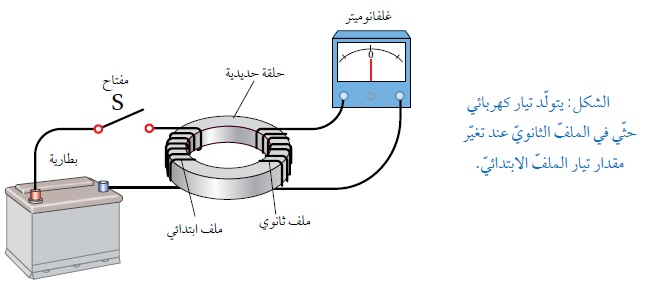
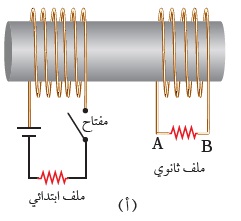
أستنتج مما سبق أن حركة المغناطيس بالنسبة للملف أو حركة الملف بالنسبة للمغاطيس يولد تيار حثي في الملف بسبب تغير التدفق المغناطيسي الناتج عن المغناطيس والذي يخترق الملف. نعلم أن مرور تيار متغير عن طريق بطارية في ملف( ملف ابتدائي) يولد حوله مجال مغنطيسي متغير،إذا اخترق ملف آخر ( ملف ثانوي) يولد في الاخير قوة دافعة كهربائية حثية وتيار حثي. كما في الشكل التالي:
مما سبق أتوصل أنه يمكن توليد قوّة دافعة كهربائيّة حثّيّة وتيّار كهربائيّ حثّي في ملفّ عند تغيّر التدفّق المغناطيسيّ( ) الذي يخترقه وبأي طريقة من الطرق التالية: 1 - مقدار المجال المغناطيسيّ. 2- المِساحة التي يخترقها المجال المغناطيسيّ. 3- الزاوية المحصورة بين متجهي المجال المغناطيسيّ والمِساحة. |
مثال 3: يوضّح الشكل التالي ملفًّا دائريًّا مغمورًا في
مجال مغناطيسيّ منتظم باتجاه محور ( -z ).
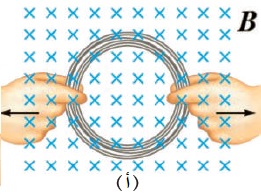
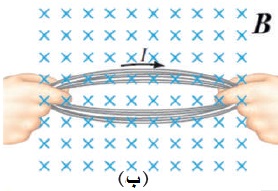
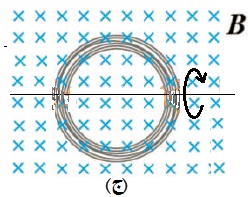
هل يتولّد تيار كهربائيّ حثّي في الملف:
أ. عند تحريك الملف نحو اليسار أو نحو اليمين مع
بقائه داخل المجال كما في الشكل أ
ب. في أثناء تغيير شكل الملف كما في الشكل ب.
ج. عند دوران الملف حول محور متعامد مع اتجاه
المجال، كما في الشكل ج.
الحل:
أ. لا يتولّد تيار كهربائيّ حثّي عند تحريك الملف داخل المجال
نحو اليسار أو اليمين بسبب ثبات التدفق المغناطيسي
ب. عند شدّ الملف يتغير شكله بحيث تقل مساحة سطحة،
فيقلّ التدفّق المغناطيسي الذي يخترقه، ما يؤدي إلى تولّد
قوة دافعة كهربائية حثّية، وتيار كهربائي حثّي.
ج. عند دوران الملف حول محور متعامد مع اتجاه المجال
المغناطيسي، تتغير الزاوية بين متجهي المجال والمساحة
بالتالي يتغير التدفق المغناطيسي الذي يخترق الملف، ما يؤدي
إلى تولّد قوة دافعة كهربائية حثّية، وتيار كهربائي حثّي
تمرين:
يوضّح الشكل التالي ملفًّا دائريًّا مغمورًا في مجال مغناطيسيّ
منتظم عموديّ على سطح الملف. أُفسّر ما يحدث في أثناء
تدويرالملف في المجال المغناطيسيّ ، على نحو ما هو موضَّح
في الشكل التالي:
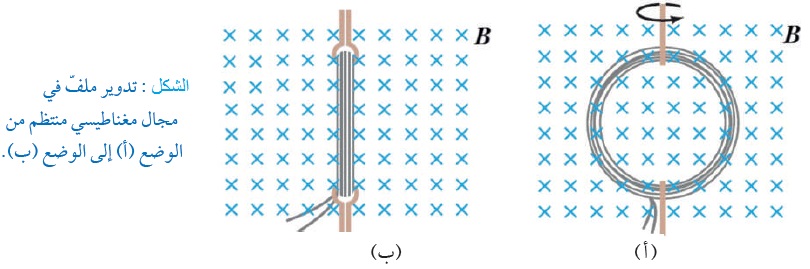 .
.
قانون فارادي في الحثّ
Faraday’s Law of Induction
توصل العالم فرادي إلى قانون يسمى قانون فرادي
الذي ينصّ قانون فارادي على أنّ:
((مقدار القوّة الدافعة الكهربائيّة الحثّيّة المتولّدة في
دارة كهربائيّة يتناسب طرديًّا مع المعدل الزمنيّ لتغيّر
التدفّق المغناطيسيّ الذي يخترقها )).
ويُعبَّر عن القوة الدافعة الكهربائية الحثية المتوسطة
رياضيًّا على النحو الآتي:
وإذا كانت الدارة مكوّنة من ( N) لفّة، فإنّ قانون فارادي
في الحثّ يُعبَّر عنه بالعلاقة الآتية:
وتقاس بوالمعنى الفيزيائيّ للإشارة السالبة سيتضّح
فيما بعد عند دراسة قانون لنز.
|
مثال 4: ملفّ دائري عدد لفّاته ( 20 ) لفة، متوسط نصف قُطر اللفّة الواحدة ( 1.0cm) موضوع في مجال مغناطيسيّ منتظم مقداره ( 120mT )، على نحو ما هو موضّح في الشكل المقابل، سُحِب الملفُّ خارج المجال المغناطيسيّ خلال زمن مقداره ( 0.2s)، أحسبُ القوّة الدافعة الكهربائيّة الحثّيّة المتوسطة المتولّدة في الملفّ. الحل: بداية، أحسب مِساحة المقطع العرضيّ للملفّ. A = π r2= π × (1.0 × 10-2)2 = 3.14 × 10-4 m أحسب القوّة الدافعة الكهربائيّة الحثّيّة المتوسطة المتولّدة في الملف على النحو الآتي، مع ملاحظة أنّ التدفّق المغناطيسيّ النهائيّ يساوي صفرًا، حيث المجال المغناطيسي الذي يخترق الملف يساوي صفر:
مثال 5: ملفّ دائريّ عدد لفّاته ( 100 ) لفة، ومِساحة مقطعه العرضي ( 1.2x10-4m2 )،موضوع في مجال مغناطيسيّ منتظم مقداره ( 1.0T )، على نحو ما هو موضّح في الشكل المجاور. بداية، مستوى الملف موازٍ لخطوط المجال المغناطيسي، ثمّ دار الملف بزاوية مقدارها ( 90˚ ) حول محور رأسيّ بحيث أصبح مستواه عموديًّا على اتّجاه المجال المغناطيسيّ خلال ( 0.50s). أحسب ما يأتي: أ . التغيّر في التدفّق المغناطيسيّ عبر مقطع الملف. ب. القوّة الدافعة الكهربائيّة الحثّيّة المتوسطة المتولدة عبر الملف. ج. التيّار الكهربائيّ الحثّي المتوسط المارّ في الملف، إذا علمت أنّ المقاومة الكهربائيّة للملف ( 4.0 Ω ). الحل: أ - أحسب التغيّر في التدفّق المغناطيسيّ عبر مقطع الملف.
ب. أحسب القوّة الدافعة الكهربائيّة الحثّيّة المتوسطة المتولدة عبر الملف.
ج. أحسب التيّار الكهربائيّ الحثّي المتوسط المارّ في الملف، إذا علمت أنّ المقاومة الكهربائيّة للملف ( 4.0 Ω ).
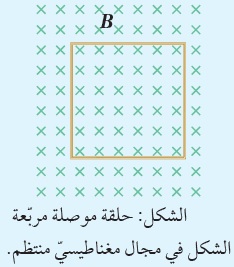
تمرين: حلقة مربّعة الشكل مقاومتها ( 10 Ω )، موضوعة في مجال مغناطيسيّ منتظم، حيث مستواها عموديٌّ على اتّجاه المجال المغناطيسيّ على نحو ما هو موضّح في الشكل المقابل. إذا تغيّر التدفّق المغناطيسي الذي يخترق الحلقة من قيمة ابتدائية (0.15Wb) ) إلى ( 0.10Wb) خلال (0.01s )، أحسب ما يأتي: أ . القوة الدافعة الكهربائية الحثّيّة المتوسطة المتولّدة في الحلقة. ب. التيار الكهربائي الحثّي المتوسط المار في الحلقة. الحل أ-
ب-
|
|
|
القوّة الدافعة الكهربائيّة الحثّية في موصِل متحرّك Motional EMF يوضح الشكل ( أ ) المجاور موصل طوله () يتحرك بسرعة ( v ) باتجاه ( +x ) داخل مجال مغناطيسي منتظم باتجاه ( +z ) بحيث يتعامد طول الموصل مع المجال المغناطيسي، حيث تتأثر الإلكترونات الحرة التي تتحرك باتجاه حركة الموصل بقوة مغناطيسيّة باتجاهمحور (+y ) حسب قاعدة اليد اليمنى. بالتالي تتجمّع شحنات سالبة عند طرف السلك(a) ، تاركةً خلفها شحنات موجبة عند الطرف ( b). فيصبح جهد الطرف ( b) الموجب أكبر من جهد الطرف( a) السالب، أيْ يتولّد فرق في الجهد الكهربائي بين طرفيه، يُسمّى: القوة الدافعة الكهربائيّة الحثّيّة ( ) وتعطى القوّة الدافعة الكهربائيّة الحثّيّة المتولّدة في هذا الموصل بالعلاقة الآتية:
وعندما يكون الموصل جزء من دارة كهربائية مغلقة تحوي مقاومة ( R )،فسيري تيار حثي باستمرار حركة الموصل، كما في الشكل المجاور (ب ) ويحسب التيار الحثي حسب قانون أوم:
مما سبق أتوصل أن القوة الدافعة الكهربائية الحثية المتولدة في موصل يتحرك بحيث طوله متعامد مع مجال مغناطيسي منتظم يعتمد على العوامل التالية: - مقدار المجال المغنطيسي. - طول الموصل. - سرعة الموصل.
|
|
مثال 6:
يتقابل القطبان الشماليّ N والجنوبيّ S لمغناطيسين،
طول كلٍّ منهما ( ℓ = 20.0 cm )، وارتفاعه (h = 6.00 cm)
بينهما مجال منتظم مقداره (54mT). أتأمّل الشكل التالي:
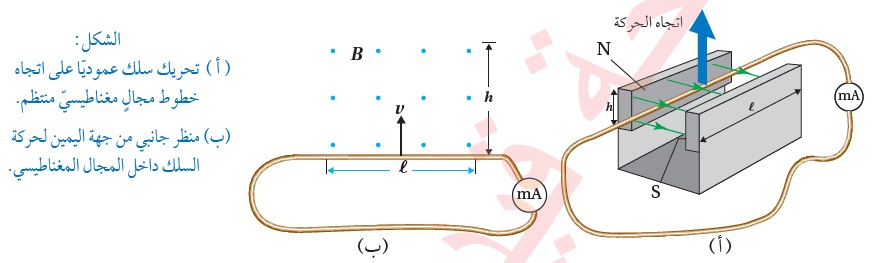
حُرِّك سلكٌ مشدودٌ موصولٌ بملي أميتر من الطرف السفلي
للمغناطيسين إلى الطرفالعلويّ عموديًّا على اتّجاه خطوط
المجال المغناطيسيّ خلال مدّة زمنيّة مقدارها (0.2s)،على نحو
ما هو موضح في الشكل . أحسب ما يأتي:
أ . القوة الدافعة الكهربائيّة الحثّيّة المتولّدة في السلك.
ب. التيّار الكهربائيّ الحثّي المارّ في الملي أميتر إذا علمت أنّ
المقاومة الكهربائيّة للدارة ( 2.0 Ω ).
الحل:
أ. طول السلك داخل المجال المغناطيسيّ يساوي طول
أيٍّ من المغناطيسين. أحسب القوّة الدافعة الكهربائيّة
الحثّيّة المتولّدة فيه على النحو الآتي ، حيث أحتاج إلى إيجاد
سرعة السلك المشدود كما يلي:
ب. أحسب التيار الكهربائيّ الحثّي المارّ في الدارة على
النحو الآتي:
مثال 7:
سيارة تتحرك أفقياً بسرعة ثابتة ( ) باتجاه الشمال
الجغرافي، لها واقي صدمة ( دعامه ) طوله ( 1.5m )،
ونشأت قوة دافعة كهربائية حثية في الدعامة مقدارها
(3mV )، إذا علمت أن المركبة الرأسية للمجال المغناطيسي
الأرضي في منطقة حركة السيارة تساوي ( ).
أحسب مقدار السرعة التي تتحرك بها السرعة.
الحل:
مثال 8:
يمثل الشكل التالي موصل ( a,b )، طوله ( 1m)،
ينزلق على سلكين نحاسيين متوازيين ومتصلين
مع مقاومة ( ); كما في الشكل.
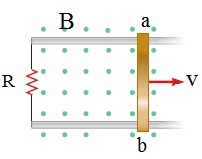
ما مقدار القوة اللازم تطبيقها على الموصل لتحريكه
بسرعة ثابتة ( 1.5m/s ) نحواليمين؟
الحل:
مقدار القوة المغناطيسية = القوة الخارجية المطبقة
لأن الموصل يتحرك بسرعة ثابتة.
|
قانون لنز Lenz’s Law لاحظت في طرائق توليد القوة الدافعة الكهربائيّة الحثّية والتيار الكهربائي الحثّي السابقة أنّ مؤشّر الغلفانوميتر أو الأميتر ينحرف باتّجاه معيّن عند تقريب أحد قطبي مغناطيس من ملف، وأن اتّجاه الانحراف ينعكس عند إبعاد القطب نفسه عن الملف. فما دلالة هذه المشاهدات؟ وكيف أُحدّد اتجاه التيار الكهربائي الحثّي المتولّد؟
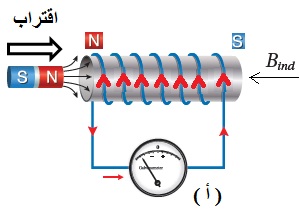
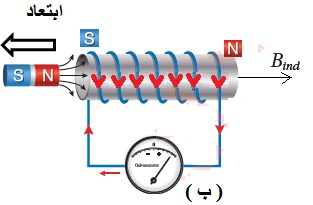
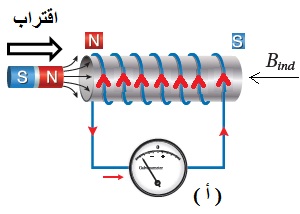
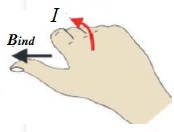
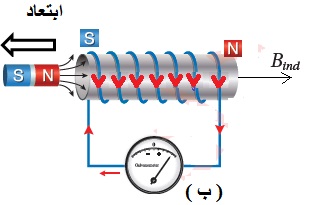
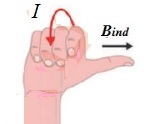
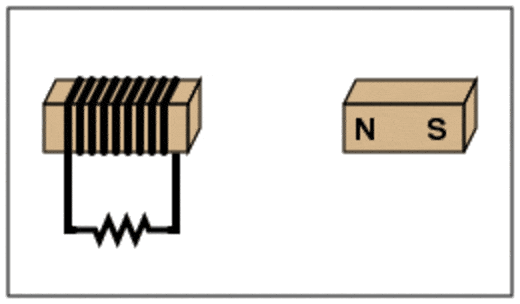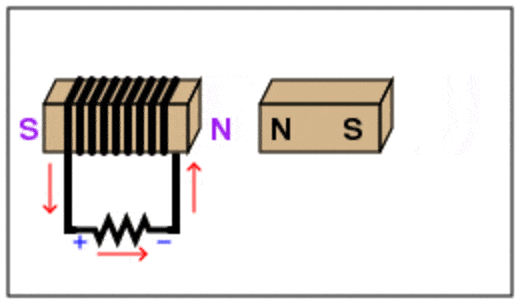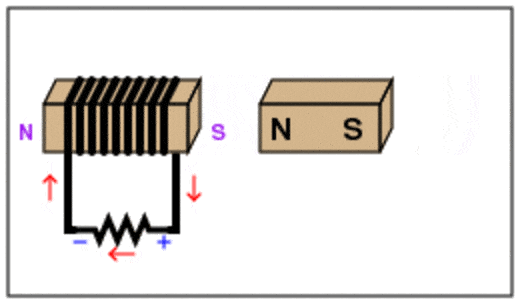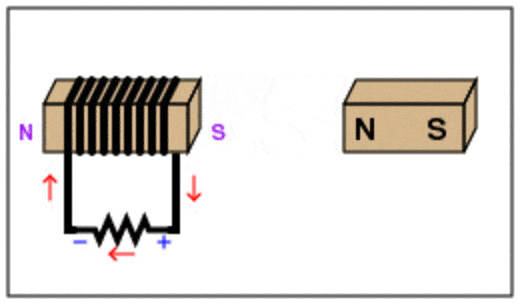
ينصّ قانون لنز على أنّ: ((يكون اتجاه التيار الحثي المتولد في دارة مغلقة بحيث يولد مجالً مغناطيسيًا يقاوم التغير في التدفق المغناطيسي المسبب له )) . وهذا يُفسّر وجود الإشارة السالبة في قانون فارادي. وتشير إلى أن إشارتي القوة الدافعة الكهربائيّة الحثّية والتغيّر في التدفّق المغناطيسي متعاكستان.أي أنه إذا كان التدفق المغناطيسي متزايد ، تكون القوة الدافعة الكهربائية الحثية سالبة، وإذا كان التدفق متناقص تكون القوة الدافعة الكهربائية الحثية موجبة. لتحديد اتجاه التيار الكهربائي الحثّي المتولّد اعتمادا على قانون لنز أتبع الخطوات التالية بالترتيب: أولا- أعين اتجاه المجال المغناطيسي والمؤثر على الملف. ثانياً - أحدد كون المجال المغناطيسي المؤثر متزايد أو متناقص. ثالثاً - إذا كان التدفق متزايد ، ينشأ في الملف تيار حثي يولد مجال مغناطيسي حثي ( ) بعكس اتجاه المجال المغنطيسي المؤثر، لمقاومة الزيادة في التدفق المغناطيسي. كما ألاحظ في الشكل ( أ ) المقابل. - إذا كان التدفق متناقص ، ينشأ في الملف تيار حثي يولد مجال مغناطيسي حثي باتجاه المجال المغناطيسي المؤثر لمقاومة النقص في التدفق المغناطيسي كما ألاحظ في الشكل( ب ) المجاور. - أستخدم قاعة اليد اليمنى لتحديد اتجاه التيار الحيثي بالاعتماد على اتجاه المجال المغناطيسي الحثي. حيث يُشير الإبهام إلى اتّجاه المجال المغناطيسي الحثي الناتج عن الملف ( Bind )، في حين يُشير اتجاه انحناء بقيّة الأصابع إلى اتّجاه التيار الكهربائي الحثّي في لفّات الملف. كما في الشكل المقابل.
ألاحظ عند تقريب قطب مغناطيسي شمالي يتكون على الطرف القريب للملف قطب مشابه أي قطب شمالي كما في الشكل( أ )، وعند إبعاد القطب مغناطيسي شمالي يتكون على الطرف القريب للملف قطب مخالف أي قطب جنوبي كما في الشكل( ب )،
|
|
|
مثال 9: يقترب القطب الشمالي لمغناطيس من ملف، فيتحرك مؤشّر المليميتر المتصل به. ويوضّح الشكل (أ) منظرًا جانبيًّا للمغناطيس في أثناء اقترابه من الملف. كيف أُحدّد اتّجاه التيار الكهربائي الحثّي المتولّد في الملف وما اتجاهه عند النظر إلى الملف من الأعلى؟ الحل: بحسب قانون لنز، يكون اتّجاه التيار الكهربائي الحثّي المتولّد في الملف الاتجاه الذي ينشأ عنه مجالمغناطيس حثي يُقاوم التغيّر في التدفّق المغناطيسي المسبّبَ في توليده. وفي هذا الشكل، يكون اتّجاه التيار الحثّي في الملف، بحيث يولّد مجالاً مغناطيسيًّا داخل الملف نحو الأعلى؛ وباستخدام قاعدة اليد اليمنى أستنتج أنّ اتجاه التيار الكهربائي الحثّي المتولّد في الملف يكون بعكس اتجاه حركة عقارب الساعة عند النظر إليه من الأعلى أيْ يكون الطرف العلويّ للملف قطبًا مغناطيسيًّا شماليًّا؛ كي يقاوم اقتراب القطب الشمالي للمغناطيس المؤدّي توليده. كما ألاحظ في الشكل ب والمشهد المتحرك المقابل. |
( أ ) منظر جانبي لتقريب القطب الشمالي لمغناطيس من أحد طرفي ملف. المتولّد في الملف واتجاه المجال التيار. |
|
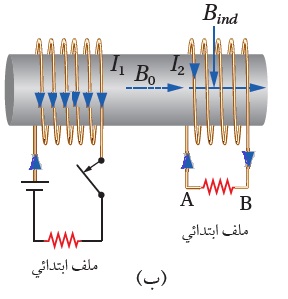
مثال10: لُفّ ملفّان عدد لفات كلٍّ منهما ( 100 ) لفة، ومساحة المقطع العرضي لكلّ منهما 3x10-4m2، على قلب حديدي على نحو ما هوموضّح في الشكل (أ). عند إغلاق مفتاح دارة الملف الابتدائيّ يتولّد مجال مغناطيسي داخله مقدارُه ( B0 = 180 mT ) ينتقل عبر القلب الحديدي، على نحو ما هو موضّح في الشكل (ب)، وعند فتح الدارة الكهربائيّة يتلاشى هذا المجال المغناطيسيّ خلال ( 0.10 s ). أُجيبعمّا يأتي: أ . أحسب القوة الدافعة الكهربائيّة الحثّية المتوسطة المتولّدة في الملف الثانويّ لحظة فتح المفتاح .S ب. أُحدّد اتجاه سريان التيار الكهربائيّ الحثّي في المقاومة الكهربائيّة في الملف الثانويّ لحظة فتح المفتاح. الحل: أ- التغيّر في التدفّق المغناطيسي ناتج عن تغيّر مقدار المجال المغناطيسي الذي يخترق حلقات الملف الثانوي، وأحسب القوة الدافعة الكهربائيّة الحثّية المتوسطة المتولّدة في الملف على النحو الآتي:
ب- المجال المغناطيسي الناتج عن الملف الابتدائي يكون نحو اليمين وينتقل عبر القلب الحديدي، وعند فتحدارة الملف الابتدائي، يقلّ التدفّق المغناطيسي الذي يخترق الملفّ الثانوي، فتتولّد قوة دافعة كهربائية حثّية بين طرفيه تؤدّي إلى مرور تيار كهربائي حثّي في الملف في الاتجاه الذي تجعله يُقاوم النقص في التدفّق المغناطيسي؛أيْ يكون المجال المغناطيسيّ الحثّي باتجاه المجال المغناطيسيّ نفسه. وبتطبيق قاعدة اليد اليمنى نجد أن اتّجاه التيار الكهربائيّ الحثّي المارّ في المقاومة يكون من B إلى A، كما ألاحظ في الشكل (ب ) المقابل. |
|
|
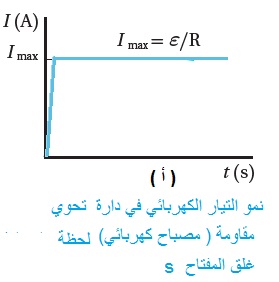
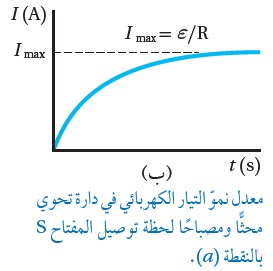
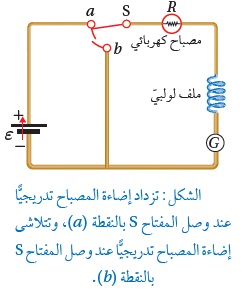
الحثّ الذاتيّ Self Induction ألاحظ في الشكل ( أ ) المجاور أن المصباح( مقاومة) يضيء بسرعة، أي أن التيار يصل إإلى قيمته العظمي بكل لحظي تقريباًعند غلق المفتاح، كما ألاحظ في الرسم البياني أسفل الشكل(أ ).كما أن المصباح ينطفئ لحظياً عند فتح المفتاح. الشكل (ب ) يوضح دارة كهربائيّة تحوي بطارية ومقاومة (مصباح) وملفًّا لولبيًّا ومفتاح ( S). عند إغلاق المفتاح ( s ) تزداد شدة إضاءة المصباح تدريجيًّا حتى تثبت، ما يعني أنّ التيار لا يصل إلى قيمته العظمى لحظيًّا، بل ينمو تدريجيًّا من الصفر إلى قيمته العظمى، على نحو ما هو مبين في الرسم البياني أسفل الشكل (ب)، كما أن المصباح ينطفئ تدريجياٍ عند فتح المفتاح.
|
شكل: أ شكل: ب |
|
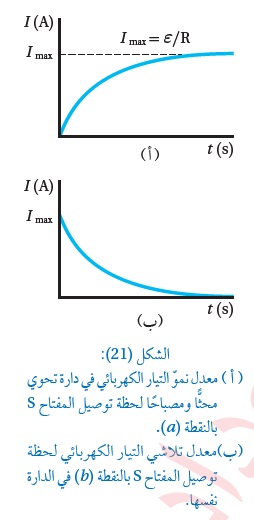
التفسير: وجود الملفّ اللولبيّ أعاق نموّ التيار الكهربائيّ الناتجعن البطارية. فعند وصل المفتاح ( S) مع النقطة ( a )يسري التيار الكهربائيّ في الدارة الكهربائيّة، فيتولّد مجال مغناطيسيّ في الملف اللولبيّ، ويزداد التدفّق المغناطيسي الذي يخترقه. وبحسب قانون لنز، ينشأ فيه قوة دافعة كهربائيّة حثّية ذاتيّة تعاكس القوة الدافعة الكهربائيّة (ε) للبطارية، ما يؤدّي إلى نموّ التيار الكهربائي إلى قيمته العظمى تدريجيًّا وليس لحظيًّا. كما في الرسم البياني المجاور ( أ ). ويوضّح الرسم البياني ( ب ) أنّ التيّار الكهربائيّ يتلاشى تدريجيًّا لحظةفتح المفتاح ( S) بالنقطة ( b) في الدارة الكهربائيّة الموضّحة في حيث لا يصل مقداره إلى الصفر لحظياَ، بل يتلاشى تدريجياً لأن التدفق المغنطيسي في الملف يتناقص وتنشأ فيه قوة دافعة كهربائيّة حثّية ذاتيّة بنفس اتجاه القوة الدافعة الكهربائيّة (ε) للبطارية لمقاومة التناقصفي التدفق المغناطيسي. ويسمى الملف اللولبي محثًّا Inductor، ويرمز له في الدارة الكهربائية بالرمز التالي: ملاحظة مهمة: عندما يصل التيار في المحث إلى قيمته العظمى( ثبات التيار) ينعدم الحث، وعندها يكون الملف كمقاومة فقط ولا يعامل كمحث. مما سبق، يُعرف الحث الذاتي بأنّه تولّد قوة دافعة كهربائيّة حثّية ذاتيّة في دارة كهربائيّة مغلقة تحوي ملف لولبي نتيجة تغيّر التدفّق المغناطيسيّ بسبب تغيّر مقدار تيار الدارة نفسها. |
|
التغير في التدفق المغناطيسي ناتج عن تغير التيار الكهربائي،
والقوة الدافعة الكهربائيّة الحثّية الذاتيّة ( ε`L ) تتناسب طرديًّا
مع المعدل الزمني للتغيّر في مقدار التيار الكهربائيّ ( )،
وأُعبّر عن ذلك رياضيًّا بالعلاقة التالية:
حيث ( ) ثابت التناسب، ويُسمّى معامل الحثّ الذاتيّ للمحثّ
أو محاثّة المحثّ: وتُعَرف على أنها نسبة القوة الدافعة الكهربائيّة
الحثّية الذاتيّة المتولّدة بين طرفي محثّ إلى المعدل الزمني للتغيّر
في مقدار التيار الكهربائيّ المارّ فيه.
وهو أيضاً مقياس لممانعة المحثّ للتغيّر في مقدار التيار الكهربائيّ
المارّ فيه، ووحدة قياسه هي ( V.s/A )، وتُسمّى هنري ( H ).
تعريف الهنري ( H ):
محاثّة محثّ تتولّد بين طرفيه قوة دافعة كهربائيّة حثّية ذاتيّة
مقدارها ( 1 V )، عندما يكون المعدّل الزمني للتغيّر في مقدار
التيار الكهربائيّ المارّ فيه ( 1 A ).
مثال 11:
ملف لولبي يتكون من 100 لفة، تغير التيار المار فيه
من 4A إلى 6A خلال فترة زمنية 0.01s، وتولد في الملف
قوة دافعة كهربائية حثيىة ذاتية مقدارها 0.4V.
أحسب ما يأتي:
أ. محاثة الملف.
ب. التغير في التدفق المغناطيسي في الملف.
الحل:
أ. أجد محاثة المحث:ت بما أن التيار الكهربائي متزايد يولد
تدفقاً مغناطيسي متزايد ، لذلك تكون القوة الدافعة
الكهربائية الحثية الذاتية سالبة وذلك حسب قانون لنز.
ب. أجد مقدار الزيادة في التدفق المغناطيسي
باستخدام قانون فراداي:
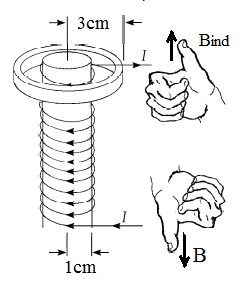
مثال 12:
حلقة فلزية نصف قطرها ( 3cm ) ومقاومتها ( )،
وضعت عند أحد طرفي ملف لولبي عدد لفاته 1000 لفة
لكل متر ، ونصف قطره 1cm، كما في الشكل التالي:
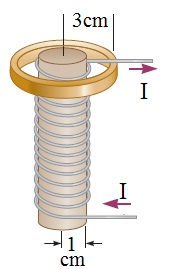
إذا كان المجال المغناطيسي الناشئ عن الملف اللولبي
يساوي نصف المجال المغناطيسي عند مركزه، وتغير
التيار فيه بمعدل 200A/s، ما مقدار واتجاه المجال
المغناطيسي الناشئ عن التيار الحثي المتولد في الحلقة؟
الحل:
مساحة المقطع العرضي للملف:
عدد اللفات لوحدة الطول من الملف اللولبي:
لفة/ متر
ومعدل تغير التيار:
والمجال المغناطيسي المؤثر على الحلقة يساوي
نصف المجال عند مركز الملف والمؤثر على الحلق:
أستخدم قانون فرادي لأيجاد القوة الدافعة الكهربائية
الحثية في الحلقة الناتجة عن تغيرالتيار:
ومن ذلك التيار الحثي:
المجال المغناطيسي الحثي في الحلقة:
|
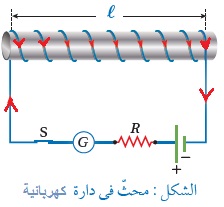
على ماذا تعتمد محاثة الملف اللولبي؟ إذا كان هناك محثًّا طوله ( ℓ)، ومساحة مقطعه العرضي (A)،وعدد لفّاته ( N) في دارة كهربائيّة ; كما في الشكل المجاور.لحظة غلق المفتاح يتزايد كل من مقدار التيار الكهربائيّ المارّ في الدارة تدريجيًّا من ومقدار التدفّق المغناطيسيّ الذي يخترق المحثّ من قيمة الصفر لكل منهما خلال المدّة الزمنيّة نفسها. فيتولّد بين طرفي المحثّ قوة دافعة كهربائيّة حثّية ذاتيّة. وبحسب قانون فارادي في الحثّ، يُعبَّر عن مقدارها المتوسط بالعلاقة الآتية:
وأتذكر أن المجال المغناطيسي الناشئ عن مرور تيار في ملف لولبي يساوي:
بتعويض المعادلة ( 2 ) في المعادلة ( 1)، أحصل على:
من هذه العلاقة،أستنتج أن محاثة الملف اللولبي، لا تعتمد على مقدار التيار المار فيه، بل تعتمد على: - النفاذية المغناطيسية( ) للمادة الملفوف عليها الملف ( قلب الملف) - عدد لفات الملف والعلاقة طردية بين المحاثة ومربع عدد لفات الملف( N ). - مساحة المقطع العرضي للملف( A ) والعلاقة بين المحاثة والمساحة طردية - طول الملف ( )، والعلاقة عكسية بين المحاثة وطول الملف. |
 |
مثال 13 :
إذا علمت أنّ طول محثّ يساوي ( 20cm )، ومساحة
مقطعه العرضي ( 2.5x10-5m2)،وعدد لفّاته ( 200 ) لفة،
والمحثّ ملفوف حول أنبوب كرتونيّ يملؤه الهواءُ، ويسري
فيه تيارٌ كهربائيّ ( 5A )،
أحسب ما يأتي:
أ . معامل الحثّ الذاتيّ للمحثّ.
ب. التدفّق المغناطيسيّ الذي يخترق المحثّ.
ج. القوة الدافعة الكهربائيّة الحثّية الذاتيّة المتوسطة
المتولّدة في المحثّ إذا عكست اتجاه التيار الكهربائي
المارّ فيه خلال ( 0.1s).
الحل:
أ . أستخدم العلاقة الآتية لحساب معامل الحثّ الذاتيّ
للمحثّ مع استخدام النفاذيّة المغناطيسيّة للهواء:
ب. أحسب التدفّق المغناطيسيّ باستخدام العلاقة الآتية:
ج. أستخدم العلاقة الآتية لحساب القوة الدافعة الكهربائيّة
الحثّية الذاتيّة المتوسطة المتولّدة في المحثّ:
|
المحوّل الكهربائي ونقل الطاقة يستخدم المحول الكهربائي كهربائي في حياتنا اليومية، لشحن الهاتف ومصابيح الطوارئ وغيره.نقل الطاقة الكهربائيّة إلى مسافات كبيرة تؤدّي المقاومة الكهربائية للأسلاك الناقلة إلى ضياع كبير في الطاقة الكهربائية حسب العلاقة ( P=RI2 ). وللتقليل من هذه الطاقة يتم تقليل التيار ورفع الجهد ثم خفض هذا الجهد للاستخدام المنزلي عن طريق المحول الكهربائي الذي يعمل على مبدأ الحث الكهرومغناطيسي. |
محول شاحن الهاتف
محولات كهربائية لنقل الطاقة الكهربائية |
|
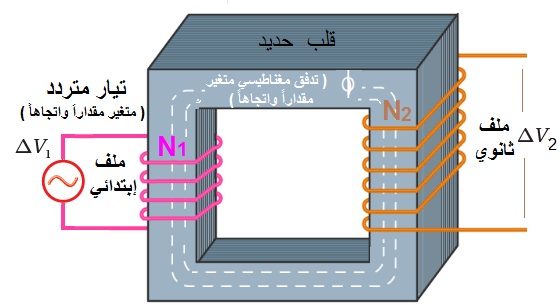
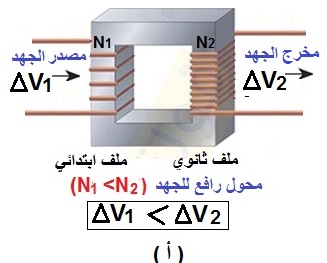
مكونات المحول الكهربائي: 1- الملف الابتدائي:ويتكوّن من ( N1 ) لفة، ويتصل بمصدر فرق جهد متغير مقدارًا واتجاهًا، يُسمّى مصدر فرق الجهد المتردّد ( ). 2- الملف الثانوي:يتكوّن هذا الملف من ( N2 ) لفة، ويتصّل بجهاز مستهلك للطاقة، مثل مقاومة أو مصباح تعمل على فرق جهد ( ). 3- القلب الحديدي:يعمل القلب الحديدي على زيادة المجال المغناطيسي داخل الملف الابتدائي،و الحصول على تدفّقِ أكبر من خطوط المجال المغناطيسي الواصلة إلى الملف الثانوي، |
الشكل : مكونات محول كهربائي |
- يتولد في الملف لابتدائي تدفقاً مغناطيسياً متغيراً
لأن() مصدر الجهد المتردد يولد تيار متردد، فيتولد
في الملف الابتدائي قوة دافعة كهربائية حثية مترددة،
حسب قانون فراداي:
ويقوم القلب الحديدي للمحول بتركيز التدفق المغنطيسي
المتولد في الملف الابتدائي على الملف الثانوي، فيتولد فيه
قوة دافعة كهربائية حثية، حسب قانون فرادي:
وبقسمة المعادلة ( 1 ) على المعادلة (2 )، نحصل على
الصيغة التالية:
|
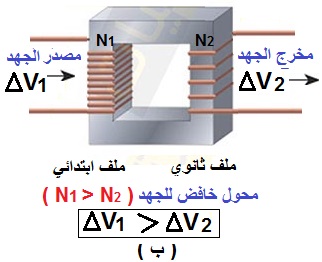
المحولات نوعان: محول كهربائي رافع للجهد: - فرق الجهد الخارج من المحول أكبر من فرق جهد المصدر،أي أن:
- عدد لفات الملف الثانوي أكبر من عدد لفات الملف الابتدائي، أي أن: كما في الشكل ( أ ) المقابل. محول كهربائي خافض للجهد: - فرق الجهد الخارج من المحول أقل من فرق جهد المصدر،أي أن: . - عدد لفات الملف الثانوي أقل من عدد لفات الملف الابتدائي، أي أن: كما الشكل ( ب) المجاور. - وفي المحوّل المثالي تكون القدرة الداخلة في الملف الابتدائي مساوية للقدرة الناتجة عن الملف الثانوي، حسب العلاقة:
- والمحوّلات المستخدمة عمليًّا لا تكون مثالية، إذ أن القدرة التي نحصل عليها من الملف الثانوي تكون أقلّ من القدرة التي يُزوّد بها الملف الابتدائي للمحوّل، بسبب استهلاك قدرة في مقاومة أسلاك نقل الطاقة الكهربائية، لمسافات طويلة:
- لخفض القدرة الضائعة، يُستخدم محوّل رافع للجهد فيمحطات توليد الطاقة لرفع الجهد إلى نحوِ 230 kV) )؛ ما يؤدّي إلى خفض قيمة التيار الكهربائي في خطوط نقل الطاقة،ثمّ تُستخدم محوّلات خافضة للجهد حتى تصل قيمة فرق الجهد في الأحياء السكنية إلى ( 230 V ). |
|
مثال 14:
محوّل كهربائي مثالي خافض للجهد يتصل ملفّه الابتدائي
بمصدر فرق جهد ( 240V )، ويتصل ملفّه الثانوي بمصباح
كهربائي مقاومته ( 2 Ω )، وعدد لفّات الملف الابتدائي ( 1200 ) لفة،
ولفّات الملف الثانوي ( 30 ) لفة.
أ . أحسب فرق الجهد بين طرفي الملف الثانوي.
ب. أحسب التيار في الملف الابتدائي
الحل:
أ. فرق الجهد بين طرفي الملف الثانوي.
ب. التيار الكهربائيّ المار في الملف الابتدائي.
بما أن المحول الكهربائي مثالي، لذلك:
مثال 15:
ملف كهربائي مثالي يعمل على مصدر جهد 240v، ونسبة
عدد لفات الملف الابتدائئ إلى عدد لفات الملف الثانوي
تساوي 20، والقدرة الناتجة في الملف الثانوي 48W.
بناءأ على ذلك أجب عما يلي:
1- هل المحول رافع أم خافض للجهد؟ فسر إجابتك.
2- ما مقدرا قدرة الملف الابتدائي.
3- أحسب فرق جهد الملف الثانوي.
4 - احسب التيار المار في الملف الابتدائي.
الجواب:
أ- المحول خافض للجهد، لأن عدد لفات الملف الثانوي
أقل من عدد لفات الملف الابتدائي.
من المعطيات:
ب- بما أن المحول مثالي ، لذلك قدرة الملف الابتدائى
تساوي قدرة الملف الثانوي:
ج- فرق جهد الملف الثانوي:
ج- التيار المار في الملف الابتدائي:
المحول مثالي:
التيار المار في الملف الثانوي: