التكامل بالتعويض

الدرس السادس: التكامل بالتعويض

 

سنتعرف في هذا الدرس إلى:

استخدام طريقة جديدة لإجراء التكامل وتسمى التكامل بالتعويض؛ حيث سنستخدمها في إيجاد:

1. التكاملات غير المحدودة

2. التكاملات  المحدودة

 

أولًا: التكامل بالتعويض للتكاملات غير المحدودة:

تعلمنا إيجاد الاقتران الأصلي باستخدام التكامل بناء على قواعد الاشتقاق ؛

ولكن أحيانًا لا تنجح الطرائق السابقة لإيجاد الاقتران الأصلي لاقترانات معينة مثل: ضرب اقترانين أو قسمتهما.

لذا؛ نحتاج إلى طرائق أخرى يمكن استخدامها، ومنها: التكامل بالتعويض.

 

التكامل بالتعويض: وهي طريقة تتضمن استعمال متغير جديد بدلًا من متغير التكامل،

                              ونستخدمه لإيجاد التكاملات التي تكون على الصورة:

                                              $\int f\left(g\right(x\left)\right) g\mathit{َ}\mathbf{ }\left(x\right) dx=\int f\left(u\right) du$ 

---

خطوات التكامل بالتعويض:

يمكن استخدام المثال الآتي لتوضيح خطوات التكامل بالتعويض:

مثال(1): أجد التكامل الآتي :

                $f\left(x\right) = \int 4x^3 {\left(5+x^4\right)}^7 dx$

الحل:

ألاحظ أنّ:

1) الاقتران المكامَل عبارة عن حاصل ضرب اقترانين.

2) ليس من السهل تحويل الاقتران إلى حاصل جمع اقترانين.

3) المقدار $\left(4 x^3\right)$ هو مشتقة ما داخل القوس  $\left(5+x^4\right)$

 

وبالتالي يمكن استخدام طريقة التعويض لإيجاد التكامل وذلك باتباع الخطوات الآتية:

الخطوة الأولى : أفترض أنّ $u$ تساوي المقدار المرفوع إلى الأس 7 ؛ أي إنّ: $u=5+x^4$ 

الخطوة الثانية : أجد مشتقة $u$ ، وهي: $\frac{du}{dx}=4 x^3$

الخطوة الثالثة : أكتب المعادلة السابقة لـتكون $dx$ في طرف مستعملًا الضرب التبادلي فتصبح: $dx=\frac{du}{4x^3}$

الخطوة الرابعة : أعيد كتابة التكامل مستعملًا المتغير $u$ بدلًا من المتغير $x$ 

                             لينتج تكاملًا جديدًا كله بدلالة المتغير الجديد $u$.

بتعويض $u=5+x^4 , dx=\frac{du}{4x^3}$                  $\int 4x^3 {(5+x^4)}^7 dx =\int 4x^3 {\left(u\right)}^7 \frac{du}{4x^3}$

بالتبسيط                                                                          $=\int u^7 du$

تكامل اقتران القوة                                                         $=\frac{1}{8} u^8 +C$

بتعويض $u=5+x^4$                                           $=\frac{1}{8} {(5+x^4)}^8 +C$

 

التحقق من صحة الحل :يمكن استخدام  قاعدة السلسلة لإيجاد مشتقة الاقتران الأصلي ومقارنة الناتج بالاقتران المُكامَل.

                                         $$\begin{gathered} \frac{d}{dx}\left(\frac{1}{8} {(5+x^4)}^8 +C\right)=\frac{1}{8}\times 8\times {\left(5+x^4\right)}^7 \left(4x^3\right) \\ = 4x^3 {\left(5+x^4\right)}^7 \end{gathered}$$        

 

ويمكن تلخيص خطوات حل التكامل بالتعويض بالمخطط الآتي: 

        

---

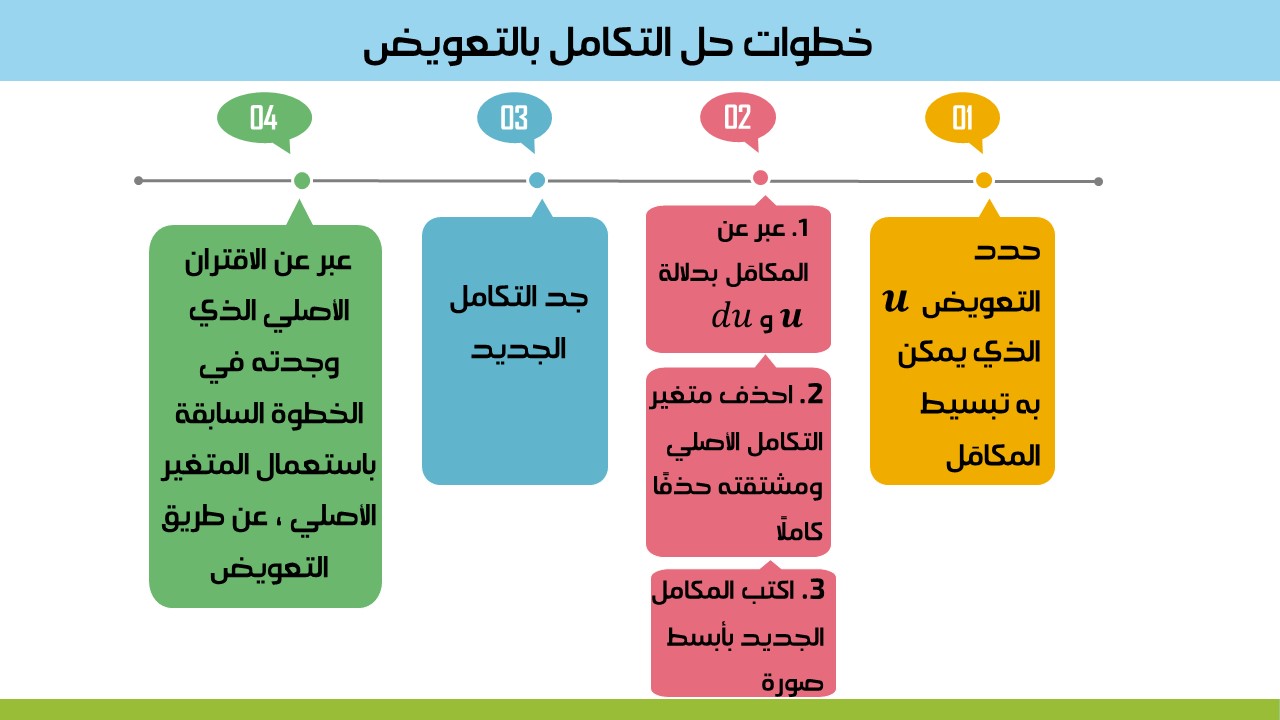
مثال(2): أجد كلًا من التكاملات الآتية :

                  $$\begin{gathered} 1) \int 4x^3\sqrt{{\left(x^4+10\right)}^5} dx \\ 2) \int x^2 e^{x^3} dx \\ 3) \int 5 {\sin }^{4}x \cos x dx \\ 4) \int \frac{{\left(\ln x\right)}^3}{x} dx \end{gathered}$$

الحل:

$1) \int 4x^3\sqrt{{(x^4+10)}^5} dx$
$4x^3=\frac{du}{dx}\Rightarrow dx=\frac{du}{4x^3}$	افترض أنّ: $x^4+10=u$
$\int 4x^3\sqrt{{(x^4+10)}^5} dx=\int 4x^3 \times \sqrt{u^5} \times \frac{du}{4x^3}$	بتعويض $$\begin{gathered} u=x^4+10 \\ dx=\frac{du}{4x^3} \end{gathered}$$
$$\begin{gathered} =\int \sqrt{u^5} du \\ =\int u^{\frac{5}{2}} du \end{gathered}$$	بالتبسيط الصورة الأسية
$=\frac{2}{7} u^{\frac{7}{2}} +C$	تكامل اقتران القوة
$$\begin{gathered} =\frac{2}{7}{\left(x^4+10\right)}^{\frac{7}{2}}+C \\ =\frac{2}{7}\sqrt{{\left(x^4+10\right)}^7 } +C \end{gathered}$$	بتعويض$u=x^4+10$ الصورة الجذرية

 

 

 

 

 

 

 

 

$2) \int x^2 e^{x^3} dx$
$3x^2=\frac{du}{dx}\Rightarrow dx=\frac{du}{3x^2}$	افترض أنّ:$x^3=u$
$\int x^2 e^{x^3} dx=\int x^2 \times e^u \times \frac{du}{3x^2}$	بتعويض $$\begin{gathered} x^3=u \\ dx=\frac{du}{3x^2} \end{gathered}$$
$=\frac{1}{3}\int e^u du$	بالتبسيط
$=\frac{1}{3}{e}^u +C$	تكامل الاقتران الأسي الطبيعي
$=\frac{1}{3} e^{x^3} +C$	بتعويض $u=x^3$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

$3) \int 5 {\sin }^{4}x \cos x dx$
$\cos x=\frac{du}{dx}\Rightarrow dx=\frac{du}{\cos x}$	افترض أنّ:$\sin x=u$
$\int 5 {\sin }^{4}x \cos x dx=5\int u^4 \times cos x \times \frac{du }{cos x}$	بتعويض$$\begin{gathered} \sin x=u \\ dx=\frac{du}{\cos x} \end{gathered}$$
$=5\int u^4 du$	بالتبسيط
$$\begin{gathered} =5\left(\frac{u^5}{5}\right) + C \\ =u^{5 }+C \end{gathered}$$	تكامل اقتران القوة
$={\sin }^{5}x +C$	بتعويض$u=sin x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

$4) \int \frac{{\left(\ln x\right)}^3}{x} dx$
$\frac{1}{x}=\frac{du}{dx}\Rightarrow dx=x du$	افترض أنّ:$ln x=u$
$\int \frac{{\left(\ln x\right)}^3}{x} dx=\int \frac{u^3}{x}\times x\times du$	بتعويض $$\begin{gathered} \ln x=u \\ dx=x du \end{gathered}$$
$=\int u^3 du$	بالتبسيط
$=\frac{u^4}{4}+C$	تكامل اقتران القوة
$=\frac{1}{4}{\left(\ln x\right)}^4 + C$	بتعويض $u=ln x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

ثانيًا: التكامل بالتعويض للتكاملات المحدودة:

طريقة التكامل بالتعويض للتكاملات المحدودة :

يوجد طريقتان لإيجاد قيمة التكامل المحدود بالتعويض، وهما:

1) إيجاد التكامل أولًا، ثم تعويض حدود التكامل الأصلية (الحدود قبل خطوة التعويض).

2) تغيير حدود التكامل عند تغيير متغير التكامل (هذه الطريقة الأكثر تفضيلًا).

 

مثال(3): أجد كلًا من التكاملات الآتية :

                       $$\begin{gathered} 1) {\int }_0^1{x}^3{\left(1+x^4\right)}^3 dx \\ 2) {\int }_{-1}^0\frac{x^3}{\sqrt{x^4+9}} dx \\ 3) {\int }_0^1 x e^{4x^2+3} dx \end{gathered}$$   

الحل:

                                                  $1) {\int }_0^1{x}^3{(1+x^4)}^3 dx$

أولًا: أفترض أنّ $u=1+x^4$ ، ومن ثم فإن:

 $\frac{du}{dx}=4x^3 \Rightarrow dx=\frac{du}{4x^3}$

ثانيًا: أغير حدود التكامل:

الحد السفلي	الحد العلوي
$$\begin{gathered} x= 0 , u = 1+ x^4 \\ u= 1 + {\left(0\right)}^4 \\ u=1 \end{gathered}$$	$$\begin{gathered} x= 1 , u = 1+ x^4 \\ u= 1 + {\left(1\right)}^4 \\ u=2 \end{gathered}$$

 

 

 

 

 

 

ثالثًا: أستخدم طريقة التكامل بالتعويض لإيجاد الناتج:

بتعويض $u=1+x^4$ ، $dx=\frac{du}{4x^3}$                             ${\int }_0^1{x}^3{(1+x^4)}^3 dx={\int }_1^2{x}^3 \left(u^3\right) \frac{du}{4x^3}$

بالتبسيط                                                                                   $=\frac{1}{4}{\int }_1^2 u^3 du$

تكامل اقتران القوة المضروب بثابت                                                $=\frac{1}{16}{u}^4 \overline{)\begin{array}{c}2\\ 1\end{array}}$

بالتعويض                                                                                   $=\frac{1}{16}\left(2^4-1^4\right)$

بالتبسيط                                                                        $=\frac{1}{16}\left(16-1\right) =\frac{15}{16}$

---

             $2) {\int }_{-1}^0\frac{x^3}{\sqrt{x^4+9}} dx$

أولًا: أفترض أنّ $u=x^4+9$ ، ومن ثم فإن:

$\frac{du}{dx}=4x^3 \Rightarrow dx=\frac{du}{4x^3}$

ثانيًا: أغير حدود التكامل:

الحد السفلي	الحد العلوي
$$\begin{gathered} x= -1 , u = x^4+9 \\ u={(-1)}^4+9 \\ u=10 \end{gathered}$$	$$\begin{gathered} x= 0 , u = x^4+9 \\ u={\left(0\right)}^4+9 \\ u=9 \end{gathered}$$

 

 

 

 

 

 

 

ثالثًا: أستخدم طريقة التكامل بالتعويض لإيجاد الناتج:

بتعويض $u=1+x^4$ ، $dx=\frac{du}{4x^3}$                         ${\int }_{-1}^0\frac{x^3}{\sqrt{x^4+9}} dx={\int }_{10}^9 \frac{x^3}{\sqrt{u}} \times \frac{du}{4x^3}$

بالتبسيط واستخدام الصورة الأسية                         $$\begin{gathered} =\frac{1}{4}{\int }_{10}^9 u^{-\frac{1}{2}} du \\ =-\frac{1}{4}{\int }_9^{10} u^{-\frac{1}{2}} du \end{gathered}$$ 

 

تكامل اقتران القوة المضروب بثابت        $=-\frac{2}{4}{u}^{\frac{1}{2}} \overline{)\begin{array}{c}10\\ 9\end{array}}=-\frac{1}{2}{u}^{\frac{1}{2}} \overline{)\begin{array}{c}10\\ 9\end{array}}$

بالتعويض في الصورة الجذرية             $=-\frac{1}{2}\left(\sqrt{10}-\sqrt{9}\right)$

بالتبسيط                          $=-\frac{1}{2}\left(\sqrt{10}-3\right)=\frac{3-\sqrt{10}}{2}$

---

                   $3) {\int }_0^1 x e^{4x^2+3} dx$

أولًا: أفترض أنّ $u=4x^2+3$ ، ومن ثم فإن:

$\frac{du}{dx}=8x \Rightarrow dx=\frac{du}{8x}$

ثانيًا: أغير حدود التكامل:

الحد السفلي	الحد العلوي
$$\begin{gathered} x= 0 , u =4x^2+3 \\ u=4{\left(0\right)}^2+3 \\ u=3 \end{gathered}$$	$$\begin{gathered} x= 1 , u =4x^2+3 \\ u=4{\left(1\right)}^2+3 \\ u=7 \end{gathered}$$

 

 

 

 

 

 

 

ثالثًا: أستخدم طريقة التكامل بالتعويض لإيجاد الناتج:

بتعويض $u=4x^2+3$ ،$dx=\frac{du}{8x}$                            ${\int }_0^1 x e^{4x^2+3} dx={\int }_3^{7}x e^u \frac{du}{8x}$

بالتبسيط                                                                        $=\frac{1}{8}{\int }_3^7 e^u du$       

تكامل اقتران اللوغاريتم الطبيعي المضروب بثابت                $=\frac{1}{8}{e}^u \overline{)\begin{array}{c}7\\ 3\end{array}}$ 

بالتعويض                                                                          $=\frac{1}{8}\left(e^7-e^3\right)$

---

نهاية الدرس