رياضيات فصل ثاني

فكرة الدرس:

أجد الجذور التربيعية والتكعيبية للأعداد.

 

المصطلحات:

الجذر التربيعي، الجذر التكعيبي.

 

تعلم أنّ الجذر التربيعي للمُربع الكامل هو ذلك العدد الذي إذا ضُرب في نفسه فيُعطي المُربع الكامل، ويرمز له بالرمز $\sqrt{}$

 

فالجذر التربيعي للعدد 16 هو 4 ؛ لأنّ (4 × 4 = 16) وبالرموز: $\sqrt{16} = 4$ ويُقرأ الجذر التربيعي للعدد 16

معلومة: الجذر التربيعي عملية عكسية لعملية تربيع العدد.

   $3^{2 }= 9 \leftrightarrow \sqrt{9} = 3 \stackrel{\mathrm{مثال}}{\leftarrow }$

 

أما الجذر التكعيبي للمُكعّب الكامل هو ذلك العدد الذي إذا ضُرب في نفسه ثلاث مرات فيُعطي المُكعب الكامل، ويرمز له بالرمز  $\sqrt[3]{}$

 

فالجذر التكعيبي للعدد 27 هو 3 ؛ لأنّ (3 × 3 × 3 = 27) وبالرموز: $\sqrt[3]{27} = 3$ ويُقرأ الجذر التكعيبي للعدد 27

معلومة: الجذر التكعيبي عملية عكسية لعملية تكعيب العدد.

$2^3 = 8 \leftrightarrow \sqrt[3]{8} = 2 \stackrel{\mathrm{مثال}}{\leftarrow }$

 

مثال

جد قيمة كل ممّا يأتي:

 $\mathit{a}\mathbf{)}\mathbf{ }\sqrt{25}=\sqrt{5\times 5}=5$              $\mathit{b}\mathbf{)} \sqrt[3]{64}=\sqrt[3]{4\times 4\times 4}=4$             $\mathit{c}\mathbf{)}\mathbf{ }\sqrt[3]{-1000}=\sqrt[3]{-10\times -10\times -10}=-10$

---

يُمكن استعمال التحليل والأسس لإيجاد الجذور التربيعية والتكعيبية للأعداد الكبيرة.

أولًا: الجذور التربيعية

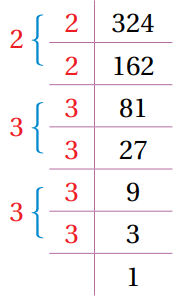
نحلل العدد إلى عوامله الأولية، ونأخذ عاملًا من كُل تكرارين له، ثم نحسب قيمة الجذر التربيعي.

 

مثال

جد قيمة $\sqrt{324}$

الحل:

الجذر التربيعي يُساوي ناتج ضرب العوامل التي تم أخذها.
$\sqrt{324}=2\times 3\times 3=18$

 

ثانيًا: الجذور التكعيبية

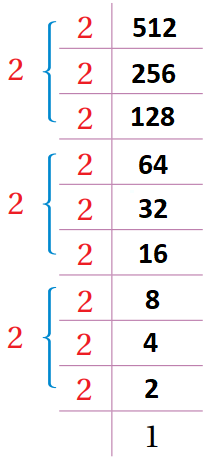
نحلل العدد إلى عوامله الأولية، ونأخذ عاملًا من كُل ثلاثة تكرارات له، ثم نحسب قيمة الجذر التكعيبي.

 

مثال

جد قيمة كلّ مما يأتي:  $\sqrt[3]{512}$     ،    $\sqrt[3]{-2744}$

الحل:

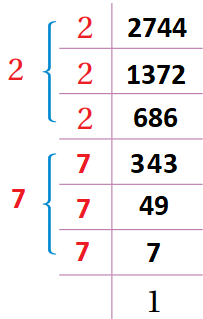
الجذر التكعيبي يُساوي ناتج ضرب العوامل التي تم أخذها.			1- نجد القيمة المطلقة للعدد - 2744 وهي 2744، ونقوم بتحليلها إلى عواملها الأولية.
$\sqrt[3]{512}=2\times 2\times 2=8$			2- نجد الجذر التكعيبي للعدد 2744 وهو يساوي ناتج ضرب العوامل التي تم أخذها.
			$\sqrt[3]{2744}=2\times 7=14$
			3- نضع الإشارة السالبة في ناتج الجذر التكعيبي النهائي.
			$\sqrt[3]{-2744}=-14$

---

تُستعمل الجذور التربيعية في كثير من المواقف الحياتيّة والعلميّة التي تحتوي مُضاعفة لعدد من الأشياء.

مثال

صَنعت فنانة لوحة خشبية مُربعة الشكل، مساحتها cm² 1089 ، جد طول ضلع اللوحة.

الحل:

بما أنّ اللوحة مُربعة الشكل فإنّ طول ضِلعها يُساوي الجذر التربيعي لمساحتها.

نحلل العدد 1089 إلى عوامله الأولية ، ثم نأخذ عاملا من كل تكرارين له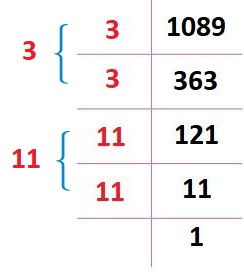
فيكون الجذر التربيعي (طول الضلع) يساوي ناتج ضرب العوامل المُختارة.
$\sqrt{1089}=3\times 11=33$
إذن، طول ضلع اللّوحة الخشبية 33 cm