الكسور المتكافئة 

هي كسور تمثل الكمية نفسها .

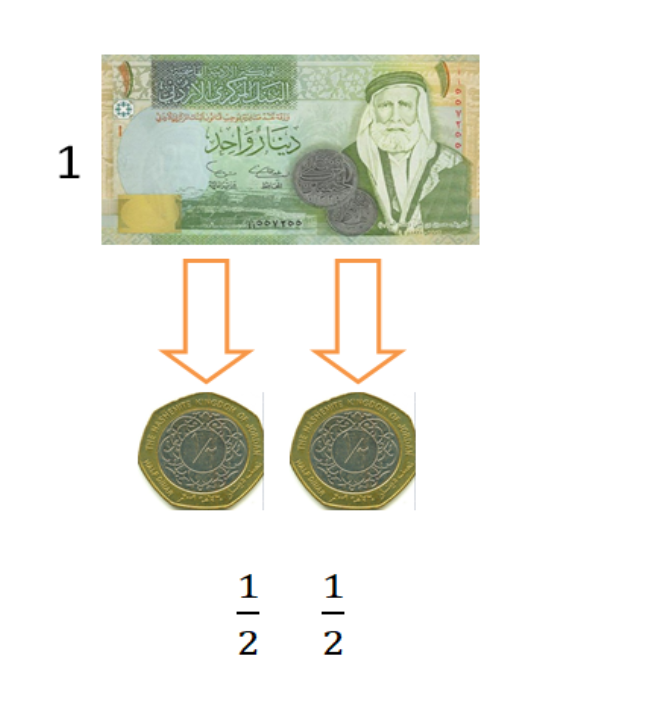
مثال (1): الدينار الأردني هو الوحدة الأساسية في هذا المثال ، إذا طلب منك الحصول على قطعتين لهما نفس قيمة الدينار سوف تذكر قطعتين من فئة النصف دينار ، لذلك فإن الدينار الأردني الذي يمثل وحدة واحدة يكافئ قطعتين من فئة النصف دينار .

                  

كذلك الدينار الأردني يكافئ (4) قطع من فئة الربع دينار 

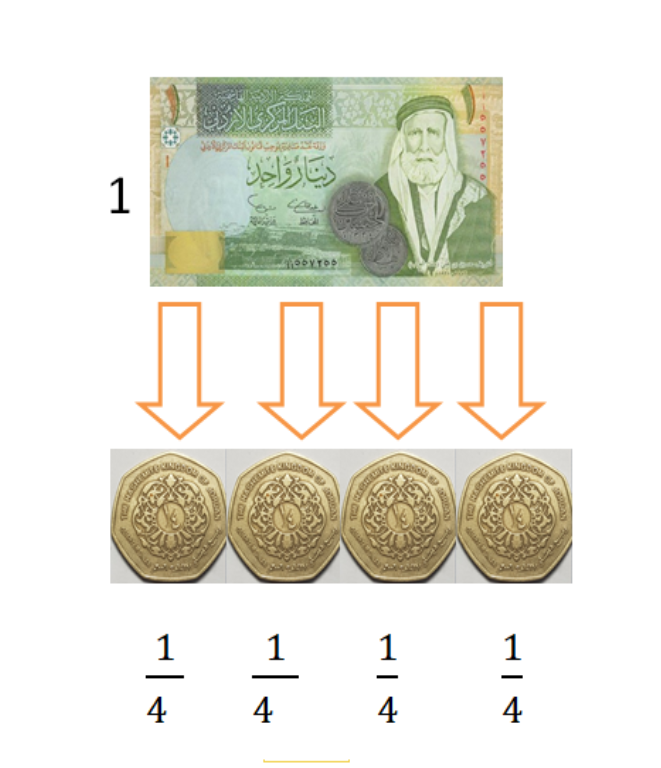
و النصف دينار يكافئ قطعتين من فئة الربع دينار  .

$\frac{2}{4}=\frac{1}{2}$   ( النصف يكافئ الربعين) 

يمكن الحصول على كسر مكافئ لكسر ما باستعمال عملية الضرب 

أضرب البسط و المقام في نفس العدد ما عدا العدد ( 1 ) 

مثال (2) : جد كسراً مكافئاً لكل كسر مما يأتي :

(( ضربنا البسط و المقام في 2 )) $\frac{1}{5}=\frac{ 2\times 1}{ 2\times 5}=\frac{ 2}{ 10}$   (1

                                     ((    الكسر $\frac{1}{5}$ يكافئ الكسر $\frac{2}{10}$  ))

(( الكسر $\frac{4}{7}$ يكافئ الكسر $\frac{12}{21}$))    $\frac{4}{7}=\frac{3\times 4}{3\times 7}=\frac{12}{21}$   (2 

-------------------------------------------------------------------------------------------------------------

مثال (3): جد العدد المفقود ليكون الكسران متكافئين :

 

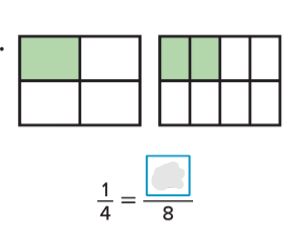
الكسر الذي يمثل الشكل الأيمن $\frac{2}{8}$  و الكسر الذي يمثل الشكل الأيسر $\frac{1}{4}$ نضع في الفراغ العدد (2)

 

 

 

---------------------------------------------------------------------------------------------------------------------                                          

يمكن الحصول على كسر مكافئ باستعمال عملية القسمة و ذلك بقسمة البسط و المقام على نفس العدد  و تسمى هذه العملية بالتبسيط 

مثال (4) : جد كسراً مكافئاً للكسر $\frac{5}{35}$ باستعمال عملية التبسيط :

(قسمنا البسط و المقام على العدد 5 لأن البسط 5 و المقام آحاده (5)) $\frac{5}{35}=\frac{5÷5}{35÷5}=\frac{1}{7}$

الكسر $\frac{1}{7}$ لا يمكن تبسيطه أكثر من ذلك و ذلك لأن العدد الوحيد الذي يمكن قسمة كل من البسط و المقام عليه هو العدد ( 1) فقط .

و يكون بذلك مكتوباً في أبسط صورة .

 

مثال (5) : جد كسراً مكافئاً لكل من الكسور الآتية باستعمال القسمة في أبسط صورة  : 

 $\frac{6}{24}=\frac{6÷2}{24÷2}=\frac{3÷3}{12÷3}=\frac{1}{4}$(1

 $\frac{8}{16}=\frac{8÷2}{16÷2}=\frac{4÷2}{8÷2}=\frac{2÷2}{4÷2}=\frac{1}{2}$(2

يمكنني أن أقسم  كلاً من البسط و المقام على العدد (8) مرة واحدة بدلاً من قسمتهما على العدد (2) ثلاث مرات 

$\frac{8÷8}{16÷8}=\frac{1}{2}$