المتتاليات

المتتاليات 

تعتبر المتتالية اقترانا مجاله مجموعة الأعداد الصحيحة الموجبة ، أو مجموعة جزئية منها و مداه مجموعة جزئية من مجموعة الأعداد الحقيقية .

---

مراجعة مفهوم 

المتتالية : هي مجموعة من الأعداد تتبع ترتيبًا معينا ويسمى كل عدد فيها حدًا

مثال :

أجد الحدود الثلاثة التالية لكل متتالية مما يأتي :

1) 2 , 4 , 6 , 8 , .....

بطرح أي حدين متتالين نجد أن كل حد يزيد عن الحد السابق بمقدار 2

إذا تتزايد المتتالية بمقدار 2

فالحدود الثلاثة التالية هي 

$2 , 4 , 6 , 8 , 10 , 12 , 14$

2) 5 , 10 , 20 , 40 , ...

بقسمة أي حدين متتالين نجد أن الحصول على أي حد يكون بضرب الحد السابق له بالعدد 2

إذا تتضاعف المتتالية بمقدار 2

فالحدود الثلاثة التالية هي

$5 , 10 , 20 , 40 , 80 , 160 , 320$

---

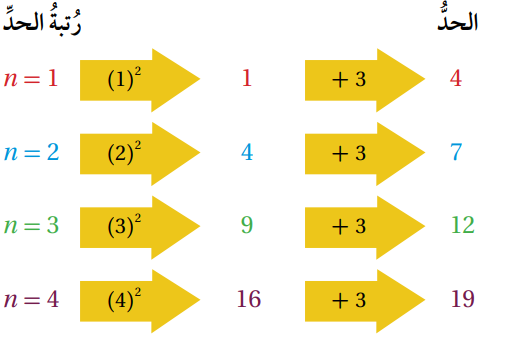
• تعلمنا في صفوف سابقة الحد العام لمتتالية الذي يمثل العلاقة بين اي حد ورتبته (n) و يرمز لع بالرمز T(n)   يسهل الحد العام ايجاد اي حد في المتتالية باستعمال رتبته  مثل الحد الذي رتبته خمسون مثلا و يمكن تصنيف المتتالية اعتمادا على حدها العام الى خطية و تربيعية وتكعيبية  وغير ذلك .

مثال 

أبين إذا كان المقدار الجبري المعطى بجانب كل متتالية مما يأتي يمثل حدًا عامًا لها أو لا ، ثم أصنف المتالليات إلى خطية أة تربيعية أو تكعيبية ثم أجد الحد الخامس والعشرين  في كل منها :

4 , 7 , 12 , 19 , ... , n² +3

أعوض للتأكد أن الحدود تنتج من الحد العام :

---

• يمكن إيجاد الحد العام للمتتاليات الخطية و التربيعية  والتكعيبية بملاحظة العلاقة بين الحدود ورتبها .

مثال

أجد الحد العام لكل متتالية مما يأتي : 

1)5 , 12 , 19 , 26 , 33 , ... 

الاحظ أن حدود المتتالية تتزايد بمقدار 7 : 

$5 , 12 , 19 , 26 , 33 , ...$

يمكن مبدئيا التعبير عن المتتالية بالحد 7n  لأن تزايد حدود المتتالية بمقدار 7 في كل مرة  ولكن عند تعويض  n = 1  ينتج العدد 7 و هو أكبر من الحد الأول بمقدار 2 ؛ لذا أطرح العدد 2 من 7n  وبذلك يصبح الحد العام 

T(n) = 7n - 2     

2)0 , 7 , 26 , 63 , 124 , ....

ألاحظ أن الفرق بين كل حدين  متتالين غير ثابت .

إذا المتتالية غير ناتجة من جمع ( أو طرح) عدد ثابت لحدودها .

ألاحظ أيضا أن المتتالية غير ناتجة من ضرب حدودها في عدد ثابت ، و أنها غير ناتجة من تربيع كل حد. أفسر المتتالية عن طريق تكعيب كل حد:

1        8       27     64    125       .... n³ 

0       7    26      63     124        .... ?  

 

 ألاحظ أنه عند طرح 1 من مكعب رتبة كل حد تنتج المتتالية المطلوبة .

لذلك فإن الحد العام هو 

T(n) = n³ - 1 

---

• تظهر المتتاليات في كثير من الأنماط الهندسية 

​​​​​​​مثال

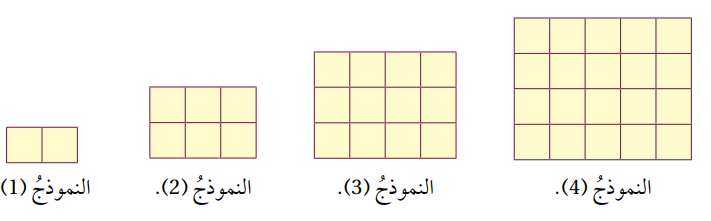
في ما يأتي نمط هندسي يمثل عدد المربعات في نماذجه متتالية . أجد الحد العام لهذه المتتالية .

بالنظر إلى النمط ألاحظ أن عدد المربعات يشكل المتتالية الآتية  ..... 20 , 12 , 6 , 2

بالنظر إلى الحدود الأولى من المتتالية ، ألاحظ أن كل حد فيها يساوي حاصل ضرب عرض المستطيل في طوله .

$$\begin{gathered} 2 \to 1\left(2\right) \\ 6 \to 2\left(3\right) \\ 12 \to 3\left(4\right) \\ 20 \to 4\left(5\right) \end{gathered}$$

إذا الحد العام هو

T(n) = n ( n+1)

---