النهايات والاتصال

فكرة الدرس: إيجاد نهاية اقتران عند قيمة مُحدّدة عدديًا وبيانيًا وجبريًا ، وبحث اتصال اقتران عند نقطة ما.            

أولًا :  إيجاد نهاية اقتران عند قيمة محددة عدديا وبيانيا وجبريا

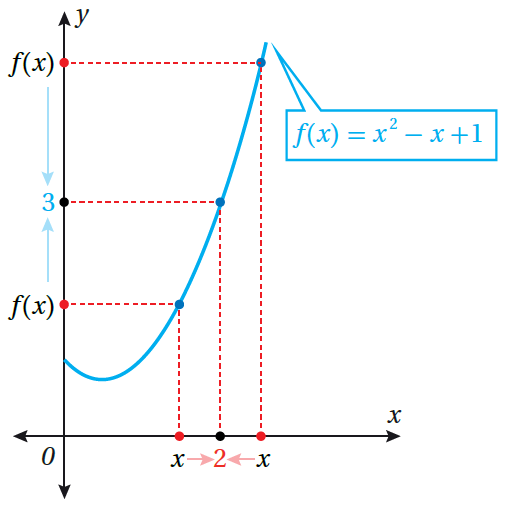
إذا كان الاقتران :    $f\left(x\right) = x^2 - x + 1$ ،  واخترتُ قِيَمًا للمُتغيّر  x  تقترب أكثر فأكثر من العدد 2 ، فإنني ألاحظ من جدول القِيم والتمثيل البياني التالي أنّه كلما اقتربت قِيم  x  من العدد  2 من جهة اليسار اقتربت قِيم الاقتران    f (x) من العدد  3 ، وأنه كلما اقتربت قِيم  x من العدد 2 من جهة اليمين اقتربت قِيم الاقتران من العدد  3، وبذلك فإنَّ نهاية

 ( limit )  الاقتران  f عند اقتراب  x  من العدد 2 من جهتي اليمين واليسار هي   3 ،  وتُكتب كما يأتي: $\underset{x\to 2}{\lim }(x^2- x + 1) = 3$ 

مفهوم أساسي (النهاية عند نقطة)

بالكلمات : إذا اقتربت قيمة الاقتران ( f(x من قيمة واحدة L عند اقتراب x من c، فإنَّ نهاية الاقتران ( f(x هي L عند اقتراب x من c. بشرط أن الاقتران معرّف في فترة مفتوحة حول c.

بالرموز  :  $\underset{x\to c}{\lim }f\left(x\right) = L$ 

وتُقرأ : نهاية الاقتران f(x) عند اقتراب x من c هي L.

 

يُشير الرمز $\underset{x\to c}{\lim }f\left(x\right) = L$  إلى اقتراب x  من c من جهتي اليمين واليسار .

لتحديد جهة اقتراب قِيم x من القيمة c :

• أستخدم الرمز  $\underset{x\to c^{-}}{\lim }f\left(x\right)$ للدلالة على النهاية من جهة اليسار ، حيث  $x<c$  ، وتُقرأ نهاية الاقتران f(x) عند اقتراب x من c من جهة اليسار. 

• أستخدم الرمز $\underset{x\to c^{+}}{\lim }f\left(x\right)$ للدلالة على النهاية من جهة اليمين ، حيث $x>c$ ،  وتُقرأ نهاية الاقتران f(x) عند اقتراب x من c من جهة اليمين. 

 

إذا كانت النهايتان من جهتي اليمين واليسار موجودتين ومتساويتين، فإنَّ نهاية الاقتران تكون موجودة.

 

مفهوم أساسي (النهاية من الجهتين)

بالكلمات : تكون نهاية الاقتران ( f(x موجودة عند اقتراب x من c إذا وفقط إذا كانت النهايتان من جهتي اليمين واليسار موجودتين ومتساويتين.

بالرموز  : $\underset{x\to c^{-}}{\lim }f\left(x\right) = \underset{x\to c^{+}}{\lim }f\left(x\right) = L \iff \underset{x\to c}{\lim }f\left(x\right) = L$

ملاحظة : يُقرأ الرمز  $(\iff )$ إذا وفقط إذا ، ويعني تحقق صحة عبارة الرياضيات في كلا الاتجاهين .

 

مثال 1 : 

أجد قيمة كل نهاية ممّا يأتي (إنْ وُجِدت) بيانيا وعدديا :

(1) $\underset{x\to 3}{\lim }f\left(x\right)$ ، حيث : $f\left(x\right) = x + 1$

الطريقة الأولى : إيجاد نهاية الاقتران بيانيا

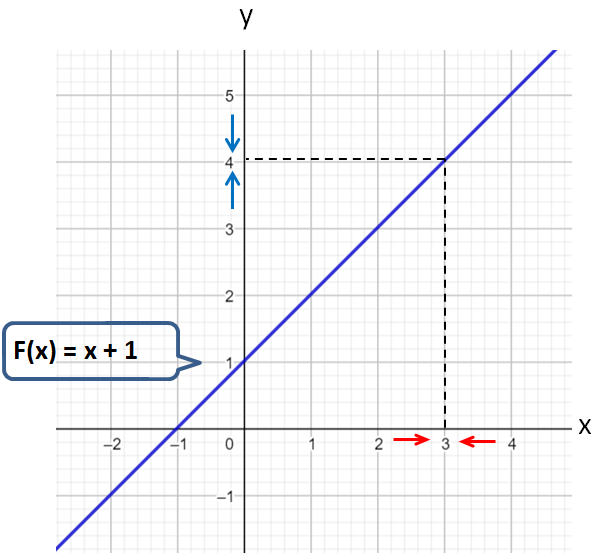
أُلاحظ من التمثيل البياني المجاور أنّه كلما اقتربت قيم x من العدد 3 من جهة اليمين اقتربت قِيم الاقتران (f(x المقابلة لها من العدد 4 ، وهذا يعني أنَّ :   $\underset{x\to 3^{+}}{\lim }f\left(x\right) = 4$ أُلاحظ أيضًا أنّه كلما اقتربت قِيم x من العدد 3 من جهة اليسار اقتربت قِيَم الاقتران  (f(x المقابلة لها من العدد 4 ، وهذا يعني أنّ : $\underset{x\to 3^{-}}{\lim }f\left(x\right) = 4$ بما أنّ النهايتين من جهتي اليمين واليسار متساويتان ، فإنّ نهاية الاقتران $\underset{x\to 3}{\lim }f\left(x\right)$ موجودة، وقيمتها 4.

 

 

 

 

 

 

 

 

 

 

 

                                                                                                       

الطريقة الثانية : إيجاد قيمة نهاية الاقتران عدديًا 

لإيجاد نهاية الاقتران f عدديًّا، أُنشئ جدول قيم باختيار قيم x القريبة من العدد 3 من كلتا
الجهتين ، ثم إيجاد قيم الاقتران (f(x المقابلة لها :     

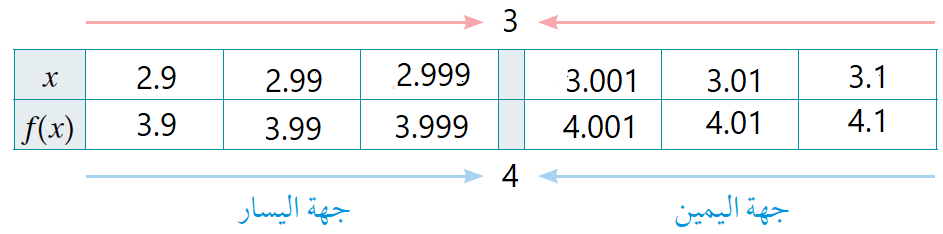
أُلاحظ من الجدول أنه كلما اقتربت قيم x من العدد 3 من جهة اليمين اقتربت قيم الاقتران(   f(x
المقابلة لها من العدد 4، وهذا يعني أن:  

$\underset{x\to 3^{+}}{\lim }f\left(x\right)= 4$

 وأُلاحظ أيضًا أنه كلما اقتربت قيم x من العدد 3 من جهة اليسار اقتربت قيم الاقتران(   f(x
المقابلة لها من العدد 4 ، وهذا يعني أن:  

 $\underset{x\to 3^{-}}{\lim }f\left(x\right) = 4$   

وبما أنّ $\underset{x\to 3^{+}}{\lim }f\left(x\right) = \underset{x\to 3^{-}}{\lim }f\left(x\right) = 4$ ، فإنّ نهاية الاقتران $\underset{x\to 3}{\lim f\left(x\right) }$ موجودة ، وقيمتها 4

---

 

(2) $\underset{x\to 1}{\lim }f\left(x\right)$ ، حيث : 

 $f\left(x\right) = \{\begin{array}{ll}3 ,& x \ge 1\\ 2x , & x < 1\end{array}$

 

الطريقة الأولى : إيجاد نهاية الاقتران بيانيا

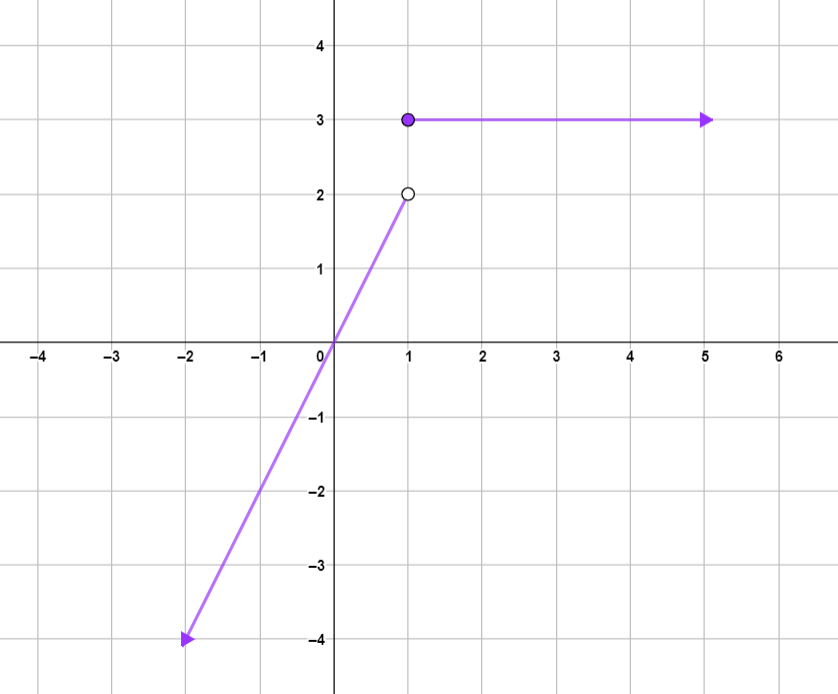
أُلاحظ من التمثيل البياني المجاور أنّه كلما اقتربت قيم x من العدد 1 من جهة اليمين اقتربت قِيم الاقتران (f(x المقابلة لها من العدد 3 ، وهذا يعني أنَّ :

$\underset{x\to 1^{+}}{\lim }f\left(x\right) = 3$

أُلاحظ أيضًا أنّه كلما اقتربت قِيم x من العدد 1 من جهة اليسار اقتربت قِيم الاقتران  (f(x المقابلة لها من العدد 2 ، وهذا يعني أنّ :

$\underset{x\to 1^{-}}{\lim }f\left(x\right) = 2$

بما أن $\underset{x\to 1^{+}}{\lim }f\left(x\right) \ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$ ، فإنّ $\underset{x\to 1}{\lim }f\left(x\right)$غير موجودة .

الطريقة الثانية : إيجاد قيمة نهاية الاقتران عدديًا 

لإيجاد نهاية الاقتران f عدديًّا، أُنشئ جدول قيم باختيار قيم x القريبة من العدد 1 من كلتا الجهتين ، ثم إيجاد قيم الاقتران (f(x المقابلة لها : 

أُلاحظ من الجدول أنه كلما اقتربت قيم  x من العدد 1 من جهةاليمين ، كانت قيم f(x)  
المقابلة لها تساوي  3 ، وهذا يعني أن:

$\underset{x\to 1^{+}}{\lim }f\left(x\right) = 3$

وأُلاحظ من الجدول  أنه كلما اقتربت قيم x من العدد 1 من جهةاليسار ، اقتربت قِيم الاقتران (f(x

المقابلة لها من العدد 2 ، وهذا يعني أن:

$\underset{x\to 1^{-}}{\lim }f\left(x\right) = 2$

بما أنّ $\underset{x\to 1^{+}}{\lim }f\left(x\right) \ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$ ، فإنّ $\underset{x\to 1}{\lim }f\left(x\right)$ غير موجودة.

---

إيجاد نهاية اقتران عند قيمة محددة جبريا

يُمكن إيجاد قيمة نهاية الاقتران لبعض الاقترانات البسيطة (مثل  : الاقتران الثابت ، والاقتران المحايد ) بسهولة دون الحاجة إلى استخدام الطريقة البيانية والطريقة العددية.

مفهوم أساسي  (نهايات الاقترانات)

نهاية الاقتران الثابت بالكلمات : نهاية الاقتران الثابت عند أيّ نقطة c هي القيمة الثابتة للاقتران. بالرموز :   $\underset{x\to c}{\lim }K = k$
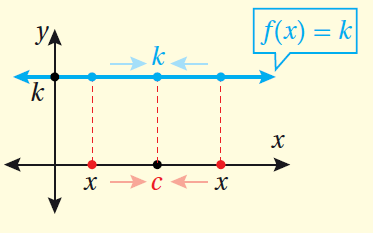نهاية الاقتران المحايد بالكلمات : نهاية الاقتران $f\left(x\right) = x$ عند النقطة c هي c بالرموز  : $\underset{x\to c}{\lim }x = c$

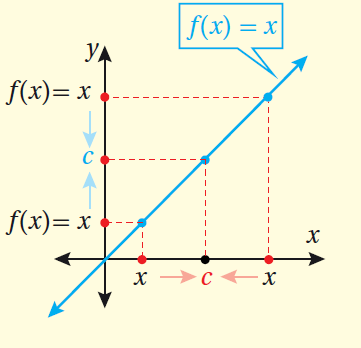يُمكن أيضًا استخدام الخصائص الجبرية للنهايات لإيجاد قِيم بعض النهايات من دون حاجة إلى استخدام الطريقة البيانية والطريقة العددية.

 مفهوم أساسي  (خصائص النهايات)

 إذا كان k , c عددين حقيقيين ، وكان n عددًا صحيحًا موجبًا ، وكانت النهايتان
$\underset{x\to c}{\lim }g\left(x\right)$ , $\underset{x\to c}{\lim }f\left(x\right)$ موجودتين، فإنّ كل من الخصائص الآتية صحيحة :

خاصية المجموع :	$\underset{ x\leftarrow c}{\mathbf{1}\mathbf{)} \lim }\left(f\right(x) + g(x\left)\right) = \underset{x\to c}{\lim }f\left(x\right) + \underset{x\to c}{\lim }g\left(x\right)$
خاصية الفرق :	$\mathbf{2}\mathbf{)}\mathbf{ }\underset{x\to c}{lim}(f\left(x\right) - g\left(x\right)) = \underset{x\to c}{lim}f(x) - \underset{x\to c}{lim g\left(x\right)}$
خاصية الضرب في ثابت :	$\mathbf{3}\mathbf{)}\mathbf{ }\underset{x\to c}{lim}K (f\left(x\right)) = K \underset{x\to c}{lim}f(x)$
خاصية الضرب :	$\mathbf{4}\mathbf{)} \underset{x\to c}{\lim }(f\left(x\right) \times g\left(x\right)) = \underset{x\to c}{\lim }f(x) \times \underset{x\to c}{\lim }g(x)$
خاصية القسمة :	$\mathbf{5}\mathbf{)} \underset{x\to c}{lim} \frac{f\left(x\right)}{g\left(x\right)} = \frac{\underset{\mathrm{x}\to \mathrm{c}}{\lim }\mathrm{f}\left(\mathrm{x}\right)}{\underset{\mathrm{x}\to \mathrm{c}}{\lim }\mathrm{g}\left(\mathrm{x}\right)} , \underset{\mathrm{x}\to \mathrm{c}}{\lim }g(x) \ne 0$
خاصية القوة :	$\mathbf{6}\mathbf{)}\mathbf{ }\underset{x\to c}{\lim }\mathbf{ }\mathbf{(}f{\mathbf{\left(}x\mathbf{\right)}\mathbf{)}}^n\mathbf{ }=\mathbf{ }(\underset{x\to c}{lim}f{\left(x\right))}^n$
خاصية الجذر النوني : إذا كان n عددًا زوجيًا ، فأتحقق من أنّ : $\underset{x\to c}{\lim }f\left(x\right) \ge 0$	$\mathbf{7}\mathbf{)} \underset{x\to c}{\lim }\sqrt[n]{f\left(x\right) } = \sqrt[n]{\underset{x\to c}{\lim }f\left(x\right)}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال :

أستخدم خصائص النهايات لإيجاد قيمة كل نهاية ممّا يأتي :

  $\mathbf{1}\mathbf{)}\mathbf{ }\underset{\mathbf{x}\mathbf{\to }\mathbf{2}}{\mathbf{l}\mathbf{i}\mathbf{m}\mathbf{(}}{\mathbf{x}}^{\mathbf{3}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{2}\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{6}\mathbf{)}$

           $\underset{x\to 2}{\lim (}{x}^3 + 2x - 6)$

 

خاصيتا الجمع والفرق	$=\underset{x\to 2}{\lim }\left(x^3\right) + \underset{x\to 2}{\lim }\left(2x\right) - \underset{x\to 2}{\lim }\left(6\right)$
خاصيتا القوة والضرب في ثابت	$= {\left(\underset{x\to 2}{\lim }x\right)}^3 + 2 \times \underset{x\to 2}{\lim (}x) - \underset{x\to 2}{\lim }(6)$
نهاية الاقتران المحايد ، ونهاية الاقتران الثابت	$= {\left(2\right)}^3 + 2 \times 2 - 6$
بالتبسيط	$= 6$

 

 

 

 

 

 

$\mathbf{2}\mathbf{)}\mathbf{ }\underset{\mathbf{x}\mathbf{\to }\mathbf{3}}{\mathbf{l}\mathbf{i}\mathbf{m}}\mathbf{ }\sqrt{\mathbf{ }\frac{{\mathbf{x}}^{\mathbf{2}}\mathbf{+}\mathbf{ }\mathbf{3}}{\mathbf{2}\mathbf{x}}}$

  $\mathbf{ }\mathbf{ }\underset{\mathrm{x}\to 3}{\lim }\mathbf{ }\sqrt{ \frac{ {\mathrm{x}}^2+ 3}{2\mathrm{x}}}$

خاصية الجذر النوني	$= \sqrt{\underset{x\to 3}{\lim }\frac{x^{2 }+ 3}{2x}}$
خاصية القسمة	$= \sqrt{\frac{\underset{x\to 3}{\lim }{x}^2+3}{\underset{x\to 3}{\lim }2x}}$
خاصية المجموع	$= \sqrt{\frac{\underset{x\to 3}{\lim }{x}^2 + \underset{x\to 3}{\lim }3}{\underset{x\to 3}{\lim }2x} }$
خاصية القوة ، وخاصية الضرب في ثابت	$=\sqrt{\frac{{\left(\underset{x\to 3}{\lim }x\right)}^2 + \underset{x\to 3}{\lim }\left(3\right)}{2 \times \underset{x\to 3}{\lim }\left(x\right)}}$
نهاية الاقتران المحايد ونهاية الاقتران الثابت	$=\sqrt{\frac{{\left(3\right)}^2 + 3}{ 2 \times 3 }}$
بالتبسيط	$= \sqrt{2}$

 

 

 

 

 

        

 

 

 

 

 

 

 

 

 

 

---

يمكن إيجاد نهاية الاقترانات كثيرات الحدود بالتعويض المباشر في الاقتران للقيمة التي تقترب منها(x) . ويُمكن إيجاد النهاية للاقترانات النسبية كذلك بالتعويض المباشر ، ولكن بشروط مُحددة .

مفهوم أساسي (النهايات بالتعويض المُباشر)

نهايات كثيرات الحدود
إذا كان الاقتران (f(x كثير حدود ، وكان c عددًا حقيقيًّا ، فإنّ : $\underset{x\to c}{\lim } f\left(x\right) = f\left(c\right)$

 نهايات الاقترانات النسبية 

إذا كان : $f\left(x\right) = \frac{p\left(x\right)}{q\left(x\right)}$ اقترانًا نسبيًا ، وكان c عددًا حقيقيًا ، فإنّ : $\underset{x\to c}{\lim }f\left(x\right) = f\left(c\right) = \frac{p\left(c\right)}{q\left(c\right)} , q\left(c\right) \ne 0$

 

تنبيه : ( يُمكِن إيجاد نهاية الاقتران النسبي بالتعويض المباشر ما دامت قيمة مقام الاقتران النسبي عند c لا تساوي صفرًا.)

 

مثال : 

أجد قيمة كل نهاية ممّا يأتي باستخدام التعويض المباشر إنْ كان ذلك مُمكِنًا. 

$\mathbf{1}\mathbf{)}\mathbf{ }\underset{\mathbf{x}\mathbf{\to }\mathbf{2}}{\mathbf{l}\mathbf{i}\mathbf{m}}\mathbf{(}{\mathbf{x}}^{\mathbf{4}}\mathbf{-}\mathbf{ }\mathbf{3}\mathbf{x}\mathbf{ }\mathbf{+}\mathbf{1}\mathbf{)}$

الاقتران  $f\left(x\right) = x^4- 3x + 1$ كثير حدود ، لذا يُمكن إيجاد قيمة نهايته بالتعويض المباشر بـ $(x = 2)$ :

$\underset{x\to 2}{\lim }(x^4- 3x + 1)$

$=(2^4 - 3 \times 2 + 1)$

$= 11$

---

$\mathbf{2}\mathbf{)}\mathbf{ }\underset{\mathbf{x}\mathbf{\to }\mathbf{-}\mathbf{3}}{\mathbf{l}\mathbf{i}\mathbf{m}}\frac{{\mathbf{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{3}}{\mathbf{1}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{2}\mathit{x}\mathbf{ }}$

  ألاحظ عند تعويض $(x = -3)$ في المقام فالناتج = (7 ) ، وهذا يعني أن  $(x = - 3)$ ليست صفرًا للمقام ، إذن يُمكن إيجاد نهاية الاقتران بالتعويض المباشر  : 

$\underset{\mathrm{x}\to -3}{lim}\frac{{\mathrm{x}}^2 + \mathrm{x} - 3}{1 - 2x} = \frac{{(-3)}^{2 }+ (-3) - 3}{1 - 2(-3)}$

  $= \frac{9 - 3 - 3}{1 + 6}$   

  $= \frac{3}{7}$

  

---

$\mathbf{3}\mathbf{)}\mathbf{ }\underset{\mathbf{x}\mathbf{\to }\mathbf{4}}{\mathbf{l}\mathbf{i}\mathbf{m}}\frac{{\mathbf{x}}^{\mathbf{2}}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{16}}{\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{4}}$

عند تعويض  x  =  4  في مقام الكسر فإن الناتج = صفر  ، وهذا يعني أن 4  =  x  لا تقع في مجال الاقتران النسبي ؛ لذا يتعذر إيجاد نهاية الاقتران بالتعويض المباشر  .   
 

---

الصيغة غير المحددة 

تظهر الصيغة غير المحددة أحيانًا عند التعويض المباشر  للقيمة التي تقترب منها (x ) في نهاية الاقتران النسبي ، فيكون الناتج $\frac{0}{0}$ ، وهذا لا يعني أنّ النهاية غير موجودة ، فمثلًا : التعويض المباشر  لقيمة $(x = 3)$ في $\underset{x\to 3}{\lim }\frac{x^2- 4x + 3}{x - 3}$ يُعطي  $\frac{0}{0}$ ، لكن التمثيل البياني للاقتران يُبين أنّ النهاية عندما تقترب x  من العدد 3 موجودة، وقيمتها  2 ، لذا يجب إيجاد صيغة مكافئة للاقتران عن طريق تحليل البسط ، أو تحليل المقام ، أو تحليل كليهما ، ثم اختصار العوامل المشتركة بينهما للتخلص من صفر المقام قبل التعويض.

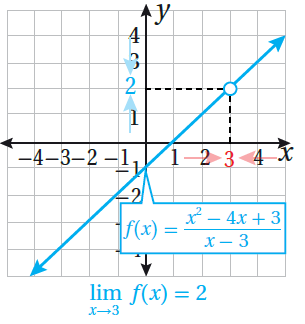 مثال : 

أجد قيمة   $\underset{\mathrm{x}\to 1}{\lim }\frac{{\mathrm{x}}^2+ 4\mathrm{x} - 5}{2\mathrm{x} - 2}$

ناتج التعويض المباشر في الاقتران النسبي هو $\frac{0}{0}$ ؛ لذا أُحلِّل المقدار جبريًّا ، ثم أختصر العوامل المشتركة بين البسط والمقام	$\underset{\mathrm{x}\to 1}{\lim }\frac{{\mathrm{x}}^2+ 4\mathrm{x} - 5}{2\mathrm{x} - 2}$
تحليل البسط والمقام إلى العوامل الأولية	$\underset{\mathrm{x}\to 1}{\lim }\frac{{\mathrm{x}}^2+ 4\mathrm{x} - 5}{2\mathrm{x} - 2} = \underset{x\to 1}{\lim }\frac{(x + 5) (x - 1)}{2 (x - 1)}$
اختصار العوامل المشتركة بين البسط  والمقام	$= \underset{x\to 1}{\lim }\frac{(x + 5)\cancel{ (x - 1)}}{2 \cancel{(x - 1)}}$
بالتبسيط	$= \underset{x\to 1}{\lim }\frac{x + 5}{2}$
بالتعويض المباشر والتبسيط	$= \frac{1+5}{2} = 3$

 

 

 

 

 

 

 

 

 

 

 

 

 

---

ثانيًا : بحث اتصال اقتران عند نقطة ما 

يكون الاقتران متصلًا  ( continuous function ) إذا لم يكن في تمثيله البياني أيُّ انقطاع ، أو فجوة ، أو قفزة. وكذلك يكون
الاقتران متصلًا عند نقطة ما تقع على منحناه إذا مرّ هذا المنحنى بتلك النقطة من دون انقطاع.

تشير التمثيلات البيانية الآتية إلى حالات من اتصال بعض الاقترانات أو عدم اتصالها عندما x = 1

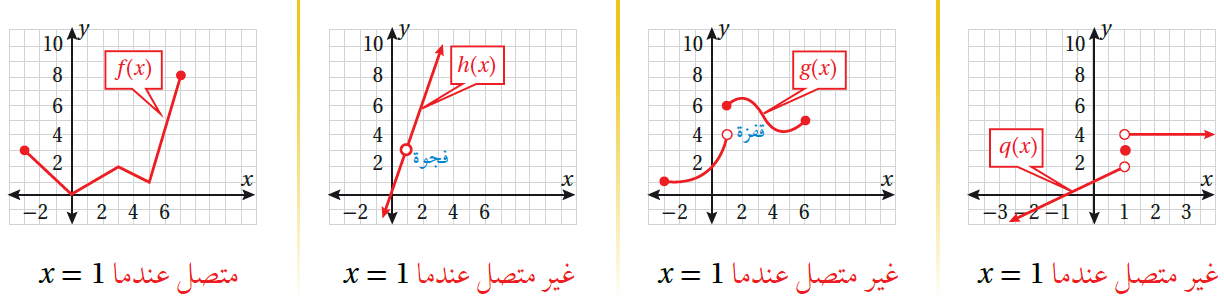
ألاحظ أنّ منحنى الاقتران h غير متصل عندما x = 1 ؛ لأنّه غير مُعرّف عندها (بالرغم من أنّ نهاية الاقتران h موجودة عند
اقتراب x من العدد 1) .

أمّا الاقترانان g و q فغير متصلين عندما x = 1 ؛ نظرًا إلى وجود قفزة في منحنى كلّ منهما ؛ ما يعني أنّ النهاية غير موجودة عند اقتراب x من العدد 1 (بالرغم من أنّ كُلّ منهما مُعرّف عندما x = 1 ) ، في حين يظهر الاقتران f متصلًا عندما x = 1 ، ويكون مُعرَفًا عندما x = 1 ، حيث : 1 = (f(1 ، وكذلك توجد له نهاية عند اقتراب x من العدد 1 ، حيث :

 $\underset{x\leftarrow 1}{\lim }f\left(x\right) = 1$ 

إذن ، يكون الاقتران متصلًا عند نقطة ما إذا كانت قيمة نهايته تساوي صورة الاقتران عند هذه النقطة. 

---

 مفهوم أساسي  (الاتصال عند نقطة) 

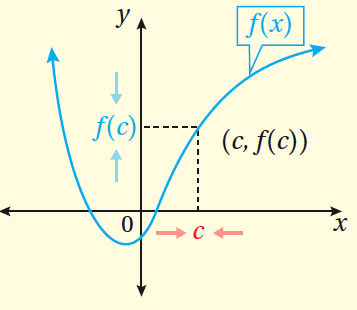
يكون الاقتران f(x) متصلًا عند  x  =  c  ، إذا حقق الشروط الآتية جميعها :                    • $f\left(c\right)$ موجودة .  • $\underset{x\to c}{\lim }f\left(x\right)$ موجودة . • $\underset{x\to c}{\lim }f\left(x\right) = f\left(c\right)$

مثال : 

أُحدّد إذا كان كل اقتران ممّا يأتي متصلًا عند قيمة x المعطاة ، مُبررًا إجابتي : 

الحل:	$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{ }\mathit{f}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }{\mathit{x}}^{\mathbf{3}}\mathbf{+}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathit{x}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{2}$
الخطوة (1)  : أجد قيمة الاقتران عندما $x = 2$ بالتعويض في الاقتران والتبسيط	$f\left(2\right) = 2^3 + 2 + 1 = 11$
الخطوة (2) : أجد قيمة نهاية الاقتران عندما تقترب x  من العدد 2	$\underset{x\to 2}{\lim }f\left(x\right) = \underset{x\to 2}{\lim }(x^3+ x + 1) = 11$
الخطوة (3) :  أقارن f(2) بـ $\underset{x\leftarrow 2}{\lim }f\left(x\right)$ القيمتان متساويتان.   إذن الاقتران f(x) متصل عند  x = 2	$\underset{x\to 2}{\lim }f\left(x\right) = f\left(2\right)$

                                                                                

 

 

 

 

 

 

 

 

 

 

 

---

 

الاقتران النسبي f(x)  غير مُعرف عند  x = 3  ؛ لأنّ ذلك يجعل مقامه يساوي صفرًا  . لذا f(x) غير متصل عند x = 3

$\mathbf{2}\mathbf{)}\mathbf{ }\mathit{f}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{9}\mathbf{ }\mathbf{-}\mathbf{ }{\mathbf{x}}^{\mathbf{2}}}{\mathbf{3}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{x}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{x}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{3}$

 

 

 

---

 

الحل:	$\mathbf{3}\mathbf{)}\mathbf{ }\mathit{f}\mathbf{(}\mathit{x}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{\{}\begin{array}{ll}{\mathbf{x}}^{\mathbf{2}}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{3}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }& \mathbf{x}\mathbf{ }\mathbf{\ge }\mathbf{ }\mathbf{4}\\ \mathbf{5}\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{1}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }& \mathbf{x}\mathbf{ }\mathbf{<}\mathbf{ }\mathbf{4}\end{array}\mathbf{ } \mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }\mathbf{ }\mathit{x}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{4}$
الخطوة (1)  : أجد قيمة الاقتران عند x = 4 بالتعويض في الاقتران والتبسيط.	$f\left(4\right) = 4^{2 }+ 3 = 19$
الخطوة (2) : أجد قيمة نهاية الاقتران عندما تقترب x  من العدد 4
النهاية من جهة اليمين	$\underset{x\to 4^{+}}{\lim }f\left(x\right) = \underset{x\to 4^{+}}{\lim }(x^2+ 3) = 19$
النهاية من جهة اليسار	$\underset{x\to 4^{+}}{\lim }f\left(x\right) = \underset{x\to 4^{+}}{\lim }(5x-1) = 19$
الخطوة (3) :  أقارن f(4) بـ  $\underset{x\leftarrow 4}{\lim }f\left(x\right)$
القيمتان متساويتان	$\underset{x\to 4}{\lim }f\left(x\right) = f\left(4\right)$
بما أنّ $f\left(4\right) = \underset{x\to 4}{\lim }f\left(x\right)$ ، فإن الاقتران f  متصل عند  x = 4