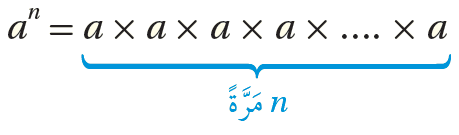رياضيات 9 فصل ثاني

تبسيطُ المقاديرِ الأُسِّيَّةِ

Simplifying Exponential Expressions

فكرةُ الدرسِ: استعمالُ خصائص الأُسس الصحيحة لتبسيطِ مقاديرَ أُسِّيَّةٍ.

 

أولًا : تبسيط المقاديرِ الأسِّيّة باستعمال خصائص ضرب القوى

تعلّمْتُ سابقا كيفَ أستعمل الأسسَ للتعبير عن الضرب المُتكرِّر لعدد في نفسه. وتعلَّمت أيضًا أنَّ عدد مَرّات تكرارِ الضربِ يُسمّى الأُسَّ، وأنّ العدد نفسهُ يُسمى الأساس، وأنَّ كُلّ منَ الأساس والأُسّ معا يُسمى القوَّة.

 

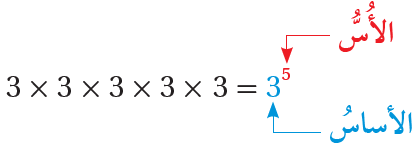
مراجعةُ المفهوم : الصيغة الأسِّيّة

إذا كانَ a عددًا حقيقيًّا، وكانَ n عددًا صحيحًا موجبًا، فإنَّ: حيث : a : الأساس. n : الأُسّ.

 

•• أتذكَّرُ : الصيغة الأُسّية هي صيغةٌ يُكتبُ فيها الضربُ المُتكرر باستعمال القوى.

 

تعلَّمْتُ أيضًا كيف أستعملُ خاصيةَ ضربِ القوى، وقوَّة القوَّة، وقوَّةِ ناتج الضرب إذا كانَ الأساس عددًا حقيقيًّا. والآن سأتعلَّم كيف أستعمل خصائص ضرب الأُسس هذهِ لتبسيط مقادير أُسِّية تحوي مُتغيرات.

 

مفهومٌ أساسيّ : خصائصُ ضربِ القوى

إذا كانَ a و b عددينِ حقيقيينِ أوْ مقدارينِ جبريينِ، وكانَ m و n عددينِ صحيحينِ، فإنَّ:

مثال		الخاصية
$z^2\times z^6=z^{2+6}=z^8$	ضربُ القوى	$a^m\times a^n=a^{m+n}$
${\left(h^3\right)}^{{}^2}=h^{3\times 2}=h^6$	قوَّةُ القوَّةِ	${\left(a^m\right)}^n=a^{mn}$
${\left(5w\right)}^3=5^3{w}^3=125w^3$	قوَّةُ ناتجِ الضربِ	${\left(ab\right)}^m=a^m{b}^m$

 

•• يكونُ المقدارُ الأُسّيُّ في أبسط صورةٍ إذا توافرَتْ فيهِ شروطٌ مُعيَّنةٌ.

 

مفهوم أساسيّ : أبسطُ صورة للمقدار الأُسّيّ

يكونُ المقدار الأُسّيّ في أبسط صورة إذا توافرت فيه الشروط الآتية : · أنْ يظهر الأساس مَرّة واحدة فقط، وأن تكون الأُسس جميعُها موجبة.  · ألّا يتضمَّن المقدار قوّة القوّة. · أنْ تكون الكسور جميعُها في أبسط صورة.

 

•• أتعلَّمُ : كتابةُ المقدارِ الأُسِّيِّ في أبسطِ صورةٍ تتطلَّبُ كتابةَ مقدارٍ مُكافِئٍ للمقدارِ الأُسِّيِّ، تتوافرُ فيهِ الشروطُ الواردةُ في الصندوقِ أعلاه.

مثال 1 : 

أكتب كُلًّا ممّا يأتي في أبسط صورة :

 

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{2}{\mathbf{x}}^{\mathbf{2}}\mathbf{ }{\mathbf{y}}^{\mathbf{ }}\mathbf{\left)}\mathbf{\right(}\mathbf{3}{\mathbf{x}}^{\mathbf{4}}\mathbf{ }{\mathbf{y}}^{\mathbf{3}}\mathbf{ }\mathbf{)}$

$(2f^2 y^{ })(3f^4 y^3 )=(2\times 3) (f^2\times f^4) (y\times y^3)$	بإعادةِ تجميعِ الثوابتِ والمُتغيِّراتِ
$= (2\times 3) (f^{2+4} ) \left(y^{1+3}\right)$	ضربُ القوى
$= 6 f^6{y}^4$	بالتبسيطِ

 

•• أتعلَّمُ : إذا لمْ يظهرْ أُسٌّ فوقَ المُتغيِّرِ، فإنَّ أُسَّهُ يكونُ 1 ؛ أيْ إنَّ : $y = y^1$

---

$\mathbf{2}\mathbf{)}\mathbf{ }\mathbf{(}{\mathbf{\left(}{\mathbf{a}}^{\mathbf{3}}\mathbf{\right)}}^{\mathbf{2}}{\mathbf{)}}^{\mathbf{4}}$

 

$({\left(a^3\right)}^2{)}^4 ={\left(a^{3\times 2}\right)}^4$	قوَّةُ القوَّةِ
$={\left(a^6\right)}^4$	بالتبسيطِ
$= a^{6\times 4}$	قوَّةُ القوَّةِ
$= a^{24}$	بالتبسيطِ

---

$\mathbf{3}\mathbf{)}\mathbf{ }{\mathbf{(}\mathbf{4}{\mathbf{b}}^{\mathbf{5}}\mathbf{ }{\mathbf{s}}^{\mathbf{6}}\mathbf{ }\mathbf{)}}^{\mathbf{3}}$

${(4b^5 s^6 )}^3= {\left(4\right)}^3 {\left(b^5\right)}^3 {\left(s^6\right)}^3$	قوَّةُ ناتجِ الضربِ
$= 64 b^{15} s^{18}$	بالتبسيطِ

---

$\mathbf{4}\mathbf{)}\mathbf{ }\mathbf{(}\mathbf{2}{\mathit{y}}^{\mathbf{3}}{\mathit{n}}^{\mathbf{2}}\mathbf{)}{\mathbf{(}\mathbf{-}\mathbf{3}\mathbf{y}{\mathbf{n}}^{\mathbf{4}}\mathbf{ }\mathbf{)}}^{\mathbf{2}}$

$\left(2y^3{n}^2\right){(-3{\mathrm{yn}}^4)}^2=\left(2y^3{n}^2\right) {\left(\right(-3)}^2 {\left(y\right)}^2 {\left(n^4\right)}^2)$	قوَّةُ القوَّةِ
$= \left(2y^3{n}^2\right) (9 y^2{ n^8)}^{ }$	بالتبسيطِ
$= (2\times 9) (y^3\times y^2) (n^2\times n^8)$	بإعادةِ تجميعِ الثوابتِ والمُتغيِّراتِ
$= 18y^5{n}^{10}$	ضربُ القوى

 

---

ثانيًا: تبسيطُ المقاديرِ الأُسِّيَّةِ باستعمالِ خصائصِ قسمةِ القوى

تعلَّمْتُ سابقًا كيفَ أستعملُ خاصية قسمة القوى، وخاصية قوَّة ناتج القسمة إذا كانَ الأساسُ عددًا حقيقيًّا. والآنَ سأتعلَّمُ كيفَ

أستعملُ هاتينِ الخاصيتينِ اللتينِ هما منْ خصائصِ قسمةِ الأُسسِ لتبسيط مقادير أُسِّيَّة تحوي مُتغيِّرات.

 

مفهومٌ أساسيٌّ: خصائصُ قسمةِ القوى

إذا كانَ a و b عددينِ حقيقيينِ أوْ مقدارينِ جبريينِ، حيثُ: a ≠ 0 و b ≠ 0 ، وكانَ m و n عددينِ صحيحينِ، فإنَّ:

مثال		الخاصية
$\frac{b^8}{b^3}=b^{8-3}=b^5$	قسمةُ القوى	$\frac{a^m}{a^n}=a^{m-n}$
${\left(\frac{4}{s}\right)}^2=\frac{4^2}{s^2}=\frac{16}{s^2}$	قوَّةُ ناتجِ القسمةِ	${\left(\frac{a}{b}\right)}^m=\frac{a^m}{b^m}$

 

مثال 2 : 

أكتبُ كُلًّا ممّا يأتي في أبسطِ صورة ، علمًا بأنَّ أيًّا منَ المُتغيِّرات لا يساوي صفرًا : 

$\mathbf{1}\mathbf{)}\mathbf{ }\frac{{\mathbf{x}}^{\mathbf{5}}{\mathbf{y}}^{\mathbf{3}}}{{\mathbf{x}}^{\mathbf{2}}\mathbf{y}}\mathbf{ }$

$\frac{{\mathrm{x}}^5{\mathrm{y}}^3}{{\mathrm{x}}^2\mathrm{y}} = \left(\frac{{\mathrm{x}}^5}{{\mathrm{x}}^2}\right)\left(\frac{{\mathrm{y}}^3}{\mathrm{y}}\right)$	بإعادةِ تجميعِ المُتغيِّراتِ
$=\left(x^{5-2}\right) \left(y^{3-1}\right)$	قسمةُ القوى
$= x^{3 }{y}^2$	بالتبسيطِ

---

$\mathbf{2}\mathbf{)}\mathbf{ }{\mathbf{\left(}\frac{\mathbf{-}\mathbf{3}{\mathbf{n}}^{\mathbf{5}}}{{\mathbf{n}}^{\mathbf{2}}{\mathbf{a}}^{\mathbf{4}}}\mathbf{\right)}}^{\mathbf{3}}$

${\left(\frac{-3{\mathrm{n}}^5}{{\mathrm{n}}^2{\mathrm{a}}^4}\right)}^3= {\left(\frac{-3n^{5-2}}{a^4}\right)}^3$	قسمةُ القوى
$= {\left(\frac{-3n^3}{a^4}\right)}^3$	بالتبسيطِ
$= \frac{{(-3)}^3{\left(n^3\right)}^3}{{\left(a^4\right)}^3}$	قوَّةُ القوَّةِ
$=\frac{-27n^9}{a^{12}}$	بالتبسيطِ

---

ثالثًا: تبسيطُ المقاديرِ الأُسِّيةِ باستعمال خصائص الأُسّ الصفريّ والأُسّ السالبِ

تعلّمت سابقا أنّ أيّ عدد حقيقي غير الصفر مرفوعًا إلى الأُسّ صفرٍ يساوي 1، وأنَّ القوّة ذاتَ الأساس غير الصفريّ والأُسّ

السالب هي مقلوب القوَّة ذات الأساس غير الصفري والأُسِّ الموجب، والعكس صحيح. والآن سأتعلَّم كيف أستعمل هاتين

الخاصيتين لتبسيط مقادير  أُسِّية تحوي مُتغيّرات.

 

مفهومٌ أساسيٌّ : الأُسُّ الصفريُّ والأُسُّ السالبُ

إذا كان a عددًا حقيقيًّا أو مقدارًا جبريًّا، حيث : a ≠ 0 ، وكان n عددًا صحيحًا، فإنَّ :

مثال		الخاصية
${\left(3x^2\right)}^0=1 , x\ne 0$	الأُسُّ الصفريُّ	$a^0=1$
$g^{-7}=\frac{1}{g^7} , g\ne 0$	الأُسُّ السالبُ	$a^{-n}=\frac{1}{a^n}$

 

مثال 3 : 

أكتبُ كُلًّ ممّا يأتي في أبسطِ صورةٍ، علمًا بأنَّ أيًّا منَ المُتغيِّراتِ لا يساوي صفرًا:  

$\mathbf{1}\mathbf{)}\mathbf{ }\frac{\mathbf{6}{\mathbf{x}}^{\mathbf{7}}{\mathbf{y}}^{\mathbf{2}}}{\mathbf{3}{\mathbf{x}}^{\mathbf{4}}{\mathbf{y}}^{\mathbf{3}}}\mathbf{ }$

$\frac{6{\mathrm{x}}^7{\mathrm{y}}^2}{3{\mathrm{x}}^4{\mathrm{y}}^3}=\left(\frac{6}{3}\right)\left(\frac{{\mathrm{x}}^7}{{\mathrm{x}}^4}\right)\left(\frac{{\mathrm{y}}^2}{{\mathrm{y}}^3}\right)$	بإعادةِ تجميعِ المُتغيِّراتِ ذاتِ الأساسِ المُتشابِهِ
$= \left(\frac{6}{3}\right)(x^{7-4} )\left(y^{2-3}\right)$	قسمةُ القوى
$= \left(2\right) \left(x^{3 }\right) \left(y^{-1}\right)$	بالتبسيطِ
$= \left(2\right)\left(x^3\right)\left(\frac{1}{y}\right)$	تعريفُ الأُسِّ السالبِ
$= \frac{2x^3}{y}$	بالضربِ

---

$\mathbf{2}\mathbf{)}\mathbf{ }\frac{\mathbf{5}{\mathbf{a}}^{\mathbf{3}}{\mathbf{bc}}^{\mathbf{-}\mathbf{2}}}{\mathbf{3}{\mathbf{ac}}^{\mathbf{0}}}$

$\frac{5{\mathrm{a}}^3{\mathrm{bc}}^{-2}}{3{\mathrm{ac}}^0}=\frac{5{\mathrm{a}}^3{\mathrm{bc}}^{-2}}{3\mathrm{a} }$	$c^0=1$
$= \left(\frac{5}{3}\right) \left(\frac{a^3}{a}\right) \left(b\right)\left(c^{-2}\right)$	بإعادةِ تجميعِ المُتغيِّراتِ ذاتِ الأساسِ المُتشابِهِ
$= \left(\frac{5}{3}\right) (a^{3-1} ) \left(b\right)\left(c^{-2}\right)$	قسمةُ القوى
$= \left(\frac{5}{3}\right) \left(a^2\right) \left(b\right)\left(\frac{1}{c^2}\right)$	تعريفُ الأُسِّ السالبِ
$=\frac{5a^{2}b}{3c^2}$	بالضربِ

 

•• أتذكَّرُ : إذا كانَ a و b عددينِ حقيقيينِ أوْ مقدارينِ جبريينِ، حيثُ: a ≠ 0 و b ≠ 0 ، وكانَ m عددًا صحيحًا فإنَّهُ يُمكِنُ كتابةُ ${\left(\frac{a}{b}\right)}^{-m}$  بالصورةِ الآتيةِ : ${\left(\frac{b}{a}\right)}^m$

مثال: 

${\left(\frac{3}{5}\right)}^{-2}={{\left(\frac{5}{3}\right)}^2}^{ }=\frac{5^2}{3^2}=\frac{25}{9}$

---