الرياضيات فصل ثاني

الدرس الخامس: تكامل اقترانات خاصة

 

سنتعرف في درس تكامل الاقترانات الخاصة إلى:

إيجاد تكاملات تتضمن:

1. اقترانات أسية طبيعية.

2. اقترانات الجيب وجيب التمام

3. اقترانات اللوغاريتمات الطبيعية

4. اقترانات أساسية في صورة $f(ax+b)$

5. اقترانات في صورة $k \frac{f َ\left(x\right)}{f\left(x\right)}$

6. التكامل المحدود للاقترانات الخاصة.

 

 

أولًا: تكامل الاقتران الأسي الطبيعي ، واقتران الجيب، واقتران جيب التمام:

التكامل والاشتقاق عمليتان عكسيتان ؛ لذلك يمكن استخدام ما تعلمناه بالاشتقاق

لإيجاد صيغ مباشرة لتكامل اقترانات ناتجة من اشتقاق اقترانات مشهورة، مثل:

 

1. الاقتران الأسي الطبيعي$\left(e^x\right)$:           $\frac{d}{dx}\left(e^x\right)=e^x$    

2. اقتران جيب التمام$\left(\cos x\right)$ :     $\frac{d}{dx}(\cos x)=- \sin x$

3. اقتران الجيب $\left(\sin x\right)$:                  $\frac{d}{dx}(\sin x)=\cos x$

 

 

لذلك يمكن إيجاد صيغة تكامل كل من الاقترانات السابقة كالآتي:

                         

            

مثال(1): جد كلًا من التكاملات الآتية:

                   $$\begin{gathered} 1) \int \left(2-3e^x\right)dx \\ 2) \int \left(\sqrt[3]{x^2}-\cos x\right)dx \\ 3) \int \left(4\sin x + \frac{5}{x^4}\right) dx \end{gathered}$$

                

الحل:

$1) \int (2-3e^x)dx=2x -3e^x + C$

$$\begin{gathered} 2) \int (\sqrt[3]{x^2}-\cos x)dx=\int \left(x^{\frac{2}{3}}-\cos x\right) dx \\ = \frac{x^{{\displaystyle \frac{5}{3}}}}{{\displaystyle \frac{5}{3}}}-\sin x+ C \\ = \frac{3}{5}\sqrt[3]{x^5} -\sin x+ C \end{gathered}$$

$$\begin{gathered} 3) \int (4\sin x + \frac{5}{x^4}) dx = \int \left(4\sin x + 5 x^{-4}\right) dx \\ =-4\cos x +-\frac{5}{3} x^{-3} +C \\ = -4\cos x - \frac{5}{3x^3}+C \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

تذكر: إذا كان k ثابتًا، فإنّ:

$$\begin{gathered} \mathbf{1}\mathbf{.} \int k dx = kx + C \\ \mathbf{2}\mathbf{.} \int k f\left(x\right) dx = k \int f\left(x\right) dx \\ \mathbf{3}\mathbf{.} \int x^n dx = \frac{1}{n+1}{x}^{n+1} + C , n\ne -1 \end{gathered}$$

 

 

 

 

 

 

 

 

---

ثانيًا: تكامل الاقتران:$\frac{1}{x}$

تعلمت أنّ: $\frac{d}{dx}(\ln x) = \frac{1}{x}$ ، وبما أن التكامل والاشتقاق عمليتان عكسيتان فإنّ:

$\int \frac{1}{x} dx = \ln x +C$ .

ولكن بما أنّ:

1) $\ln x$ معرف فقط عندما يكون $x>0$، فإنّ: $\int \frac{1}{x} dx = \ln x +C$

2) $\ln (-x)$ معرف فقط عندما يكون $x<0$، فإنّ: $\int \frac{1}{x} dx = \ln \left(-x\right) +C$

وبدمج النتيجتين:(1) ، (2)  فإن قاعدة تكامل الاقتران اللوغاريتمي الطبيعي هي:

                     $\int \frac{1}{x} dx = \ln \left|x\right| +C, x\ne 0$

 

مثال(2): جد كلًا من التكاملات الآتية:

                     $$\begin{gathered} 1) \int (6x^2-\frac{1}{x}\left)dx \\ 2\right) \int (5\cos x+\frac{4}{x})dx \\ 3) \int (\frac{4x^3+ 5 x}{x^2}) dx \end{gathered}$$

الحل:

$1) \int (6x^2-\frac{1}{x})dx=\frac{6x^3}{3}-\ln \left|x\right|+C$

$2) \int (5\cos x+\frac{4}{x})dx = 5 \sin x +4\ln \left|x\right| +C$

$$\begin{gathered} 3) \int (\frac{4x^3+ 5 x}{x^2}) dx=\int \left(\frac{4x^3}{x^2} + \frac{5x}{x^2}\right) dx \\ =\int \left(4x + \frac{5}{x}\right) dx \\ = \frac{4x^2}{2}+5 \ln \left|x\right| +C \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

ثالثًا: تكامل اقترانات أساسية في صورة:$\mathit{f}\mathbf{(}\mathit{a}\mathit{x}\mathbf{+}\mathbf{ }\mathit{b}\mathbf{)}$

درست سابقًا اشتقاق الاقترانات الآتية:

1. اقتران القوة: $\frac{d}{dx}\left({\left(ax+b\right)}^n\right) = n a{(ax+ b)}^{n-1}$

2. الاقتران الأسي الطبيعي: $\frac{d}{dx}\left(e^{ax+b}\right) = a e^{ax+b}$

3. اقتران جيب التمام: $\frac{d}{dx}\left(\cos \left(ax + b\right)\right) = -a \sin (ax + b)$

4. اقتران الجيب :$\frac{d}{dx}\left(\sin \left(ax + b\right)\right) = a \cos (ax + b)$

 

والآن سنجد تكاملاتها إذا كانت في صورة $f(ax+ b)$:

إذا كان $a,b$ عددين حقيقيين، و $a\ne 0$ ،و $e$ هو العدد النيبيري فإن:  $$\begin{gathered} 1) \int {\left(ax +b\right)}^n dx = \frac{1}{a(n+1)}{\left(ax +b\right)}^{n+1}+C , n\ne -1 \\ 2) \int e^{ax+b} dx = \frac{1}{a}{e}^{ax+b} +C \\ 3) \int \sin (ax+b) dx = -\frac{1}{a}\cos (ax+ b) +C \\ 4) \int \cos (ax+b) dx = \frac{1}{a} \sin (ax+ b) +C \\ 5) \int \frac{1}{ax + b} dx = \frac{1}{a} \ln \left|ax+b\right| +C, x\ne -\frac{b}{a} \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال(3): جد كلًا من التكاملات الآتية:

                                                                                                                                    $$\begin{gathered} 1) \int {(9-8x)}^7 dx \\ 2) \int \sqrt[3]{(10x - 5)}dx \\ 3) \int (8x^3-5e^{6x-7}) dx \\ 4) \int 2\cos (4x+11) dx \\ 5) \int (\sin 9x+\frac{4}{5x-2}) dx \end{gathered}$$

 

الحل:

$$\begin{gathered} 1) \int {(9-8x)}^7 dx =\frac{1}{\left(-8\right)}\times \frac{1}{8}{(9-8x)}^8+C \\ =-\frac{1}{64}{(9-8x)}^8+C \end{gathered}$$

$$\begin{gathered} 2) \int \sqrt[3]{(10x - 5)}dx= \int {(10x - 5)}^{\frac{1}{3}} dx \\ =\frac{1}{10}\times \frac{1}{{\displaystyle \frac{4}{3}}}{(10x - 5)}^{\frac{4}{3}}+C \\ =\frac{3}{40}{(10x - 5)}^{\frac{4}{3}}+C \\ =\frac{3}{40}\sqrt[3]{}+C \end{gathered}$$

$$\begin{gathered} 3) \int (8x^3-5e^{6x-7}) dx=\frac{8 x^4}{4}-\frac{5}{6} e^{6x}+C \\ = 2 x^4-\frac{5}{6} e^{6x}+C \end{gathered}$$

$$\begin{gathered} 4) \int 2\cos (4x+11) dx = 2 \left(\frac{1}{4}\right) \sin (4x+11) +C \\ = \frac{1}{2}\sin (4x+11) +C \end{gathered}$$

$5) \int (\sin 9x+\frac{4}{5x-2}) dx =-\frac{1}{9} \cos 9x +\frac{4}{5} \ln \left|5x-2\right| + C$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ملاحظة: يمكن التحقق من صحة الحل بإعادة اشتقاق ناتج التكامل ،

                ومقارنة ناتج الاشتقاق بالاقتران المكامَل.

 

فمثلًا يمكن التحقق من صحة الحل بالمثال السابق للفرع (1) باتباع الخطوات الآتية:

1) الحل السابق: $-\frac{1}{64}{(9-8x)}^8+C$

2) الاشتقاق للحل:

  $$\begin{gathered} -\frac{1}{64}\times (-8){\times 8\times (9-8x)}^7+0 \\ =-\frac{1}{64}\times -64 {\times (9-8x)}^7 \\ =\frac{-64}{-64}{\times (9-8x)}^7 \\ ={(9-8x)}^7 \end{gathered}$$

 

3) المقارنة:

ناتج الاشتقاق: ${(9-8x)}^7$

الاقتران المكامَل: ${(9-8x)}^7$

بما أن ناتج الاشتقاق = الاقتران المكامَل فإن الحل صحيح.

---

رابعًا: الشرط الأولي:

تعلمت في درس سابق أن الشرط الأولي:

1) هو نقطة تحقق الاقتران الأصلي.

2) يمكن بتعويضه إيجاد ثابت التكامل $C$.

3) يمكن باستخدامه تحديد الاقتران الأصلي الوحيد الذي يحقق شرط المسألة.

4) يمكن استعماله لتحديد اقترانات تنمذج مواقف علمية وحياتية.

 

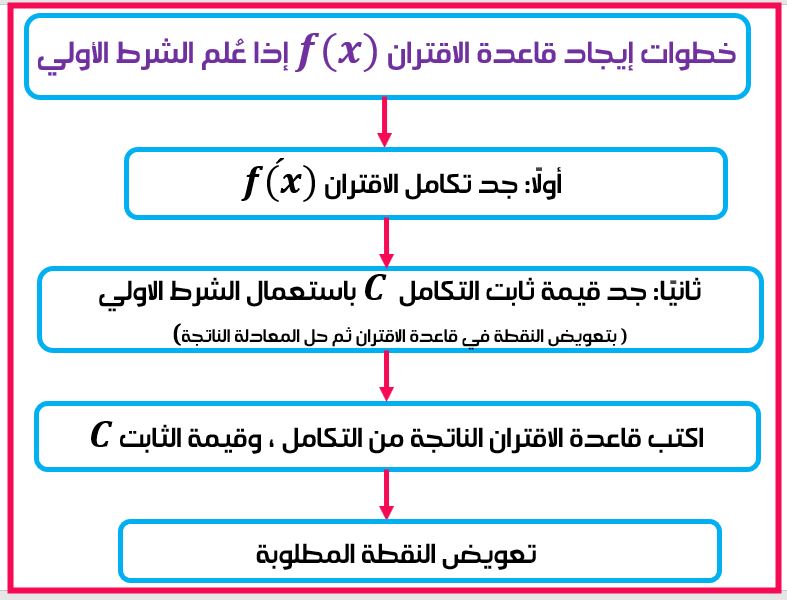
ويمكن تذكر خطوات استخدام الشرط الأولي لإيجاد نقطة معينة من خلال المخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال(4): يمثل الاقتران: $C َ \left(x\right) = 20 e^{0.5x}$ التكلفة الحدية (بالدينار)

               لكل حاسب لوحي تنتجه إحدى الشركات، حيث $x$ عدد الحواسيب

              المنتجة و $C\left(x\right)$ تكلفة إنتاج $x$ حاسب لوحي بالدينار.

              ما تكلفة إنتاج 12 حاسب لوحي علمًا بأن تكلفة إنتاج حاسب لوحي

                                واحد هي 120 JD

 

الحل:

الخطوة الأولى: جد تكامل الاقتران:$C َ \left(x\right)$

                          $$\begin{gathered} C \left(x\right) =\int 20 e^{0.5 x }dx \\ =\frac{20}{0.5} e^{0.5x}+C \\ = 40 e^{0.5x}+C \end{gathered}$$

                      

الخطوة الثانية: جد ثابت التكامل C:

 بتعويض النقطة $C\left(1\right) = 120$ ، $x=1$

                    $$\begin{gathered} C\left(1\right)= 40 e^{0.5\left(1\right)}+C \\ 120 = 40 \times 1.65 +C \end{gathered}$$

                                $$\begin{gathered} 120 = 66 +C \\ \to C=120-66 \\ \therefore C=54 \end{gathered}$$

إذن اقتران التكلفة هو: $C\left(x\right) = 40 e^{0.5x}+54$

 

الخطوة الثالثة: جد $C\left(12\right)$ بتعويض $x=12$

    $$\begin{gathered} C\left(12\right) = 40 e^{0.5\left(12\right)}+54 \\ =40 e^6 +54 \\ \approx 16191.15 \end{gathered}$$

إذن تكلفة إنتاج 12 حاسب لوحي تقريبًا هي 16191 JD

---

خامسًا: إيجاد تكامل اقترانات في صورة $k \frac{f َ\left(x\right)}{f\left(x\right)}$:

يمكن إيجاد تكامل الاقترانات التي يكون بسطها أحد مضاعفات مشتقة مقامها.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال(5): جد كلًّا من التكاملات الآتية:

                            $$\begin{gathered} 1) \int \frac{6x^2}{x^3+10}dx \\ 2) \int \frac{7x}{2x^2+3}dx \\ 3) \int \frac{3 \sin x}{2+\cos x}dx \end{gathered}$$

الحل:

$1) \int \frac{6x^2}{x^3+10}dx$
$\frac{d}{dx}\left(x^3+10\right)= 3x^2$	مشتقة المقام
بما أن البسط $\left(6x^2\right)$ أحد مضاعفات المقام فإننا نعيد كتابته:
$\int \frac{6x^2}{x^3+10}dx=2\int \frac{3x^2}{x^3+10}dx$	بإعادة كتابة الاقتران في صورة: $k \frac{f َ\left(x\right)}{f\left(x\right)}$
$= 2 \ln \left|x^3+10\right|+C$	تكامل $\frac{f َ\left(x\right)}{f\left(x\right)}$

 

 

 

 

 

 

 

 

 

 

$2) \int \frac{7x}{2x^2+3}dx$
$\frac{d}{dx}(2x^2+3)= 4x$	مشتقة المقام
بما أن البسط $\left(7x\right)$ومشتقة المقام $\left(4x\right)$ فإننا نضرب البسط والمقام بالعدد 4  لنعيد كتابته:
$$\begin{gathered} \int \frac{7x}{2x^2+3}dx = \frac{1}{4}\int \frac{4\times 7x}{2x^2+3}dx \\ =\frac{7}{4}\int \frac{4x}{2x^2+3}dx \end{gathered}$$	بالضرب بــ(4) والقسمة على (4)لإعادة كتابة الاقتران في صورة:$k \frac{f َ\left(x\right)}{f\left(x\right)}$
$=\frac{7}{4}\ln \left|2x^2+3\right|+C$	تكامل $\frac{f َ\left(x\right)}{f\left(x\right)}$

          

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

$3) \int \frac{3 \sin x}{2+\cos x}dx$
$\frac{d}{dx}(2+\cos x)=- \sin x$	مشتقة المقام
بما أن البسط $\left(3 \sin x\right)$ ومشتقة المقام $\left(- \sin x\right)$ فإنه يمكن كتابة البسط على الصورة الآتية:
$\int \frac{3 \sin x}{2+\cos x}dx=-3\int \frac{- \sin x}{2+\cos x}dx$	بإعادة كتابة الاقتران في صورة:$k \frac{f َ\left(x\right)}{f\left(x\right)}$
$= -3 \ln \left|2+ \cos x\right| + C$	تكامل $\frac{f َ\left(x\right)}{f\left(x\right)}$

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

سادسًا: التكاملات المحدودة لاقترانات خاصة:

يمكن إيجاد التكامل المحدود لجميع الاقترانات الخاصة التي تعلمتها خلال هذا الدرس بالخطوات الآتية: 

1) جد تكامل الاقترانات الخاصة .

2) عوض الحد الأعلى والحد الأدنى بالتكامل.

3) جد الفرق بينهما.

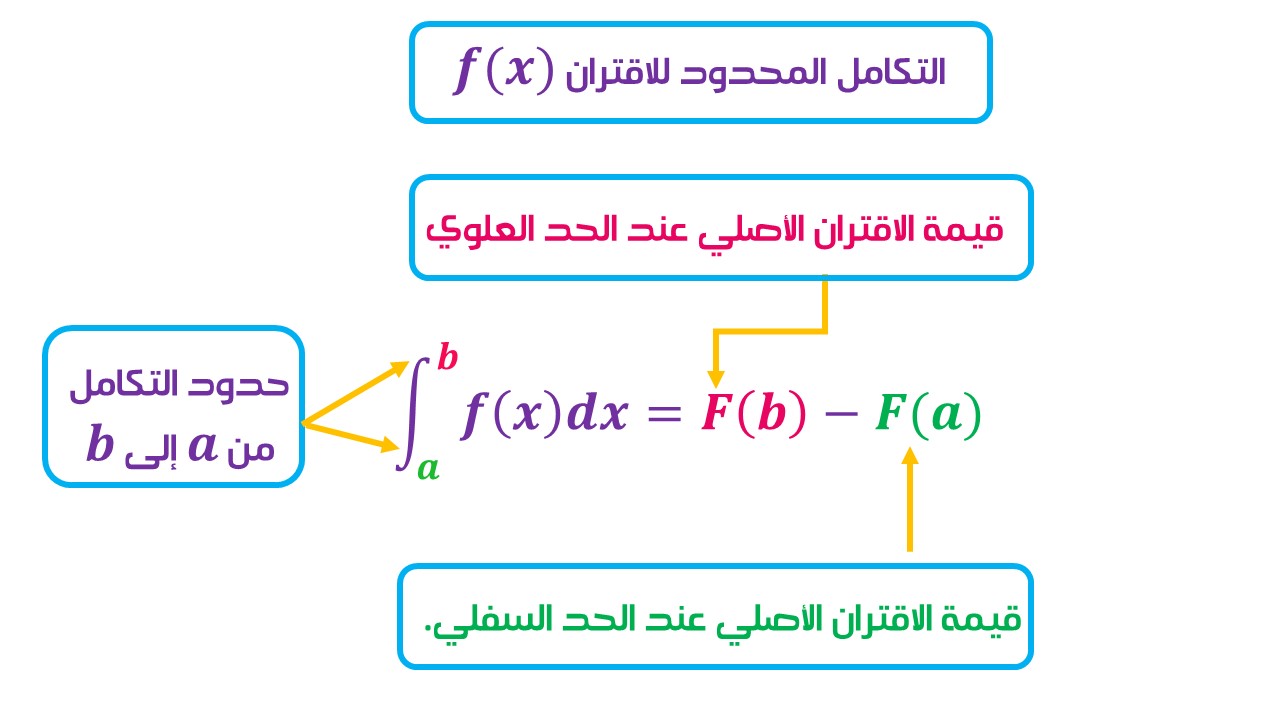
ويمكن تذكر قاعدة التكامل المحدود من خلال المخطط الآتي:

 

 

 

 

 

 

 

 

 

 

 

 

 

مثال(6): جد كلًّا من التكاملات الآتية:

                          $$\begin{gathered} 1) {\int }_0^{3}8 e^{12-4x} dx \\ 2) {\int }_2^3\frac{15}{3x-5} dx \end{gathered}$$

 

الحل:

$1) {\int }_0^{3}8 e^{12-4x} dx$
$$\begin{gathered} {\int }_0^{3}8 e^{12-4x} dx = \left(-\frac{8}{4}{e}^{12-4x}\right) \overline{)\begin{array}{c}3\\ \\ 0\end{array}} \\ =\left(-2 e^{12-4x}\right) \overline{)\begin{array}{c}3\\ \\ 0\end{array}} \end{gathered}$$	تكامل الاقتران الأسي الطبيعي المضروب في ثابت
$=-2 \left[\left(e^{12-4\left(3\right)}\right)-\left(e^{12-4\left(0\right)}\right)\right]$	بالتعويض
$$\begin{gathered} =-2\left(e^0 - e^{12}\right) \\ =-2\left(-e^{12}\right) \\ =2 e^{12} \end{gathered}$$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

$2) {\int }_2^3\frac{15}{3x-5} dx$
$$\begin{gathered} {\int }_2^3\frac{15}{3x-5} dx=15 {\int }_2^3\int \frac{1}{3x-5}dx \\ = \left[15 \left(\frac{1}{3}\right) \ln \left|3x-5\right|\right]\overline{)\begin{array}{c}3\\ 2\end{array}} \\ = \left[5 \ln \left|3x-5\right|\right] \overline{)\begin{array}{c}3\\ 2\end{array}} \end{gathered}$$	تكامل $\frac{1}{ax+b}$
$=5\left[\left(\ln \left|3\left(3\right)-5\right|\right)-\left(\ln \left|3\left(2\right)-5\right|\right)\right]$	بالتعويض
$$\begin{gathered} =5 \left[\ln 4 - \ln 1\right] \\ =5 \ln 4 \end{gathered}$$	بالتبسيط حيث: $ln 1 = 0$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

انتهى الدرس