رياضيات9 فصل أول

حلُّ المُعادلاتِ التربيعيَّةِ بالتحليلِ(2)

Solving Quadratic Equations by Factoring (2)

فكرةُ الدرسِ :  تحليلُ ثلاثِيِّ الحدودِ على الصورةِ $a{x}^2+bx+c$.  

                        حلُّ المُعادلاتِ التربيعيَّةِ على الصورةِ $a{x}^2+bx+c=0$ بالتحليلِ.

أولًا : تحليلُ ثلاثِيِّ الحدودِ $a{x}^2+bx+c$

تعلَّمتُ سابقًا كيف أُحلِّل ثلاثيَّ الحدود x² + bx + c ، الذي معامل x² فيهِ يُساوي 1، ويمكن أيضًا تحليل بعض ثُلاثيات الحدود التي على الصورة

ax² + bx + c ؛ حيثُ a ≠ 1 و a ≠ 0 بطريقة مُشابهة.

مفهومٌ أساسيٌّ (تحليلُ ثلاثيَّةِ الحدودِ $a{x}^2+bx+c$)

لتحليل ثلاثِيِّ الحدود $a{x}^2+bx+c$ ، أَجِدُ عددين صحيحين m وَ n حاصلُ ضربهما يُساوي ( ac ) ، ومجموعُهُما يُساوي b، ثمَّ أكتبُ $a{x}^2+bx+c$ على الصورةِ $a{x}^2+mx+nx+c$ ، ثمَّ أُحَلِّل بتجميع الحدود.

•• إذا كانتْ إشارةُ c موجبةً في ثلاثِيِّ الحدودِ ax² + bx + c ، حيث a > 0 ، فإنَّ لكلٍّ مِنْ m وَ n الإشارةَ نفسَها، ويعتمدُ تحديدُ إشارتَيْ mوَ n

(موجبةٌ أو سالبةٌ) على إشارةِ b، فإذا كانتْ b موجبةً فإنَّ إشارةَ كلٍّ منهُما موجبةٌ، وإذا كانتْ إشارةُ b سالبةً فإنَّ إشارةَ كلٍّ منهُما سالبةٌ.

 

مثال 1 : (عندما تكون a > 0  ، $c$ موجبة ، $b$موجبة )

أُحَلِّلُ $2x^2 +13x +15$

الحل  : 

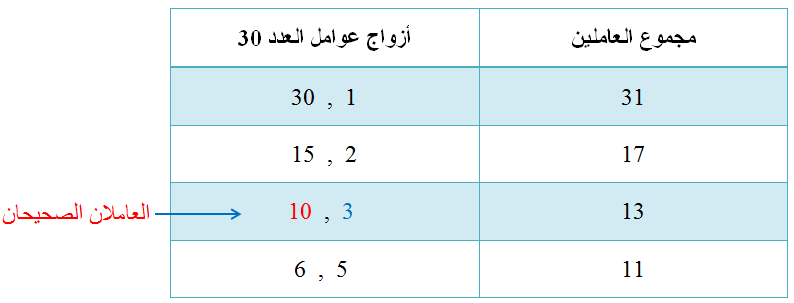
بما أنَّ a = 2 , b = 13 , c = 15  ، فأبحثُ عنْ عددَيْنِ حاصلُ ضربِهِما 30 = 15 × 2 ومجموعُهُما 13 . وبما أنَّ إشارةَ كلٍّ مِنْ c وَ b موجبةٌ، فَأُنْشِئُ جدولًا

أُنَظِّمُ فيهِ أزواجَ عواملِ العددِ 30 الموجبةَ، ثمَّ أُحَدِّدُ العامِلَيْنِ اللذَيْنِ مجموعُهُما 13 .

 

$2x^2 +13x +15 = 2x^2+mx+nx +15$	بكتابةِ القاعدةِ
$= 2x^2+10x+3x +15$	بتعويض m = 10 ,  n = 3
$= (2x^2+10x)+(3x+15)$	بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ
$= 2x (x+5)+3(x+5)$	بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر
$=(x+5)(2x+3)$	بإخراجِ (x + 5) عاملًا مُشترَكًا

أتحقَّقُ من صِحَّة التحليل بضرب العامِلين : 

$(x+5)(2x+3) = 2x^2+3x+10x+15$	خاصيَّة التوزيع
$= 2x^2 +13x +15 ✔$	بالتبسيط

 

 

---

 مثال 2 : (عندما تكون a > 0  ،  $c$ موجبة ، $b$سالبة )  

أُحَلِّل $8x^2 -17x +2$

الحل  : 

بما أنَّ a = 8 , b = -17 , c = 2  ، فأبحثُ عنْ عددَيْنِ حاصلُ ضربِهِما 16 = 8 × 2 ومجموعُهُما  17- . بما أنَّ b سالبةٌ وَ c موجبةٌ، فَأُنْشِئُ جدولً أُنَظِّمُ

فيهِ العامِلَيْنِ اللذَيْنِ مجموعُهُما 17 -  

 

 

$8x^2 -17x +2 = 8x^2+mx+nx+2$	بكتابةِ القاعدةِ
$= 8x^2-16x-x+2$	بتعويض m = -16 ,  n = -1
$= (8x^2-16x)+(-x+2)$	بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ
$= 8x (x-2)+(-1)(x-2)$	بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر
$= (x-2) (8x -1)$	بإخراجِ (x - 2) عاملًا مُشترَكًا

أتحقَّقُ من صِحَّة التحليل بضرب العامِلين : 

$(x-2)(8x-1) = 8x^2-x-16x+2$	خاصيَّة التوزيع
$= 8x^2 - 17x + 2 ✔$	بالتبسيط

 

 

 

••  أتعلَّمُ : لتسهيلِ عمليَّةِ التحليلِ مِنَ الأفضلِ أنْ أجعلَ معاملَ x2 موجبًا.

•• إذا كانتْ c سالبةً في ثُلاثيِّ الحدودِ ax² + bx + c ، حيث a > 0 ، فإنَّ لِـ m وَ n إشارتَيْنِ مُختلِفَتَيْنِ.

 مثال 3 : (عندما تكون a > 0  ، $c$ سالبة)

أُحَلِّل $6x^2+x-2$

الحل  : 

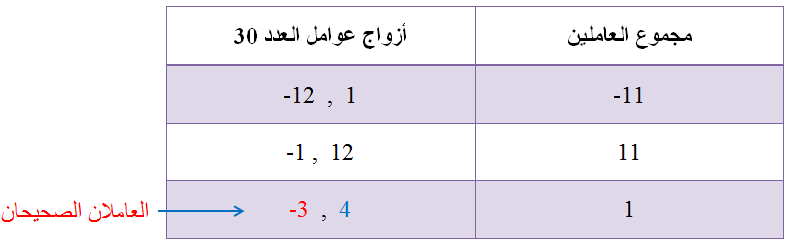
بما أنَّ a = 6 , b = 1 , c = - 2 ، فأجِدُ عددَيْنِ حاصلُ ضربِهِما 12- = 2- × 6  ومجموعُهُما 1  

بما أنَّ c سالبة ، فأُنشئ جدولًا أُنظّم فيه أزواج عوامل العدد (12 -) مختلفةَ الإشارةِ، ثمَّ أُحَدِّدُ العامِلَيْن اللذَيْن مجموعُهُما 1

$6x^2+x -2 = 6x^2+mx+nx-2$	بكتابةِ القاعدةِ
$= 6x^2+(-3)x+4x-2$	بتعويض m = -3 ,  n = 4
$= (6x^2-3x) +(4x-2)$	بتجميعِ الحدودِ ذاتِ العواملِ المُشترَكةِ
$= 3x (2x-1)+2(2x-1)$	بتحليل كلِّ تجميع بإخراج العامل المُشترك الأكبر
$= (2x-1)(3x+2)$	بالتبسيط

أتحقَّقُ من صِحَّة التحليل بضرب العامِلين : 

$(2x-1)(3x+2) = 6x^2+4x-3x-2$	خاصيَّة التوزيع
$= 6x^2+x-2 ✔$	بالتبسيط

---

ثانيًا : حلُّ المُعادلاتِ على الصورةِ ax² + bx + c = 0 بالتحليلِ

يمكنُ حلُّ المُعادلاتِ التربيعيَّةِ على الصورةِ ax² + bx + c = 0 بالتحليلِ أوَّلًا ، ثمَّ استخدام خاصيَّةِ الضَّربِ الصِّفريِّ.

مثال : 

أَحلُّ كُلًّ من المُعادلات الآتية: 

$\mathit{a}\mathbf{)} 5x^{2 }+ 21x +4 = 0$

$5x^2+21x+4=0$	المُعادلة المُعطاة
$(5x+1)(x+4)=0$	بالتحليل إلى العوامل
$5x+1=0 or x+4=0$	خاصيّة الضرب الصفريّ
$x=-\frac{1}{5} or x=-4$	بحلّ كلّ مُعادلة

---

$\mathit{b}\mathbf{)} 21x^2+ 6 = 45x$

$21x^2+6 = 45x$	المُعادلة المُعطاة
$21x^2-45x+6 = 0$	بطرح 45x من طرفي المعادلة
$7x^2-15x+2 = 0$	بقِسمة طَرفي المُعادلة على 3
$(7x - 1)(x - 2) = 0$	بالتحليل إلى العوامل
$7x-1 = 0 or x-2 = 0$	خاصيّة الضرب الصفريّ
$x=\frac{1}{7} or x =2$	بحلّ كلّ مُعادلة

•• أتذكَّرُ : أحرِص دائمًا على إخراج العامل المُشترَك الأكبر أوَّلًا قبل البَدء بعمليَّة التحليل.

• يمكنُ استعمالُ حلِّ المُعادلاتِ التربيعيَّةِ بالتحليلِ في كثيرٍ مِنَ التطبيقاتِ الحياتيَّةِ. 

مثال : 

مستطيل يزيد طوله على 3 أمثال عرضه بمقدار $5m$ ، إذا كانت مساحة المستطيل$68m^2$ ، فأجد أبعاده . 

الحل  : 

أفرض عرض المستطيل x  ، إذن طوله  3x + 5

مساحة المستطيل  = الطول $\times$ العرض  ، إذن :  $x(3x + 5) = 68$

أكتب المعادلة بالصورة القياسية وأحللها 

$3x^2+5x-68=0$

$(3x+17)(x-4)=0$

$3x+17=0 or x-4=0$

$x=-\frac{17}{3} or x=4$

تُهمل الإجابة السالبة ؛ لأنها مسافة ، إذن x = 4  

إذن : عرض المستطيل$4m$ ، وطوله $17m$