دارات التيار الكهربائي المتردّد
|
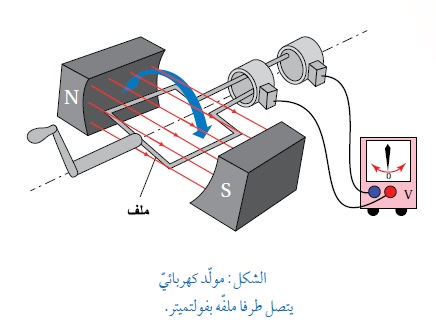
التيار الكهربائي المتردد: هو تيار كهربائي يتغير مقداره واتجاهه بشكل دروي، يبدأ من الصفر ويزداد إلى الحد الأقصى، وينخفض إلى الصفر، وينعكس، ويصل إلى الحد الأقصى في الاتجاه المعاكس، ويعود مجدداً إلى القيمة الأصلية. ويكرر هذه الدورة 60/50 مرة كل ثانية (بمعنى آخر بتردد50Hz أو 60Hz). كما ألاحظ من الشكل المتحرك المجاور أن التيار يعكس اتجاهه كل نصف دورة. |
|
|
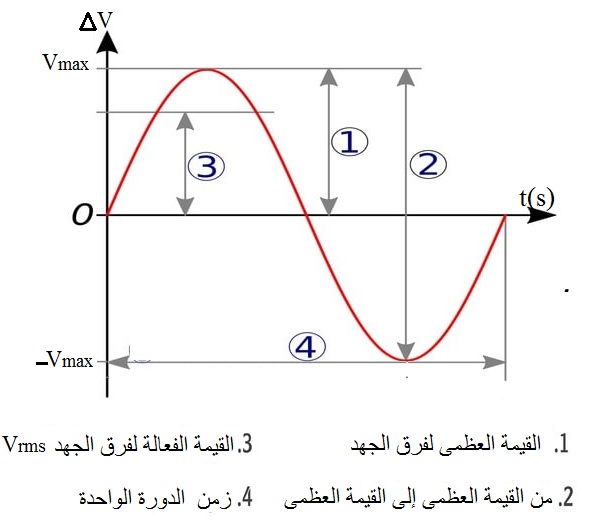
فرق الجهد الكهربائي المتردّد Alternating Potential Difference في المولد الكهربائي وأثناء دوران الملف في المجال المغناطيسي تتغير الزاوية بين اتجاه المجال المغناطيسي والعمود المقام على سطح الملف، ما يجعل التدفق عبر سطح الملف يتغير باستمرار. وبتطبيق قانون فارادي في الحثّ على الملفّ في أثناء دورانه، أجد أنّ القوّة الدافعة الكهربائيّة الحثّية تتغيّر وَفْقَ علاقة جيبيّة، لذا، فإنّ فرق الجهد بين طرفي الملف يتغيّر مع الزمن، ويُسمّى فرق جهد متردّد يُعبَّر عنه بالعلاقة:
حيث: Vmax: القيمة العظمى لفرق الجهد. : التردد الزاوي يقاس بوحدة rad/s وعندما يدور الملف بتردد ( ) وبزمن( T ):
مثال 1: يُزوّدنا مولّد كهربائي بفرق جهد متردّد، قيمته العظمى تساوي ( 310V )، وتردّده ( 50Hz ). أكتب معادلة فرق الجهد المتردّد، ثمّ أجد مقدار فرق الجهد عند: . معادلة فرق الجهد: لكتابة معادلة فرق الجهد، أحتاج مقدار كل من التردد القيمة العظمى لفرق الجهد التردد الزاوي:
لذلك تكون معالة فرق الجهد:
مقدار فرق الجهد عند اللحظة:
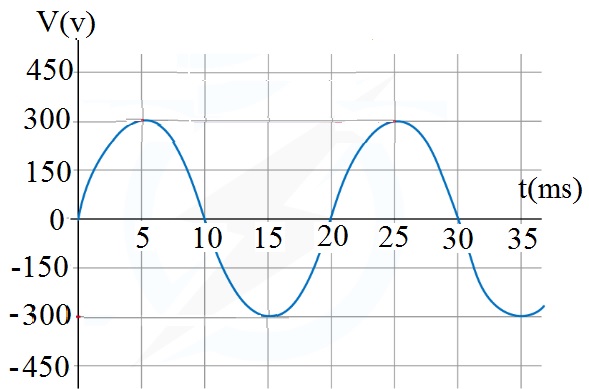
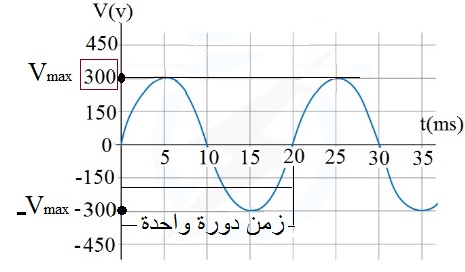
مثال 2: يمثل الرسم البياني المجاور منحنى فرق الجهد الكهربائي المتردد، الناشئ عن دوران ملف مولد كهربائي حول محور متعامد مع مجال مغناطيسي منتظم، إعتماداً على البيانات الواردة في الرسم أجب عما يأتي: أ- ما القيمة العظمى لفرق الجهد المتردد؟ ب- ما الزمن الدوري لدوران الملف. ج- أجد تردد فرق الجهد الناتج عن المولد. د- أجد السرعة الزاوية لدوران الملف. هـ-أكتب المعادلة الجيبية لفرق الجهد الناتج عن المولد . الحل: أ- القيمة العظمى لفرق الجهد المتردد من الشكل: ب_ الزمن الدوري لدوران الملف هو زمن دورة واحدة، ومن الشكل: ج- تردد فرق الجهد:
د- السرعة الزاوية = التردد الزاوي
هـ- معادلة فرق الجهد ( معادلة جيبية)
|
|
|
المقارنة بين التيار الكهربائي المتردّد والتيار الكهربائي المستمرّ (المباشر) يزوّدنا المولّد الكهربائي بتيار متردّد ( Alternating current (AC كما في الشكل المتحرك التالي: وتزوّدنا البطاريات بمختلف أنواعها بتيار كهربائي مستمرّ ( Direct current (DC . كما في الشكل المنحرك التالي: تزوّد شركات الكهرباء المنازل والمباني بالطاقة الكهربائية على شكل تيار متردّد، ونحصل على التيار المتردّد من المقابس الكهربائيّة في المنازل مثلاً، ولأنّ أكثر الأجهزة الكهربائية مثل الحاسوب والتلفاز والهاتف يعمل بالتيار المستمر، فإنّها تكون مزوّدة بدارة إلكترونيّة لتحويل التيار المتردّد إلى تيار مستمر (ستتعرّفها في الدرس اللاحق)، في حين أنّ هناك أجهزة أخرى تعمل بالتيار المتردّد مباشرة، كالغسالة والمدفأة. ويبين الجدول التالي المقارنة بين التيار المتردد والتيار المستمر:
|
|
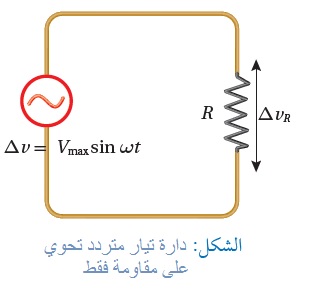
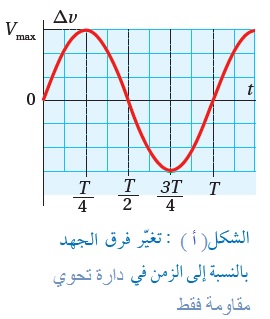
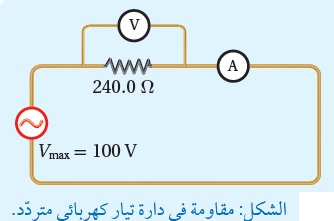
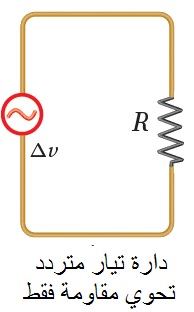
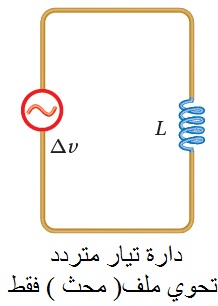
دارات التيار الكهربائيّ المتردّد البسيطة Simple AC Circuits وهي دارة تيار متردّد تحوي على مصدر فرق جهد متردّد ومقاومة ( Resistor (R كما في الشكل المقابل، الشكل ( أ ) المقابل يمثل العلاقة البيانية بين فرق الجهد المتردد والزمن في الدارة. وبتطبيق قاعدة كيرشوف الثانية على الدارة البسيطة المغلقة نحصل على:
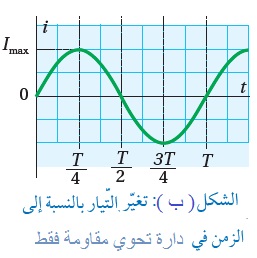
ومن هذه العلاقة يمكن إيجاد قيمة التيار المتردد عند أي لحظة زمنية. الشكل (ب ) يمثل العلاقة البيانية بين التيار التردد والزمن في دارة تحوي مصدر جهد متردد ومقاومة فقط. |
|
|
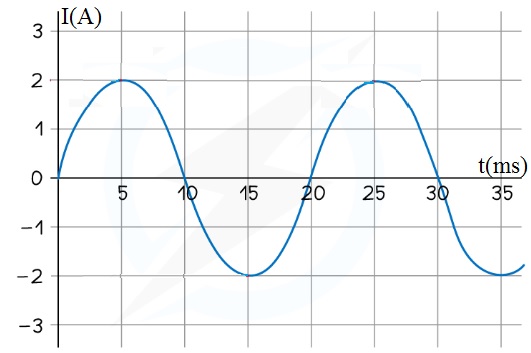
مثال3: دارة تحوي مقاومة فقط مقدارها ( )، متصلة مع مصدر تيار متردد، والرسم البياني المقابل يمثل العلاقة بين التيار والزمن. اعتماداً على البيانات على الشكل، أحسب ما يلي: أ- التيار عند اللحظة الزمنية( t=2.5ms). ب- القيمة العظمى لفرق الجهد ( ). الحل: أ- لأيجاد التيار عند اللحظة ( t=0.25s )، أجد كل من القيمة العظمى للتيار( ) والتردد الزاوي ( ): من الشكل: ، ومقدار التردد الزاوي:
معادلة التيار المتردد عند أي لحظة زمنية تعطى بالعلاقة التالية:
ومنها أجد التيار عند اللحظة (2.5ms ):
ب- القيمة العظمى لفرق الجهد:
|
 |
|
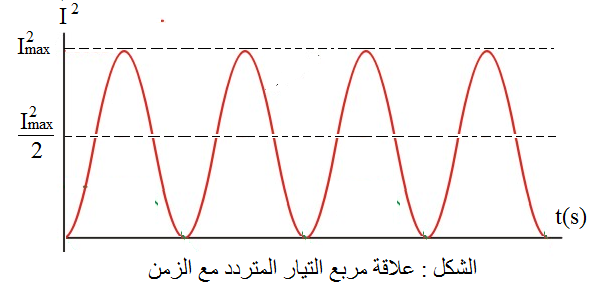
القدرة المستهلكة في المقاومة Power Dissipated in the Resistor ألاحظ من الشكل( أ ) التالي أن التيار المتردد يتغير بين القيمة العظمى الموجبة والقيمة العظمى السالبة. لذلك يكون المتوسط الحسابي للتيار يساوي صفر. إذاً كيف يتم قياس التيار باستخدام الأميتر لحساب القدرة المستهلكة باستخدام العلاقة التالية:
لذلك نحتاج إلى قيمة ثابتة للتيار حتى يقيسها الأميتر ومن ثم حساب القدرة، وهذه القيمة الثابتة تسمي الجذر التربيعى للقيم المتوسطة لمربع التيار، ويرمز لها ( ) والشكل التالي يمثل الرسم البياني لمربع التيار مع الزمن: نلاحظ من الشكل أن القيمة المتوسطة لمربع التيار تساوي: : بالتالي يكون الجذر التربيعي للقيمة المتوسطة لمربع التيار تعطى كما يلي
أيْ إنّ القدرة المتوسطة المستهلَكة في مقاومة عند سريان تيار متردّد فيها،هي القدرة المستهلكة نفسها الناتجة عن سريان تيار ثابت في المقاومة نفسها و وقيمته: ( ). وبذلك فإنّ، القدرة المتوسطة المستهلكة في المقاومة عند سريان تيار متردّد فيها تُحسب باستخدام العلاقة الآتية:
وبالمثل، يمكن حساب قيمة ثابتة لفرق الجهد المتردّد يُرمز إليها بـ ( ) ويُعبَّر عنها بالعلاقة:
إن استخدام القيمتين ( ) و ( ) يسهّل علينا دراسة دارات التيارات المتردّدة، فأجهزة الأميتر والفولتميتر تستخدم لقياس لقياس هذه القيم على الترتيب، , وهذه تسمى القيم الفعالة لكل من الجهد المتردد والتيار المتردد. ويُستخدم جهاز راسم الذبذبات للحصول على منحنى فرق الجهد المتردّد-الزمن . أفكر: كيف يمكن حساب القدرة الكهربائيّة التي تستهلكها مقاومة كهربائيّة عندما تعمل بتيار متردّد، ومقارنتها بقدرتها في حالة عملها بالتيار المستمر؟ الجواب:القدرة الكهربائية المستهلكة في مقاومة عندما يسري فيها تيار متردد تساوي حاصل ضرب مربع القيمة الفعالة للتيار المتردد في مقدار المقاومة، أما عندما يسري فيها تيار مستمر، فإن القدرة تساوي حاصل ضرب مربع التيار المستمر في مقدار المقاومة. مثال4: جهاز كهربائيّ مقاومته ( 65 Ω )، وُصِل بمصدر فرق جهد متردّد، إذا علمت أنّ القيمة العظمى لفرق الجهد المتردّد بين طرفيه ( 325V )، وتردّده ( 60Hz )، أُحدّد: الحل: أ- الزمن الدوري: ب- القيمة العظمى للتيار: ج- الاقتران للتيار المتردّد بدلالة الزمن (t ): أجد التردد الزاوي:
مثال 5: القيمة العظمى لمصدر فرق الجهد المتردّد في دارة كهربائيّة ( 56V )، والقيمة العظمى للتيار المتردّد ( 2.8A ). أحسب: أ- القيمتين الفعّالتين ( Vrms و Irms ) للجهد والتيار في الدارة، ب - المقدار المتوقّع لمقاومة الدارة؟ الحل: أ- القيمة الفعالة للجهد:
القيمة الفعالة للتيار:
ب- المقاومة:
أتحقّق: ما القيمة الفعالة لفرق الجهد التي نحصل عليها من المقابس الجدارية في الأردن، علمًا أن القيمة العظمى لفرق الجهد 324V ؟ الحل: القيمة الفعالة لفرق الجهد:
مثال 6: مدفأة كهربائيّة مقاومتها ( 40Ω ) تعمل على فرق جهد متردّد بوحدة الفولت مُعبَّر عنه بالعلاقة: ( 310sin ωt )، حيث(t) بوحدة الثانية، أحسب: الحل: أ. القيمة الفعالة للتيار:
ب. القدرة الكهربائية:
|
|
المعاوقة:
نعلم أن المقاومة الكهربائية Resistance ( ) هي خاصية المادة
في مقاومة تدفق التيار،ناتجة عن تصادم الإلكترونات مع بعضها ومع
أنوية الذرات في المادة الناقلة للتيار المستمر أو التيار المتردد، ومقدار
المقاومة لا يعتمد على التردد الزاوي( )للتيار المتردد .
اما مصطلح المعاوقة Reactance هو خاصية المادة في مقاومة
التغير في التيار ( زيادة أو نقصان). لاحظ اننا نتحدث هنا على مقاومة
التغير في التيار وهذا يعني أننا نتعامل الآن مع تيار متردد.وتكون المعاوقة
بسبب انتقال التيار المتردد في الدارة سواء كان في ملف( محث ) أو في
مواسعة ( )، أي أن هناك:
1-معاوقة محثية رمزها ( ) تتناسب طردياً مع التردد للتيار()
حسب العلاقة التالية:
2- معاوقة مواسعية ( )تناسب عكسياً مع
التردد للتيار المتردد ( ) حسب العلاقة التالية:
3- في دارة المقاومة نعبّر عن القيمة العظمى للتيار
بالعلاقة:
والقيمة الفعالة بالعلاقة:
| أفكر: أقارن المجال المغناطيسي الذي يولّده مرور تيار متردّد في محثّ بالمجال الذي يولّده مرور تيار مستمر فيه من حيث الاتجاه. |
الجواب: يولد التيار المتردد المار في محث مجال مغناطيسي متغير المقدار والاتجاه على شكل اقتران جيبي. بينما يولد التيار المستمر المار في محث مجال مغناطيسي ثابت المقدار والاتجاه. |
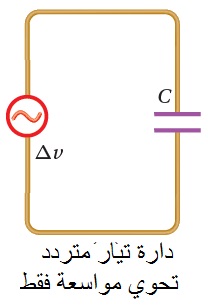
في حالة المحث والمواسع تُستخدام المعاوقة بدلاً من
المقاومة، على نحو ما هو موضح في الجدول التالي:
|
عناصر الدارة
|
 |
 |
 |
| المقاومة/ المعاوقة | |||
| وحدةقياس المقاومة/ المعاوقة | أوم() | أوم ( ) | أوم ( ) |
|
|
|||
|
|
العوامل التي تعتمد عليها كل من:
أ. المعاوقة المحثية: 1- مقدار المحاثة. 2-التردد لمصدر الجهد
( العلاقة طردية مع كل من العاملين)
ب.المعاوقة المواسعية: 1- مقدار المحاثة. 2-التردد لمصدر الجهد
( العلاقة عكسية مع كل من العاملين)
أفكر: ما مقدار معاوقة كلٍّ من المحث والمواسع عندما يكون
تردّد التيار الكهربائي صفراً، وعندما يكون تردّده كبير ا جداً؟
الجواب: - المعاوقة المحثية تتناسب طردياً مع تردد التيار ، فتكون
المعاوقة الحثيىة صفر عند التردد صفر، وكبيرة جداً عند
التردد الكبير جداً.
- المعاوقة المواسعية تتناسب عكسياً مع تردد التيار ، فتكون
المعاوقة المواسعية كبيرة جداً ( في الانهاية) عند التردد صفر،
وصغيرة جداً عند التردد الكبير جداً.
مثال 6: ملف محاثته 20mH في دارة القيمة الفعالة للجهد المتردد
فيها 150V، وتردد مصدر الجهد 50Hz. أحسب ما يلي:
أ. المعاوقة المواسعية.
ب. القيمة الفعالة للتيار الكهربائي.
ج. القيمة الفعالة للتيار إذا زاد التردد إلى 5kHz.
الحل: أ. المعاوقة المحثية:
ب. القيمة الفعالة للتيار:
ج. عند زيادة التردد تزداد المعاوقة المحثية، بالتالي تقل
القيمة الفعالة للتيار:
مثال 7: مواسع مواسعته في دارة القيمة الفعالة للتيار المتردد
0.6A، وتردد مصدر الجهد 50Hz. أحسب ما يلي:
أ. المعاوقة المواسعية.
ب. القيمة الفعالة لفرق الجهد المصدر.
الحل: أ. المعاوقة المواسعية:
ب. القيمة الفعالة لفرق الجهد:
|
أفكر:ما مقدار معاوقة كلٍّ من الجواب: معاوقة المحث = 0
وعندما يكون التردد كبير جداً، تكون المعاوقة المحثية كبيرة جداً. معاوقة المواسع في اللانهاية عند التردد صفر:
وتكون معاوقة المواسع صغيرة جداً عند التردد الكبير جداً. |
|
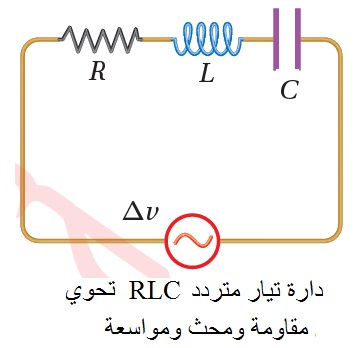
مقاومة ومحثّ ومواسع (RLC ) على التوالي في دارة تيار كهربائي متردّد.The RLC Series AC Circuit. حتوي هذه على العناصر الثلاثة، وهي مقاومة ( ) ومحثّ ( ) ومواسع ( ) موصولة جميعها على التوالي بمصدر فرق جهد متردّد، على نحو ما يبيّن ا لشكل المجاور. ويُرمز إلى المعاوقة الكليّة للدارة بالرمز ( )، ويُعبَّر عنها بدلالة معاوقات مكوّناتها الثلاثة بالعلاقة:
ويمكننا استخدام القيمة الفعّالة للتيار المتردد:
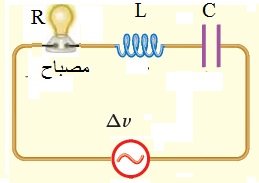
مثال 8: يمثل الشكل المجاور دارة تيار متردد تحوي محث ومصباح، ما يحدث لكل من إضاءة المصباح ومقاومته، إذا قل تردد مصدر الجهد الكهربائي مع بقاء سعة مصدر الجهد ثابتة؟ الحل: - إضاءة المصباح: إذا قل تردد مصدر الجهد فإن المعاوقة المحثية في الدارة تقل حسب العلاقة: لذلك تزداد قيمة التيار المار في الدارة، فتزداد قدرة المصباح،وتزداد إضاءته. - مقاومة المصباح: تبقى ثابتة، لأن المقاومة لا تعتمد على التردد. |
|
|
مثال 9: يبيّن الشكل المجاور دارة يتصل فيها مواسع ومصباح بمصدر فرق جهد متردّد، ماذا يحدث لإضاءة المصباح عند نقصان تردّد المصدر مع بقاء القيمة العظمى لفرق الجهد ثابتة؟ أفسّر إجابتي. الحل: وفقًا للعلاقة( ) ، فإنّ نقصان تردّد المصدر (في المقام) يؤدّي إلى زيادة معاوقة المواسع؛ فتزداد الممانعة التي يبديها المواسع لمرور التيار، ما يعني نقصان مقدار التيار المارّ في الدارة، ومن ثمّ نقصان القدرة المستهلكة في المصباح فتقل إضاءته. |
 |
|
مثال 10: دارة ( AC ) تحتوي على مصدر فرق جهد متردّد قيمته الفعّالة ( 150V ) وتردّده ( 60Hz )، يتّصل على التوالي بمقاومة ( 420Ω ) ومحثّ محاثّته ( 1.8H )، ومواسع مواسعته (7μF ). أجد كلًّ من: أ . المعاوقة المحثّية، والمعاوقة المواسعيّة، والمعاوقة الكليّة للدارة. ب. القيمة الفعّالة للتيار المتردّد. الحل: أ. المعاوقة المحثية:
المعاوقة المواسعية:
المعاوقة الكلية:
ب. القيمة الفعّالة للتيار المتردّد:
|
|
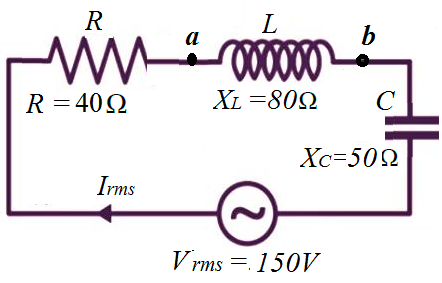
مثال 11: يمثل الشكل المقابل دارة RLC لمصدر جهد متردد، أعتماداً على القيم الواردة في الشكل،أحسب مايلي: أ. القدرة المتوسطة المستهلكة في المقاومة. ب. القيمة الفعالة لفرق الجهد بين النقطتين ( a ) و (b). ج. محاثة الملف ( L )،إذا كان تردد مصدر الجهد (50Hz ). د . القيمة العظمى لفرق جهد المصدر. الحل: أ. لإيجاد القدرة المستهلكة في المقاومة، نحتاج مقدار المعاوقة الكلية في الدارة للعناصر الثلاثة والقيمة الفعالة للتيار :
القيمة الفعالة للتيار:
القدرة المتوسطة في المقاومة:
ب. القيمة الفعالة لفرق الجهد بين النقطتين ( a ) و (b).:
ج. محاثة الملف ( L ):
د . القيمة العظمى لفرق جهد المصدر.
|
 |
|
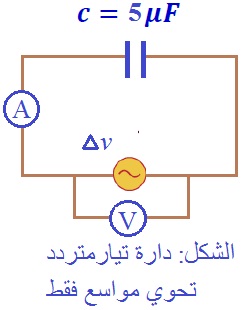
مثال 12: دائرة تيار متردد كما بالشكل تحوي مكثف فقط سعته 𝒄 = 5𝝁𝑭 متصل مع مصدر تيار متردد معادلة جهده = 80𝒔𝒊𝒏 100𝝅𝒕 ، أوجد ما يلي: أ. مقدار العظمى للتيار ؟ ب. قراءة كل من الفولتميتر والأميتر. الحل: أ. الدارة تحوي مواسع فقط: والتردد الزاوي: من اقتران فرق الجهد .
لأن الدارة لا تحوي مقاومة ولا محث( ملف ). بالتالي المعاوقة الكلية ( Z ):
ومنه تكون القيمة العظمى للتيار:
ب. قراءة كل من الفولتميتر والأميتر: يقيس كل من الفولتميتر والأميتر القيمة الفعالة لفرق الجهد() والتيار ( ) المترددين على الترتيب: قراءة الفولتميتر: قراءة الأميتر: |
 |
الرنين Resonance
نعلم الآن أن المعاوقة الكلية لدارة تيارمتردد تحوي
مقاومة ومحث ومواسع تعطى بالعلاقة التالية:
والقيمة الفعالة للتيار في الدارة:
ومن هذه العلاقة تكون القيمة الفعالة للتيار أكبر ما يمكن
عندما يكون المقام أقل ما يمكن، وهنا تكون الدارة في حالة
تسمى( الرنين Resonance)
تردد الرنين : والتردد الذي يحدث عنده الرنين في الدارة يسمى
التردد الطبيعي للدارة( ):
من هذه العلاقة نلاحظ أن التردّد الطبيعي للدارة يعتمد
على قيمة كلٍّ من مواسعة المواسع ومحاثّة المحثّ،
حيث يتناسب التردد الطبيعي للدارة عكسياً مع الجذر
التربيعي لكل من المحاثة ( ) والمواسعة ( C ).
أتحقّق: ماذا تمثّل حالة الرنين في دارة مقاومة ومحثّ
ومواسع؟
الجواب:يحدث الرنين في دارة مقاومة ومحث ومواسع
عند تردد معين لفرق الجهد، حيث تتساوى معاوقة المحث
مع معاوقة المواسع، وتكون معاوقة الدارة مساوية
للمقاومة فقط، والتيار الفعّال فيها له أكبر قيمة ممكنة.
|
أفكر: ما الشرط اللازم توافره كي ما يمكن عندما تكون المعاوقة المحاثية تساوي المعاوقة المواسعية: |
 |
|
مثال 13: دائرة تيار متردد، تحوي سعة المكثف 𝟏𝟔𝝁𝑭، ومحث محاثته ( 0.25H) , ومصباح كهربائي، عند أي تردد لمصدرالجهد يضيء المصباح بأكبر شدّة ممكنة؟ الحل: أكبر شدة ممكنة لإضاءة المصباح عن أكبر قيمة ممكنةللقيمة الفعالة لتيار، وعندها تكون الدارة في حالة رنين:
|
|
|
مثال 14: دارة تيار متردد تحوي محث ومواسعة، وكانت في حالة رنين عند مصدر الجهد المتردد ( )، ومقدار المعاوقة المحثية ( )، أجد مقدار كل مما يأتي: أ- التردد الطبيعي للدارة( ). ب- محاثة المحث (L ). ج. المواسعة للمواسع ( C ). الحل: أ- التردد الطبيعي للدارة: كون الدارة في حالة رنين،لذلك التردد الزاوي الوارد في المعادلة يمثل تردد الرنين:
ب- محاثة المحث (L ).
ج. المواسعة للمواسع ( C ). بما أن الدارة في حالة رنين، يكون:
بتربيع الطرفين:
|
|
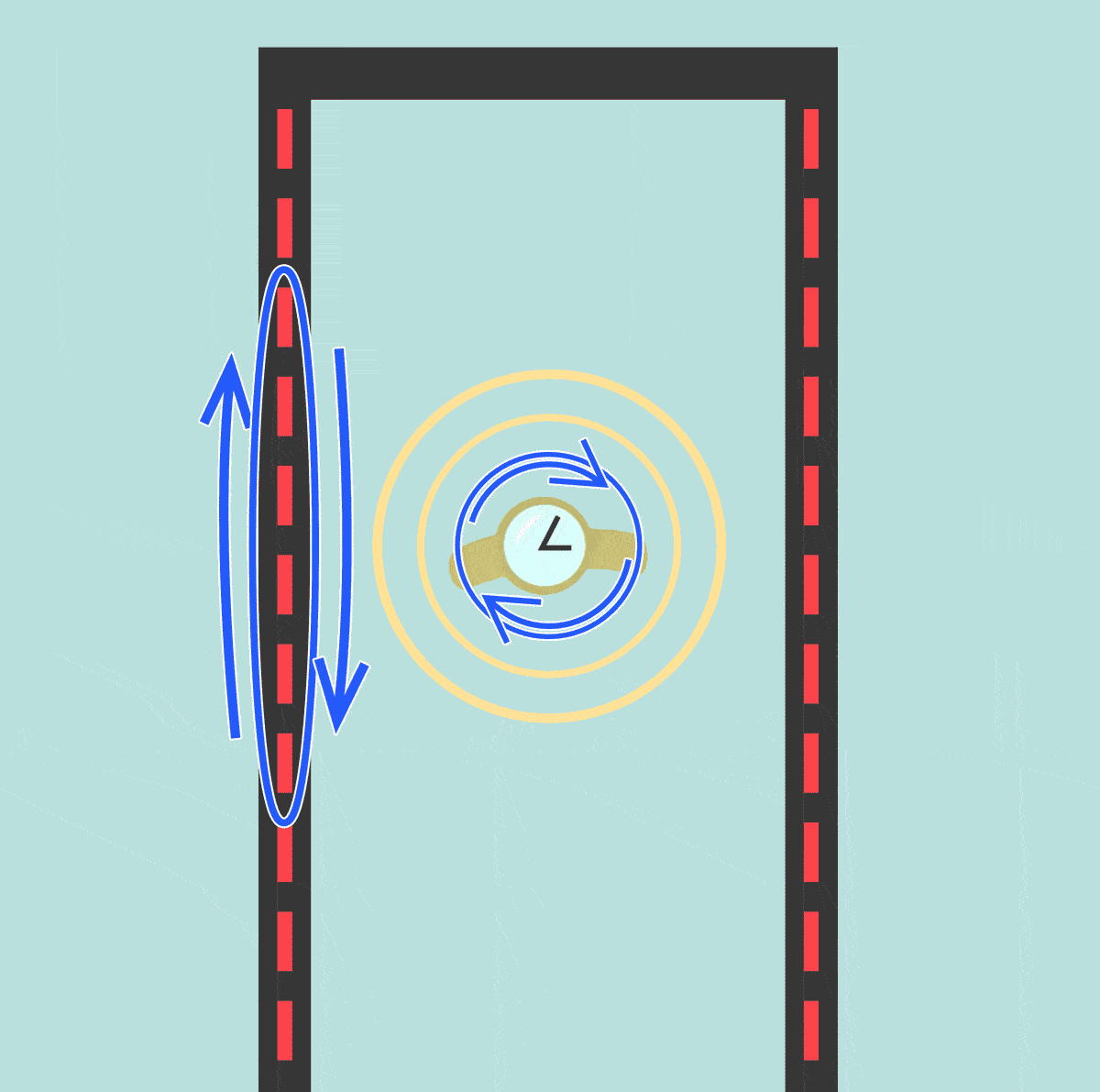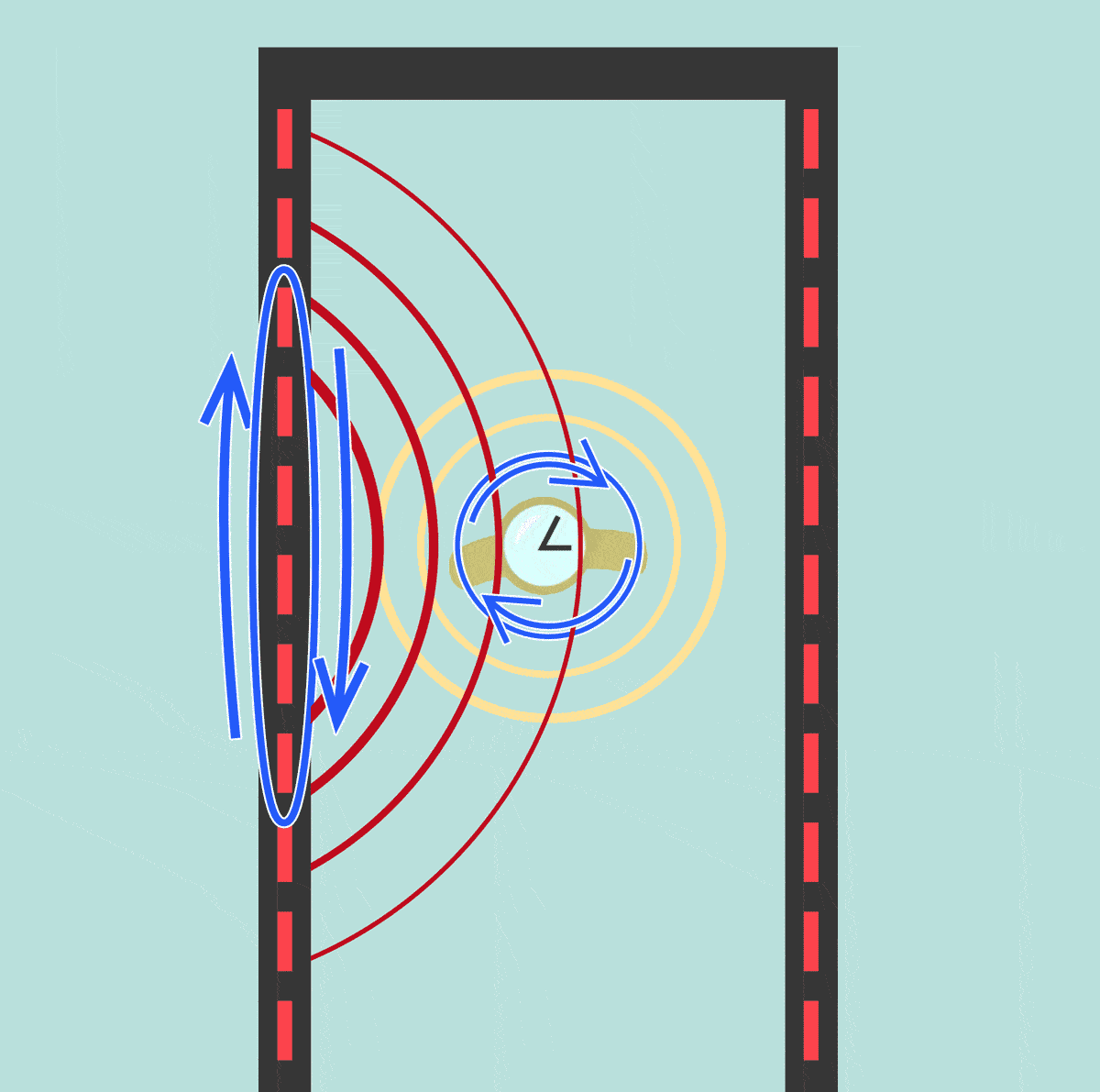
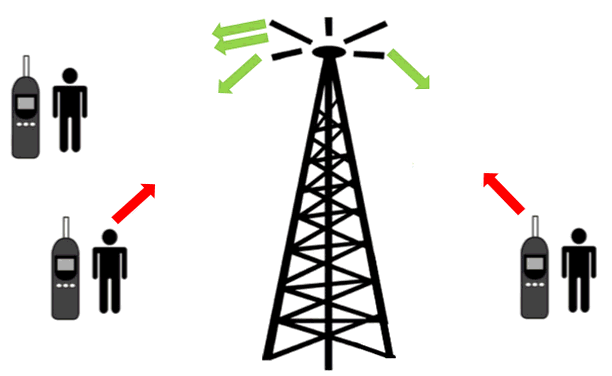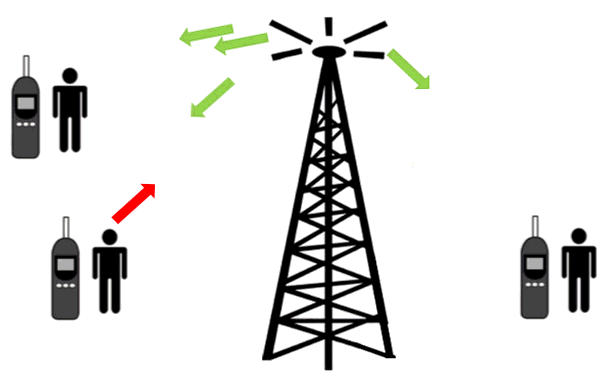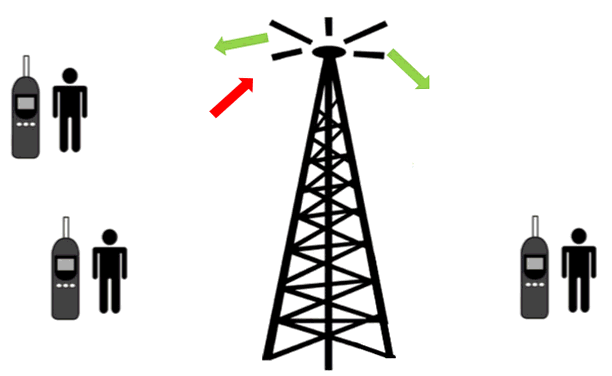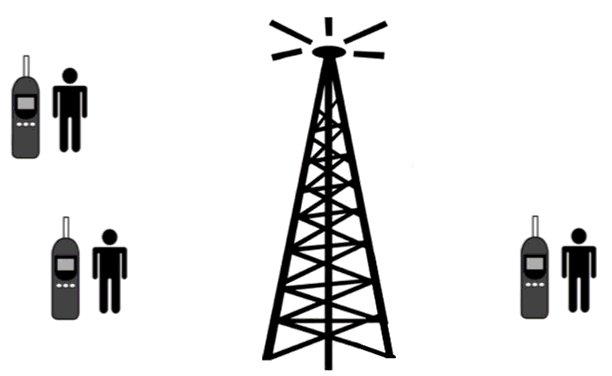
تطبيقات تكنولوجيّة تُستخدم في المطارات , وبعض المؤسسات بوابات للكشف عن الفلزّات، عندما يمرّ المسافر خلالها فإنّها تُصدر إشارة إذا كان المسافر يخفي أداة فلزّيّة. كما في المشهد المتحرك المقابل ويحتوي إطار البوابة على ملفٍّ من سلكٍ نحاسيّ يمثّل محثًّا في دارة ( RLC )، وتكون الدارة متّصلة بمصدر فرق جهدٍ متردّد، قد ضُبط تردُّده لإحداث حالة الرنين، وعند اقتراب جسم فلزّي من المحثّ، فإنّه يؤدّي إلى زيادة في محاثّته، فينعدم الرنين في الدارة، وينخفض التيار الفعّال فيها عن أكبر قيمة له، ثم تحوِّل دارة إلكترونيّة ذلك التغيير في التيار إلى إشارة تحذيريّةمسموعة وأخرى مرئيّة. 2-أجهزة المذياع والاتصال اللاسلكي: جميع أجهزة الاتصال اللاسكي تتكون من دارة أرسال ودارة استقبال، وأجهزة المذياع وأجهزة التلفاز وأجهزة الاتصال اللاسلكي، تُعدّ مثالاً مهمًّا على دارة الرنين، فمحطات الإذاعة والبث التلفزيوني(الإرسال) تبثّ برامجها على شكل موجات كهرمغناطيسية، بتردد محدّدة، وعندما يضبط أحدُنا مفتاح الموجة في المذياع والتلفاز على إذاعة أو قناة معينة، فإنّه يغيّر من مواسعة المواسع في دارة الرنين داخل المذياع أو التلفاز، ما يغيّر من تردد الرنين لدارة الاستقبال ليصبح مطابقًا لتردّد الموجات المرسلة، ثم تُمرّر هذه الموجات بعد تكبيرها إلى مكبّر الصوت في المذياع وإلى صوت وصورة في التلفاز فنسمعها ونراها بوضوح، في حين تتلاشى موجات الإذاعات والتلفاز الأخرى التي يختلف تردّدها عن تردّد الرنين. كما ألاحظ في المشهد المقابل. تُستخدم أجهزة الاتصال اللاسكي بشتى أنواعها في مجالات كثيرة،منها التواصل بين دوريات السير، واتصال الطائرات والسفن بالمراكز الأرضيّة، وغير |
|
مثال 15:
تتكوّن دارة استقبال في جهاز مذياع من مقاومة ومحثّ
محاثّته ( 1.4mH) ومواسع . أجد مواسعة المواسع المستخدم
لضبط المذياع على استقبال موجات محطة إذاعة عمان ( FM )
وتردّدها ( 99MHz ).
الحل:
حتى يتم الاستقبال، يجب أن يكون تردد دارة رنين المذياع
مطابقًا لتردّد موجات الإذاعة، أي هناك رنين: