رياضيات فصل أول

قسمة عدد كلي على كسر 

 

 

الفكرة الرئيسية : أقسم عددا كليا على كسر أو عدد كسري . 

 

 

تعلم : إذا كان ناتج ضرب عددين يساوي 1 , فإن كلاً منهما يسمى مقلوبا للآخر  , ويمكن إيجاد مقلوب الكسر بتبديل بسطه ومقامه .

أي أن ناتج ضرب الكسر في مقلوبه هو 1 .

 

وبما أن :         $\frac{\mathbf{2}}{\mathbf{7}}\mathbf{\times }\frac{\mathbf{7}}{\mathbf{2}}\mathbf{ } = \frac{1}{1} =1$                   إذن فإن كل من $\frac{2}{7}$ و $\frac{7}{2}$ مقلوبا للآخر   .                                           

 

       

                                                                                                                                             

مثال 1 : جد مقلوب كلا مما يأتي :

 

1 ) العدد 5 . الجواب : بما أن    $5\times \frac{1}{5}=1$      فإن مقلوب العدد 5 هو   $\frac{1}{5}$    .

2) العدد $\frac{7}{3}$ . الجواب : بما أن $\frac{7}{3}\times \frac{3}{7}=1$   فإن مقلوب العدد $\frac{7}{3}$ هو   $\frac{3}{7}$ .

---

* ويمكن استعمال المقلوب لإيجاد ناتج قسمة عدد كلي على كسر  وذلك بالضرب في مقلوب المقسوم عليه . 

 

$3÷\frac{1}{4}=12 \to \frac{3}{1}\times \frac{4}{1}=12$       

 

 

مثال 2 : جد ناتج ما يأتي :

$\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{2}\mathbf{÷}\frac{\mathbf{2}}{\mathbf{3}}$
أضرب في مقلوب $\frac{2}{3}$  وهو  $\frac{3}{2}$ .	$\mathbf{2}\mathbf{ }\mathbf{÷}\frac{\mathbf{2}}{\mathbf{3}}\mathbf{ }= 2\times \frac{3}{2}$
أكتب العدد الكلي في صورة كسر .	$= \frac{2}{1}\times \frac{3}{2}$
أضرب البسطين والمقامين وأكتب الناتج في أبسط صورة .	$=\frac{2\times 3}{1\times 2} =\frac{6÷2}{2÷2} = 3$

 

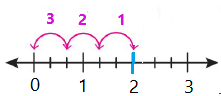
وللتحقق : يمكنني أن أتحقق من الحل باستعمال خط الأعداد وذلك بتقسيم المسافة بين كل عددين كليين متتالين إلى 3 أجزاء والعد قفزيا بمقدار $\frac{2}{3}$ ,

ألاحظ  أن عدد القفزات 3 أي أن          $2÷\frac{2}{3} = 3$ .

 

                                              

 

---

وعند قسمة عدد كلي على عدد كسري أحول العدد الكسري إلى كسر غير فعلي ويكون ناتج القسمة كالتالي :-

 

$\leftarrow$ أقل من 1 : إذا كان العدد الكلي أصغر من العدد الكسري .

$\leftarrow$أكبر من 1 :  إذا كان العدد الكلي أكبر من العدد الكسري .                                    

 

 

مثال 3 : لدى نجار قطعة خشب طولها  $m 6$ , يريد تقطيعها إلى أجزاء طول الجزء الواحد  $m \frac{1}{2}1$ , فكم قطعة تنتج لديه .

الجواب :

لإيجاد عدد القطع , أجد ناتج   $\frac{1}{2}1÷6$  .

 

أكتب 6 في صورة كسر  $\frac{6}{1}$ , و $1\frac{1}{2}$ في صورة كسر غير فعلي . أي أن $1\frac{1}{2} =\frac{3}{2}$	$\mathbf{6}\mathbf{ }\mathbf{÷}\mathbf{ }\mathbf{1}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{ }\mathbf{ }=\frac{6}{1}÷\frac{3}{2}$
أضرب في مقلوب الكسر $\frac{3}{2}$  وهو  $\frac{2}{3}$ .	$=\frac{6}{1}\times \frac{2}{3}$
أضرب البسطين والمقامين وأجد الناتج في أبسط صورة .	$= \frac{6\times 2}{1\times 3} = \frac{12÷3}{3÷3} = 4$

 

 

و يمكنني أن أتحقق من الحل باستعمال النماذج :

أرسم 6 مستطيلات .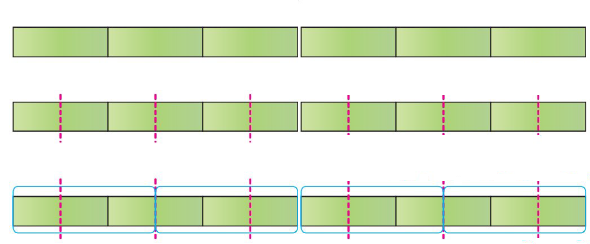
أقسم كل مستطيل الى جزأين متساويين .
أحوط كل  $\frac{1}{2}1$ من الأجزاء فيكون عدد مرات الإحاطة هو الناتج .

 

إذن نتج لدى النجار  4 قطع .