الرياضيات فصل أول

الدرس الثاني: مشتقتا الضرب والقسمة: 

سنتعلم في هذا الدرس :

1. إيجاد مشتقة ضرب اقترانين.

2. إيجاد مشتقة قسمة اقترانين.

3. إيجاد مشتقة المقلوب.

4. استخدام مشتقتا الضرب والقسمة مع قاعدة السلسلة.

أولًا: مشتقة ضرب اقترانين:

   يمكن إيجاد مشتقة حاصل ضرب اقترانين قابلين للاشتقاق $f\left(x\right)g\left(x\right)$ باستعمال النظرية الآتية:

        

 

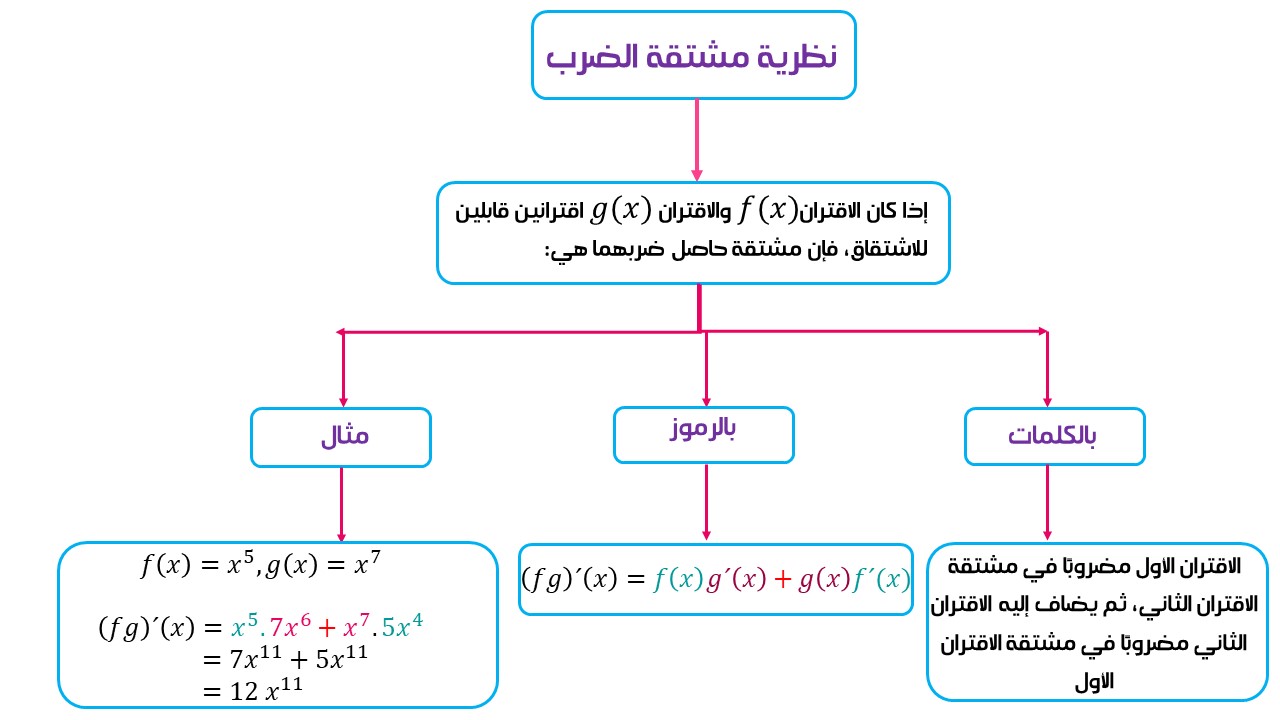
مثال: جد مشتقة كل اقتران مما يأتي:

          $\mathbf{1}\mathbf{)} f(x)=\left(x^4-3x\right)\left(2x^3+4\right) \mathbf{2}\mathbf{)} f\left(x\right)=\left(\sqrt[]{(x^3-7)}\right)\left(5x^2-6\right)$

 

الحل:

                                                                                                                                                                                                                                          

$\mathbf{2}\mathbf{)} f(x)=\left(\sqrt[]{(x^3-7)}\right)(5x^2-6)$
$f\left(x\right)=\left(\sqrt[]{(x^3-7)}\right)(5x^2-6)$	الاقتران المعطى
$f\text{'}\left(x\right)=\left(\sqrt[]{(x^3-7)}\right)\frac{d}{dx}(5x^2-6)+(5x^2-6)\frac{d}{dx}\left(\sqrt[]{(x^3-7)}\right)$	قاعدة مشتقة الضرب
$f\text{'}\left(x\right)=\left(\sqrt[]{(x^3-7)}\right)\left(10x\right)+(5x^2-6)\left(\frac{3x^2}{2 \sqrt[]{(x^3-7)}}\right)$	قواعد مشتقة اقتران القوة، مشتقة الجمع، مشتقة الطرح
$=10x \sqrt[]{(x^3-7)}+\frac{15x^4-18x^2}{2 \sqrt[]{(x^3-7)}}$	خاصية التوزيع والتبسيط

$\mathbf{1}\mathbf{)} f(x)=(x^4-3x)(2x^3+4)$
$f\left(x\right)=(x^4-3x)(2x^3+4)$	الاقتران المعطى
$f\text{'}\left(x\right)=\left(x^4-3x\right)\frac{d}{dx}\left(2x^3+4\right)+\left(2x^3+4\right)\frac{d}{dx}(x^4-3x)$	قاعدة مشتقة الضرب
$f\text{'}\left(x\right)=\left(x^4-3x\right)\left(6x^2\right)+\left(2x^3+4\right)\left(4x^3-3\right)$	قواعد مشتقة كثيرات الحدود، مشتقة الجمع، مشتقة الطرح
$=\left(6x^6-18x^3\right)+\left(8x^6+16x^3-6x^3-12\right)$	خاصية التوزيع
$=14x^6-8x^3-12$	التبسيط

 

* ملاحظة:

1. يمكن استخدام الخاصية التوزيعية أولًا عند إيجاد مشتقة ضرب اقترانين، ثم إيجاد مشتقة كل حد كما تعلمنا سابقًا.

2. $(f g)\text{'}(𝑥)\ne f\text{'}(𝑥) \times g\text{'}(𝑥)$

3. تذكر دائمًا قوانين الأسس لأنك ستحتاجها في خطوة التوزيع عند إيجاد مشتقة حاصل ضرب اقترانين، وأهمها:

a.  الأسس عند الضرب تُجمع:     $a^m\times a^n= a^{m+n}$ حيث $a\ne 0, 1$ ، $a, m, n$ أعداد حقيقية

b. الأسس عند الرفع لقوة تُضرب: ${\left(a^m\right)}^n=a^{mn}$ حيث $a, m, n ، a \ne 0, 1$ أعداد حقيقية

---

ثانيًا: مشتقة قسمة اقترانين:

            يمكن إيجاد مشتقة حاصل قسمة اقترانين قابلين للاشتقاق     $\frac{f\left(x\right)}{g\left(x\right)} , g\left(x\right)\ne 0$ باستعمال النظرية الآتية:

 

        

 

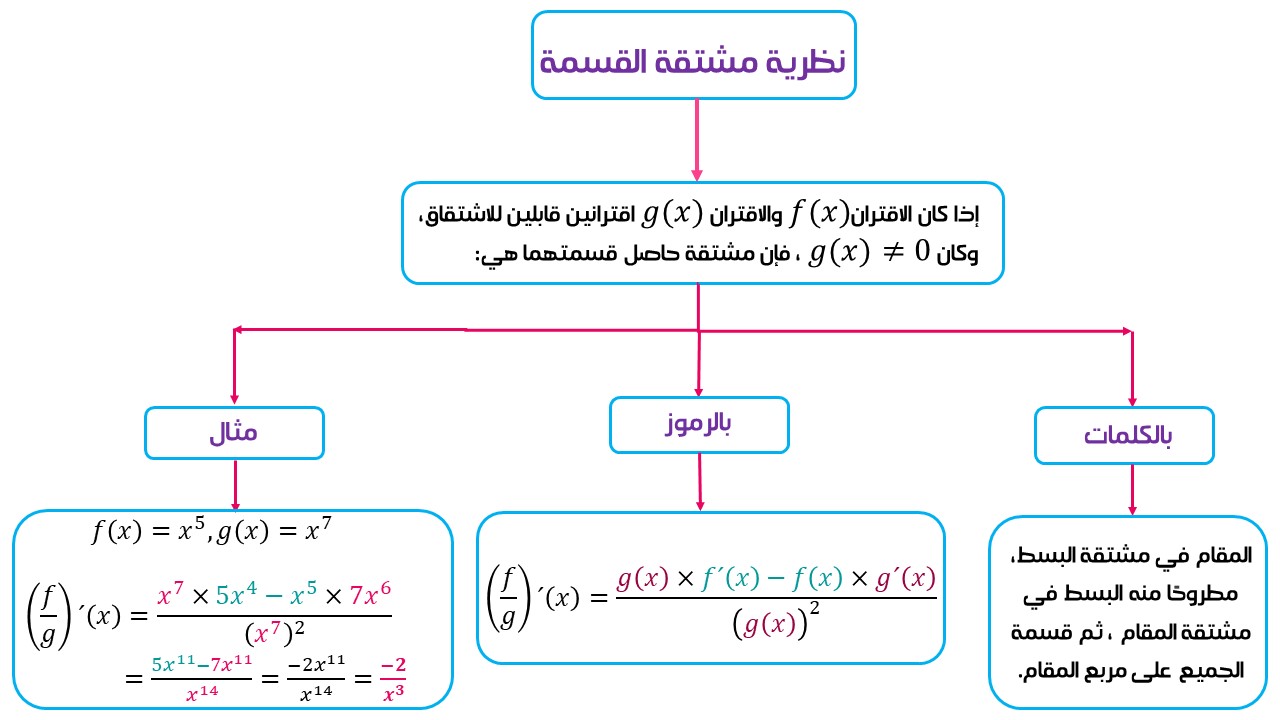
مثال: جد مشتقة كل اقتران مما يأتي:

         $\mathbf{1}\mathbf{)} f(x)=\frac{x^4}{2x^3+4} \mathbf{2}\mathbf{)} f\left(x\right)=\frac{5x^{-3}}{x^2-7}$

الحل:

 

$\mathbf{1}\mathbf{)} f(x)=\frac{x^4}{2x^3+4}$
$f\left(x\right)=\frac{x^4}{2x^3+4}$	الاقتران المعطى
$f\text{'}\left(x\right)=\frac{\left(2x^3+4\right){\displaystyle \frac{d}{dx}}\left(x^4\right) - \left(x^4\right)\frac{d}{dx}(2x^3+4)}{{\left(2x^3+4\right)}^2}$	قاعدة مشتقة القسمة
$=\frac{\left(2x^3+4\right)\left(4x^3\right) - \left(x^4\right)\left(6x^2\right)}{{\left(2x^3+4\right)}^2}$	قاعدتا مشتقة كثيرات الحدود، مشتقة الجمع.
$=\frac{\left(8x^6+16 x^3\right) - \left(6x^6\right)}{{\left(2x^3+4\right)}^2}$	خاصية التوزيع
$=\frac{2x^6+16 x^3 }{{\left(2x^3+4\right)}^2}$	التبسيط

$\mathbf{2}\mathbf{)} f(x)=\frac{x^{-3}}{x^2-7}$
$f\left(x\right)=\frac{x^{-3}}{x^2-7}$	الاقتران المعطى
$f\text{'}\left(x\right)=\frac{\left(x^2-7\right){\displaystyle \frac{d}{dx}}\left(x^{-3}\right) - \left(x^{-3}\right) {\displaystyle \frac{d}{dx}}(x^2-7)}{{\left(x^2-7\right)}^2}$	قاعدة مشتقة القسمة
$=\frac{(x^2-7)(-3 x^{-4}) - \left(x^{-3}\right) ( 2x)}{{(x^2-7)}^2}$	قاعدتا مشتقة كثيرات الحدود، مشتقة الجمع.
$=\frac{-3x^{-2}+21x^{-4} -2x^{-2} }{{(x^2-7)}^2}$	خاصية التوزيع
$=\frac{-5x^{-2}+21x^{-4} }{{(x^2-7)}^2}$	التبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

* ملاحظة:

1. $\left(\frac{f(𝑥)}{g(𝑥)}\right)\text{'} \ne \frac{f\text{'}(𝑥)}{g\text{'}(𝑥)}$

2. تذكر دائمًا قوانين الأسس لأنك ستحتاجها في خطوة التبسيط -أحيانًا-عند إيجاد مشتقة  قسمة اقترانين، وأهمها:

a.  الأسس عند القسمة تُطرح: $\frac{a^m}{a^n}= a^{m-n}$ حيث $a, m. n ،a\ne 0, 1$ أعداد حقيقية

b.  الأس السالب يقلب أساسه ليصبح موجبًا:  $a^{-n} =\frac{1}{a^n}$  

---

ثالثًا: مشتقة المقلوب:

باستعمال قاعدة مشتقة القسمة لاقترانين، يمكن إيجاد قاعدة عامة لمشتقة المقلوب،

حيث إنه إذا كان الاقتران $f\left(x\right)$ قابلًا للاشتقاق ، فإن مقلوبه $A\left(x\right)=\frac{1}{f\left(x\right)}$ , ومشتقة مقلوبه هي:

     قاعدة مشتقة القسمة          $A\text{'}\left(x\right)=\frac{f\left(x\right) \left(0\right)-\left(1\right) f\text{'}\left(x\right)}{{\left(f\left(x\right)\right)}^2}$

 

    بالتبسيط                                                     $A\text{'}\left(x\right)=\frac{- f\text{'}\left(x\right)}{{\left(f\left(x\right)\right)}^2}$

 

 

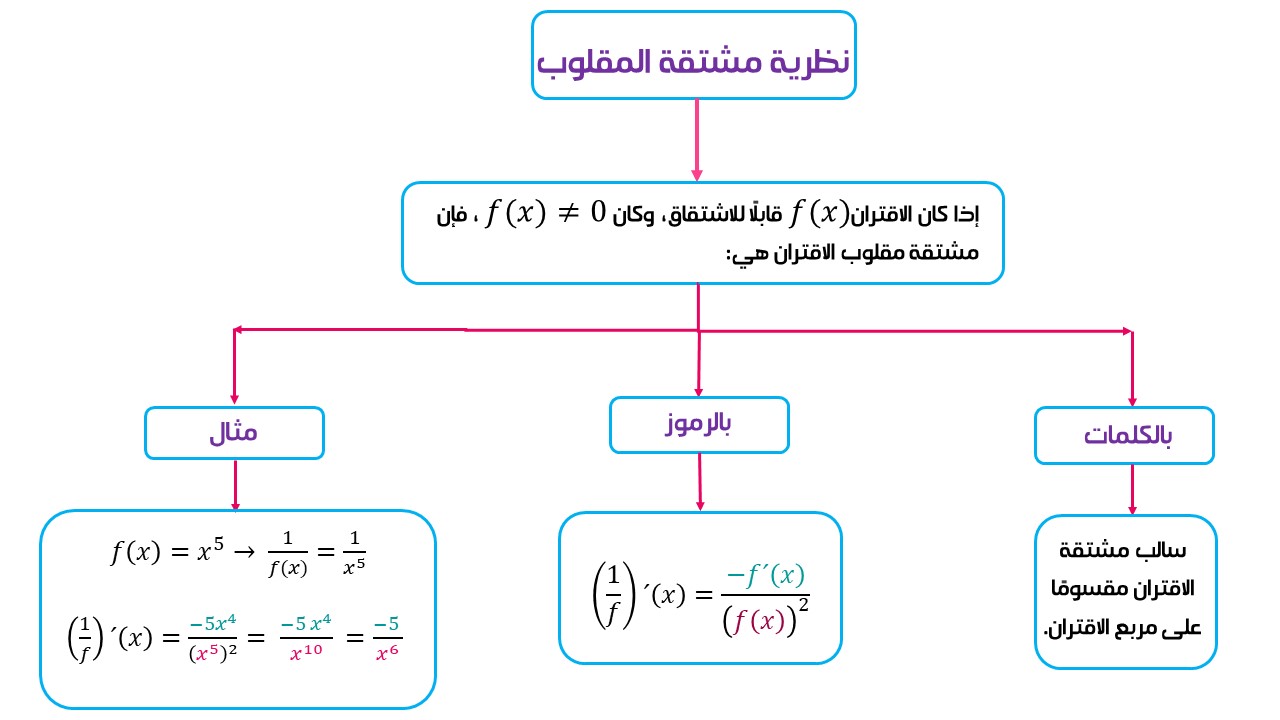
مثال: جد مشتقة كل اقتران مما يأتي:

          $\mathbf{1}\mathbf{)} f(x)=\frac{1}{5+3x^4} \mathbf{2}\mathbf{)} f\left(x\right)=\frac{-4}{7-2x^2}$

 

الحل:

 

$\mathbf{1}\mathbf{)} f(x)=\frac{1}{5+3x^4}$
$f\left(x\right)=\frac{1}{5+3x^4}$	الاقتران المعطى
$f\text{'}\left(x\right)=\frac{-{\displaystyle \frac{d}{dx}}(5+3x^4)}{{(5+3x^4)}^2}$	قاعدة مشتقة المقلوب
$=\frac{-12x^3}{{\left(5+3x^4\right)}^2}$	قاعدتا مشتقة اقتران القوة، مشتقة الجمع.

$\mathbf{2}\mathbf{)} f(x)=\frac{-4}{7-2x^2}$
$f\left(x\right)=\frac{-4}{7-2x^2}$	الاقتران المعطى
$f\text{'}\left(x\right)=\frac{\left(-4\right)\left(-{\displaystyle \frac{d}{dx}}\left(7-2x^2\right)\right)}{{\left(7-2x^2\right)}^2}$	قاعدة مشتقة المقلوب
$=\frac{\left(-4\right)\left(4x\right)}{{\left(7-2x^2\right)}^2}$	قاعدتا مشتقة كثيرات الحدود، مشتقة مضاعفات القوة.
$=\frac{-16x}{{(7-2x^2)}^2}$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

---

رابعًا: مشتقتا الضرب والقسمة، وقاعدة السلسلة:

 

 

 

 

 

لإيجاد مشتقة اقتران يمكنك استخدام قاعدة السلسلة - إن لزم الأمر - إضافة إلى تطبيق مشتقتي الضرب والقسمة.

ويمكن تذكر قاعدة السلسلة من خلال المخطط الآتي:

مثال: جد مشتقة كل اقتران مما يأتي:

            $a) f(x)= {\left(3x+9\right)}^7 {\left(6x-7\right)}^8 b) f\left(x\right)=\frac{2x-5}{{\left(5x-2\right)}^4}$

الحل:

 

$a) f(x)= {(3x+9)}^7 {(6x-7)}^8$
$f\left(x\right)= {(3x+9)}^7 {(6x-7)}^8$	الاقتران المعطى
$f\text{'}\left(x\right)={\left(3x+9\right)}^7 \frac{d}{dx}{\left(6x-7\right)}^8 +{(6x-7)}^8 \frac{d}{dx}{(3x+9)}^7$	قاعدة مشتقة الضرب
$={(3x+9)}^7 \times \left(8 {(6x-7)}^{7 }\left(6\right)\right) +{(6x-7)}^8 \times 7 {(3x+9)}^6\left(3\right)$	قاعدتا السلسلة، ومشتقة كثيرات الحدود
$=48 {(3x+9)}^7 {(6x-7)}^{7 } +21 {(6x-7)}^8 {(3x+9)}^6$	بالتبسيط
$=3 {(3x+9)}^6 {(6x-7)}^{7 } \left(16 (3x+9) + 7 (6x-7)\right)$	بإخراج ${(3x+9)}^6 {(6x-7)}^{7 }$ كعامل مشترك
$=3 {(3x+9)}^6 {(6x-7)}^{7 } \left( 48x+144 + 42x-49\right)$	باستعمال الخاصية التوزيعية
$=3 {(3x+9)}^6 {(6x-7)}^{7 } ( 90 x+95 )$	بالتبسيط

$b) f(x)=\frac{2x-5}{{(5x-2)}^4}$
$f\left(x\right)=\frac{2x-5}{{(5x-2)}^4}$	الاقتران المعطى
$f\text{'}\left(x\right)=\frac{{(5x-2)}^4 {\displaystyle \frac{d}{dx}}(2x-5)-(2x-5)\frac{d}{dx}{(5x-2)}^4}{{\left({(5x-2)}^4\right)}^2}$	قاعدة مشتقة القسمة
$=\frac{{(5x-2)}^4 {\displaystyle \times }\left(2\right)-(2x-5)\times 4{(5x-2)}^3 \left(5\right)}{{(5x-2)}^8}$	قاعدتا السلسلة، ومشتقة كثيرات الحدود
$=\frac{ 2 {(5x-2)}^4 -20 (2x-5){(5x-2)}^3 }{{(5x-2)}^8}$	بالتبسيط
$=\frac{ 2 {(5x-2)}^3 \left(\left(5x-2\right)-10 (2x-5)\right)}{{(5x-2)}^8}$	بإخراج ${(5x-2)}^3$ كعامل مشترك
$=\frac{ 2 {(5x-2)}^3 \left(5x-2-20x-50\right)}{{(5x-2)}^8}$	باستعمال الخاصية التوزيعية
$=\frac{ 2 (-15x-52)}{{(5x-2)}^5}$	بالتبسيط واستخدام قوانين الأسس عند القسمة

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---