امتحان الوحدة الاولى - عمر منصور - رياضيات علمي

1- بالاعتماد على الشكل المجاور جد قيم x التي تكون عندها المشتقة غير موجودة حيث الاقتران متصل عند هذه القيم وغير قابل للاشتقاق 

2- يتحرك جسيم في خط مستقيم وفق العلاقة $S\left(t\right)=\ln (t^2-2t+e)$ متى يعود الجسم الى موقعه الابتدائي

3- تتحرك كرة معلقة بالزنبرك للأعلى وللأسفل وفق العلاقة $S\left(t\right)=5 \sin t$ فإن تسارع الجسم عند السكون اللحظي

4- اذا كان $f\left(x\right)={\log }_2(x+\ln x)$ وكان $\ln 2= 0.7$ فإن $f^{\text{'}}\left(1\right)$

5- اذا كان $e^y-x=2$ فإن قيمة $y^{"}{(x+2)}^2$

6- اذا كان $f\left(x\right)=2e^{\sqrt{\tan x}}$ فان $f^{\text{'}}\left(\frac{\mathrm{\pi }}{4}\right)$

7- اذا كان $f\left(x\right)={\log }_{x}4$ وفإن $f^{\text{'}}\left(2\right)$ حيث $\ln 2=0.7$

8- اذا كان $g\left(x\right)=\sin \left(2x\right)$ وكان $f\left(x\right)=e^{\ln \left(\right(g\circ g\left)\right(x\left)\right)}$ فان $f^{\text{'}}\left(\mathrm{\pi }\right)$

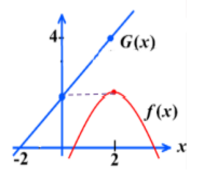
9- بالاعتماد على الشكل المجاور وكان $A\left(x\right)=F\left(x\right)G\left(x\right)$ فان $A^{\text{'}}\left(2\right)$

10- اذا كان $f\left(x\right)=\frac{1+5^{2x}}{\cos x}$ فجد $f^{\text{'}}\left(0\right)$

11- اذا كان $\frac{dx}{dt}=2$ و $y=se{c}^{2}t$ فان $\frac{d^{2}y}{d{x}^2}$ عند $t=\frac{\mathrm{\pi }}{4}$

12- اذا كان $f(2x^3+1)=x^2-\frac{1}{x}$ فان $f^{\text{'}}\left(3\right)$

13- اذا كان $(f^{\text{'}}\circ g)\left(3\right)=\mathrm{\pi }$ وكان $(f\circ g)\left(x\right)=\tan \left(\mathrm{\pi x}\right)$ فجد $g^{\text{'}}\left(3\right)$

14- اذا كان $f\left(x\right)=\frac{x^n}{3}$ وكان $a{x}^2=f^{\left(3\right)}\left(x\right)$ فجد $a$

15- اذا كان $f\left(x\right)=\frac{2(1-\sin x)}{\cos x}$ فان $f^{\text{'}}\left(x\right)$

16- اذا كان $4y^2-3xy=3x$ فان $\frac{dy}{dx}$ عند $y=1$

17- اذا كان للاقترن $f\left(x\right),g\left(x\right)$ مماس مشترك افقي عند النقطة $(2,3)$ وكان $h\left(x\right)=\frac{f^2\left(x\right)+3x^2}{g\left(x\right)}$ فجد معادلة المماس للعلاقة $h\left(x\right)$ عند $x=2$

18- اذا كان $f\left(x\right)=e^{ax+b}$ وكان ميل المماس عند النقطة $(1,2)$ يساوي 4 فان $f\left(x\right)$

19- اذا كان $y=x^x-1$ فجد $y^{\text{'}}{|}_{(x=1)}$

20- يمكن نمذجة الكمية $R$ (بالغرام) المتبقية من عينه كتلتها $200 g$ من عنصر مشع بعد t يوما باستعمال الاقتران $\Leftarrow$ $R\left(t\right)=200{(0.9)}^t$ أجد $\frac{dR}{dt}$ عندما $t=2$ لأقرب منزلتين عشريتين