رياضيات10 فصل أول

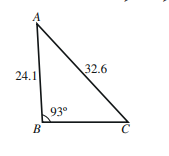
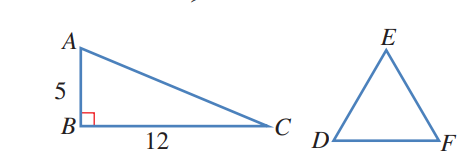أتحقق من فهمي صفحة 132

أجد مساحة المثلث بالوحدات المربعة في الشكل المجاور

الحل

قانون مساحة المثلث:

                   $K= \frac{1}{2}\times a\times b \times sinC$

$=\frac{1}{2}\times 5 \times 7 \times sin38 \approx 10.77$

---

أتحقق من فهمي صفحة 133

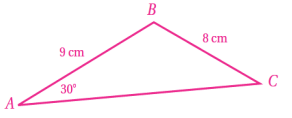
أجد مساحة المثلث $DEF$،علما بأن $EF=9cmو،DF=12cmو،DE=10cm$

الحل 

       $cos E =\frac{{\mathrm{e}}^2 - {\mathrm{d}}^2 - {\mathrm{f}}^2}{ -2\mathrm{df}}$

$= \frac{{12}^2 - 9^2 - {10}^2}{-2 \times 9 \times 10}$

$= \frac{144 -81 - 100}{-180}$

 $= \frac{-37}{-180} \approx 0.206$

$E = co{s}^{ -1} 0.206 = 78.14$

$K =\frac{1}{2}\times 10 \times 9 \times sin 78.14 = 44.08$

---

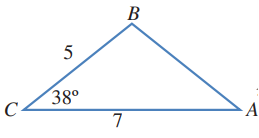
أتحقق من فهمي صفحة 133

قطعة رخام مثلثة الشكل،أبعادها$70cmو،85cmو،50cm$.ما مساحتها؟

الحل 

      $cos E = \frac{{\mathrm{e}}^{2 } - {\mathrm{d}}^2 - {\mathrm{f}}^2}{-2\mathrm{df}}$

$= \frac{{85}^{ 2} - {70}^2 -{50}^2}{-2 \times 50 \times 70}$

$=\frac{7225 - 4900 - 2500}{-7000}$   

        $= \frac{-175}{-700}\approx 0.025$

$E = cos{ }^{-1} 0.025 = 91.43$

$K = \frac{1}{2}\times 70 \times 50\times sin\left( 91.43\right) = 1749.45$

---

أتدرب وأحل المسائل صفحة 134

أجد مساحة كل من المثلثات الآتية:

1) المثلث $ABC$ الذي فيه $AC=8cmو،BC=7cm$،قياس الزاوية $ACB$ فيه $59°$

$K = \frac{1}{2} \times 8 \times 7 \times sin 59 = 24c{m}^2$

2) المثلث $ABC$ الذي قياس الزاوية $BAC$ فيه $AB=8cmو،AC=6.7cmو،85°$

$K = \frac{1}{2}\times 8 \times 6.7 \times sin 85 = 26.69c{m}^2$

3) المثلث $PQR$ الذي فيه $PR=19cmو،QR=27cm$،وقياس الزاوية $QRP$ فيه $109°$

$K = \frac{1}{2}\times 27 \times 19 \times sin 109 = 242.53c{m}^2$

4) المثلث $XYZ$ الذي فيه $XZ=191cmو،XY=231cm$،وقياس الزاوية $YXZ$ فيه $73°$

$K = \frac{1}{2}\times 231\times 191\times sin 73 = 21096.56c{m}^2$

5) المثلث $LMN$ الذي فيه $LM=39cmو،LN=63cm$،وقياس الزاوية $NLM$ فيه $85°$

$K = \frac{1}{2}\times 63 \times 39 \times sin 85 = 1223.83c{m}^2$

6) إذا كانت مساحة المثلث $ABC$ هي $BC=14cmو،27c{m}^2$، وقياس الزاوية $BCA$ فيه $115°$،فما طول  $\overline{AC}$؟

$K = \frac{1}{2}\times a \times b \times sin C$

$27 = \frac{1}{2}\times 14 \times b \times sin 115$

$27 = 7\times \sin 115 \times b$

$27 = 6.34 \times b$

$b = \frac{27}{6.34} = 4.26cm$

---

7) إذا كانت مساحة المثلث $LMN$ هي $133 c{m}^2$، $MN=21cmو،LM=16c{m}^2$،

والزاوية $LMN$ حادة،فما قياس كل من الزاويتين:$MNLو،LMN$؟

$K=\frac{1}{2}\times a\times b\times \sin C$

$133=\frac{1}{2}\times 21\times 16\times \sin C$

$133=168\times \sin C$

$\sin C=\frac{133}{168}=0.791$

$C={\sin }^{-1}0.791$

$$\begin{gathered} \angle LMN=C=52.28 \\ -------------------- \end{gathered}$$  

${\left(LN\right)}^2={\left(MN\right)}^2+{\left(ML\right)}^2-2\times MN\times ML\times \cos M$

${\left(LN\right)}^2={\left(21\right)}^2+{\left(16\right)}^2-2\times 21\times 16\times \cos 52.28$

${\left(LN\right)}^2=441+256-672\times 0.612$

${\left(LN\right)}^2=697-411.264$

${\left(LN\right)}^2=285.736$

$$\begin{gathered} LN=\sqrt{285.736}\approx 16.904cm \\ -------------------- \end{gathered}$$

$\frac{16}{\sin N}=\frac{16.904}{\sin 52.28}$

$\sin N=\frac{16\times \sin 52.28}{16.908}$

$\sin N=0.749$

$N={\sin }^{-1}\left(0.749\right)$

$\angle MNL=N=48.504$

---

8) لوحة على شكل مثلث،أطوال أضلاعه: $80cmو،70cmو،60cm$ . أجد مساحة اللوحة

$cos E = \frac{{\mathrm{e}}^2 - {\mathrm{d}}^2 - {\mathrm{f}}^2}{-2\mathrm{df}}$

$=\frac{{\left(70\right)}^2 -{\left(60\right)}^2 -{\left(80\right)}^2}{-2 \times 60 \times 80}$ 

$= \frac{4900 - 3600 - 6400}{-9600}$              

$= \frac{-5100}{-9600} \approx 0.531$

$E= cos{ }^{-1} ( 0.531) = 57.91$

$K= \frac{1}{2}\times 80 \times 60 \times sin (57.91) = 2033.315$

---

9) دائرتان، مركز إحداهما $P$ ومركز الأخرى $Q$،وطول نصف قطر إحداهما $6cm$ والأخرى $7cm$.

إذا تقاطعتا في النقطتين $Y و X$،وكان $PQ=9cm$،فما مساحة المثلث $PXQ$؟

$\cos X=\frac{9^2 -7^2 -6^2}{-2 \times 7 \times 6}$

$= \frac{81 - 49 - 36}{-84}$

$= \frac{-4}{-84} \approx 0.048$

$E= cos{ }^{-1} ( 0.048) = 87.27$

$K= \frac{1}{2}\times 7 \times 6 \times sin (87.27) = 20.98$

---

10) طائرة ورقية: صنع سليم طائرة ورقية كما في الشكل المجاور.

أجد مساحة المادة اللازمة لصنع الطائرة بالوحدات المربعة

$cos X =\frac{{\left(60\right)}^2 -{\left(40\right)}^2 -{\left(25\right)}^2}{-2 \times 40 \times 25}$

$= \frac{3600 - 1600 - 625}{-2000}$

$= \frac{-1375}{-2000} \approx 0.6875$

$E= cos{ }^{-1}(0.6875) = 46.57$

$K= \frac{1}{2}\times 40 \times 25 \times sin( 46.57) = 363.11$

$A=2\times 363.11 = 726.22$

---

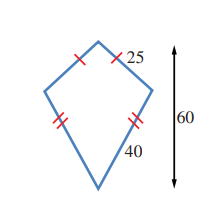
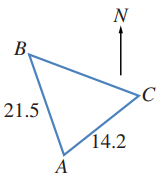
11) متنزه وطني: يراد إنشاء متنزه وطني على قطعة أرض مثلثة الشكل $ABC$.

إذا كانت النقطة $B$ في اتجاه $324°$ من النقطة $A$،والنقطة $C$ في اتجاه $042°$ من النقطة $A$،

فما مساحة المتنزه بالوحدات المربعة؟

$\angle BAC={78}^{\circ }$

$K = \frac{1}{2}\times 21.5 \times 14.2 \times sin\left(78\right)=149.31$

حقول:يمثل الشكل المجاور أبعاد حقل رباعي الأضلاع:

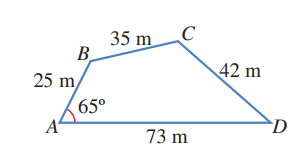
12) أثبت أن طول $BD$ هو $66m$،مقربا إجابتي إلى أقرب متر

13) أجد قياس الزاوية $C$

14) احسب مساحة الحقل

${\left(\mathrm{BD}\right)}^2 = {\left(25\right)}^2 +{\left(35\right)}^{2 } - 2\times 42 \times 35 \times cos C$

${\left(66\right)}^2 = 2989 - 2940 \times cos C$

$4350 = 2989 - 2940 cosC$

$4350 -2989 = -2940 cosC$

$1361 = -2940 cosC$

$cos C = \frac{1361}{-2940} = -0.463$

$C = co{s}^{ -1} (- 0.463)$

$C = 117.6$

$K_1=\frac{1}{2}\times 25\times 73\times \sin 65=912.5\times 0.906=826.7c{m}^2$

$K_2=\frac{1}{2}\times 35\times 42\times \sin 117.6=735\times 0.886=651.2c{m}^2$

$K=826.7+651.2=1477.9c{m}^2$

15) أحل المسألة الواردة في بداية الدرس

لدى مزارع قطعة أرض مثلثة الشكل ، طول أحد أضلاعها 84m ، وطول ضلع آخر 110m ،

وقياس الزاوية المحصورة بينهما $145°$ ، وقد أراد زراعتها بالبطاطا ، 

فلزمه 0.15kg من درنات البطاطا لكل متر مربع . كيف يستطيع المزارع حساب كمية درنات البطاطا اللازمة لزراعة أرضه ؟

$K =\frac{1}{2} \times 110 \times 84 \times \sin 145 = 2650$

$\mathrm{الكمية} : 2650 \times 0.15 = 397.5$

16) المثلث $ABC$ قائم الزاوية،والمثلث $DEF$ متطابق الأضلاع وللمثلثين المحيط نفسه.أجد مساحة المثلث $DEF$

 

$\left(A{C}^{ 2}\right) = {\left(12\right)}^{ 2} + {\left(5\right)}^{ 2} = 169$

$AC = 13$

$$\begin{gathered} \mathrm{يساوي} \mathrm{المثلث} \mathrm{محيط} \\ 13 +12 +5 = 30 \end{gathered}$$

${60}^{\circ }\mathrm{فيه} \mathrm{زاوية} \mathrm{أي} \mathrm{قياس}و10 \mathrm{الأضلاع} \mathrm{متساوي} \mathrm{المثلث} \mathrm{في} \mathrm{الضلع} \mathrm{طول}$

$K =\frac{1}{2 }\times 10 \times 10 \times sin 60 = 43.3$

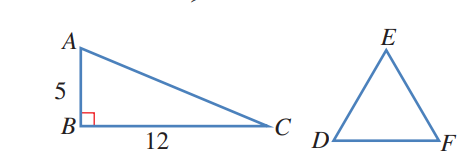
17) جغرافيا: برمودا منطقة مثلثة الشكل ، تقع في الجزء الغربي من المحيط الأطلسي، 

رؤوسها مدينة ميامي، وبرمودا، وسان خوان. وقد شهد مثلث برمودا وقوع عدد من حوادث اختفاء السفن و الطائرات.

إذا كانت المسافة بيم ميامي وسان خوان 1674km تقريبًا ، وبين ميامي وبرمودا نحو 1645km ،

وبين سان خوان وبرمودا قرابة 1544km ، فما مساحة مثلث برمودا من دون اعتبار لتقوس الأرض ؟ 

$cos X = \frac{{1544}^2 - {1674}^2 - {1645}^2}{-2 \times 1674 \times 1645}$

$=\frac{2383936 - 2802276 - 2706025}{-5507460 }$

$=\frac{-3124365}{-5507460}\approx 0.567$

$X = co{s}^{-1} 0.567 = 55.46$

$K =\frac{1}{2}\times 1674 \times 1645 \times sin 55.46 = 1134165.78$

مهارات التفكير العليا

18. تحد : أجد مساحة المثلث ABC الذي قياس الزاوية A فيه $70°$ ، 

وقياس الزاوية B فيه $60°$ ، وطول الضلع AB فيه 4cm . 

$\angle ACB=50$

$\frac{4}{\sin 50} =\frac{\mathrm{a}}{\sin 70}$

$a =\frac{4 \sin 70}{\sin 50}= 4.9$

$K =\frac{1}{2} \times 4.9 \times 4 \times \sin 60$

$K = 8.49$

 

19. أكتشف الخطأ : ABC مثلث فيه AB = 9cm, BC = 8cm  ، وقياس الزاوية A فيه $30°$ .

أرادت نور إيجاد مساحته إلى أقرب عشر ، فكان حلها كما يأتي : 

$K =\frac{1}{2} \times 8 \times 9 \times sin30° = 18 c{m}^2$

أخطأت نور حين جعلت الزاوية A محصورة بين الضلعين المعلومين 

الزاوية المحصورة بين الضلعين المعلومين هي  B 

$\frac{\mathrm{sinC}}{9} = \frac{\sin 30}{8}$

$C= 34.2 and B=115.8$

$A= \frac{1}{2}\times 9\times 8\times sin115.8 =32.4$ 

---

---

كتاب التمارين 

أجد مساحة المثلث في كل من الحالات الآتية : 

1. المثلث  ABC  فيه AB = 8cm , و AC = 11cm و $m\angle CAB = 67°$

$K = \frac{1}{2}\times AB \times AC \times \sin 67$

$=\frac{1}{2}\times 8 \times 11\times \sin 67=40.5 c{m}^2$

2. المثلث  PQR فيه PQ = 30cm , و PR = 22cm و $m\angle QPR = 120°$

$K =\frac{1}{2}\times 30 \times 22\times \sin 120=285.8 c{m}^2$

3. المثلث  XYZ فيه XY= 12cm , و XZ = 15cm و YZ = 10cm 

${10}^2 = {12}^2 + {15}^2 - 2\left(12\right)\left(15\right) cosx$

$100 = 144 +225 -360 cosx$

$cosx = 0.74 \Rightarrow x = 42.3$

$K =\frac{1}{2}\times 12 \times 15\times \sin 42.3=60.6 c{m}^2$

4. المثلث  LMN فيه LM = 25cm , و LN = 14cm وMN = 18cm 

${14}^2 = {18}^2 + {25}^2 - 2\left(18\right) \left(25\right) cos M$

$cos M= 0.83 \Rightarrow M= 33.9°$

$K =\frac{1}{2}\times 18 \times 25\times \sin 33.9=125.5 c{m}^2$

5. مساحة المثلث ABC هي $84c{m}^2$ . إذا كان BC = 15 cm و $m\angle BCA = 120°$ فما طول $\overline{AC}$ ؟

$K = 84cm$

$84 =\frac{1}{2} \left(15\right)\left(\mathrm{AC}\right) sin 120$

$AC= 12.9 cm$

6. مساحة المثلث DEF هي $100 {\mathrm{cm}}^2$ إذا كان DE = 14cm و $m\angle DEF = 64°$ فما طول $\overline{EF}$ ؟ 

$K =\frac{1}{2}\times ED \times EF\times \sin E$

$100=\frac{1}{2}\times \left(17\right)\times \left(\mathrm{EF}\right) \sin 64$

$EF = 15.9 cm$

7. أجد مساحة المثلث PQR إذا كان $m\angle QRP = 75°$ و $m \angle PQR = 60°$ و PQ = 12cm . 

$m\angle RPQ = 180 -60 -75 = 45$

$\frac{12}{\sin 75}=\frac{\mathrm{PR}}{\sin 60}\Rightarrow PR= 10.8$

$K =\frac{1}{2}\times 12 \times 10.8\times \sin 45=45.7 c{m}^2$

8. أجد مساحة المثلث EFG إذا كان $m\angle GEF = 63°$ و $m \angle EFG = 45°$ و EF = 46cm . 

$m\angle EGF = 180-63-45 = 72$

$\frac{\mathrm{EG}}{\sin 45}= \frac{46}{\sin 72}\Rightarrow EG = 34.2$

$K =\frac{1}{2}(34.2)\left(46\right) \sin 63 =700.87 c{m}^2$

9. أجد مساحة المنطقة المظللة في الشكل المجاور بالوحدات المربعة ، علمًا بأن الشكل نصف دائرة . 

$QR=\sqrt{{26}^2 - {24}^{ 2}} =10$

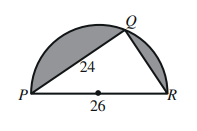
مساحة المنطقة المظللة = مساحة نصف الدائرة - مساحة المثلث القائم PQR

$= 0.5\times {13}^2 \times \mathrm{\pi } - 0.5 \times 24 \times 10\approx 145.5$

---

10 . أجد مساحة النافذة ذات الأبعاد المبينة في الشكل المجاور بالوحدات المربعة . 

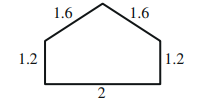
قياس زاوية رأس المثلث $\mathbf{77}\mathbf{.}\mathbf{4}\mathbf{°}$ تقريبًا 

مساحة النافذة = مساحة المثلث +  مساحة المستطيل 

$= 0.5 \times 1.6 \times 1.6 \times sin77.4° + 2\times 1.2\approx 3.65$

---

أجد مساحة كل من المثلثين الآتيين بالوحدات المربعة : 

11.

 

$\frac{25}{\sin \mathrm{M} }= \frac{18}{\sin 40°} \Rightarrow M \approx 63.2°$

$N\approx 76.8°$

$K = 0.5\times 25\times 18 \times sin 76.8° \approx 219$

---

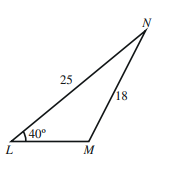
12. 

$\frac{32.6}{\sin (93°) }= \frac{24.1}{\sin C} \Rightarrow C \approx 47.6°$

$and A \approx 39.4°$

$K = 0.5\times 32.6\times 24.1 \times \sin (39.4°) \approx 249.3$