الاحتمالاتُ وأشكالُ فِنْ

الاحتمالاتُ وأشكالُ فِنْ

Probabilities and Venn diagrams

فكرةُ الدرسِ : إيجادُ الاحتمالِ باستعمالِ أشكالِ فِنْ.

 

أولًا : التعبيرُ بالرموزِ عنْ حوادثَ مُمثَّلةٍ بأشكالِ فِنْ

 

تعلَّمْتُ سابقًا أشكالَ فِنْ، واستعملْتُها لتمثيلِ البياناتِ؛ وذلكَ بتنظيمِها في مجموعتينِ أوْ أكثرَ باستعمالِ منحنياتٍ

مُغلَقةٍ مُتداخِلةٍ (متقاطعةٌ)؛ إذْ يُشكِّلُ كلُّ منحنٍ مجموعةً مستقلةً منَ البياناتِ، ويُمثِّلُ الجزءُ المُتداخِل بينَ المنحنيينِ

البياناتِ المشتركةَ بينَ المجموعتينِ.

 

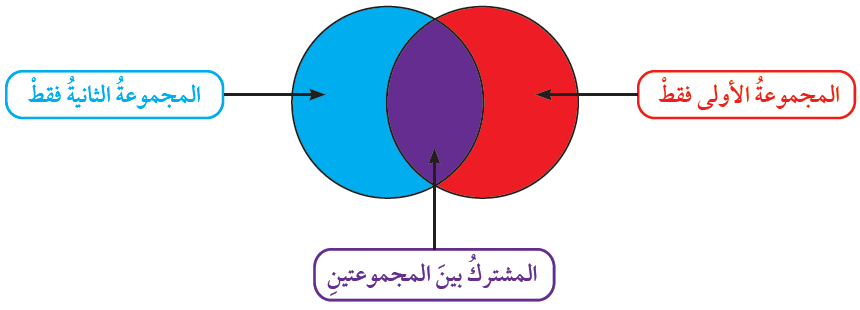
•• يُمكِنُ استعمالُ أشكالِ فِنْ للتعبيرِ عنْ حوادثِ تجربةٍ عشوائيةٍ بيانيًّا، وذلكَ لتسهيلِ إيجادِ احتمالاتِ هذهِ الحوادثِ.

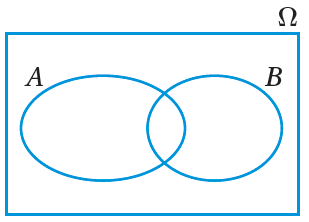
فمثلاً، إذا كانَ A و B حادثينِ في تجربةٍ عشوائيةٍ، فإنَّهُ يُمكِنُ تمثيلُهُما باستعمالِ أشكالِ فِنْ، وذلكَ برسمِ مستطيلٍ يُمثِّلُ الفضاءَ العينيَّ للتجربةِ،  ثمَّ رسمِ منحنى مُغلَقٍ يُمثِّلُ الحادثَ A ، ورسمِ منحنى آخرَ مُغلَقٍ يُمثِّلُ الحادثَ B.

 

 

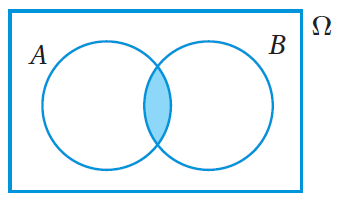
تُمثِّلُ المنطقةُ المُظلَّلةُ في شكلِ فِنْ المجاورِ تقاطعَ الحادثِ A والحادثِ B، ويُمكِنُ التعبيرُ عنْها بالرمزِ A∩B. أتعلَّمُ : تقاطعُ الحادثِ A والحادثِ B يعني وقوعَهُما معًا.

 

 

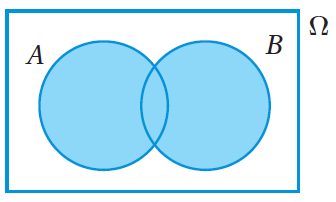
أمّا المنطقةُ المُظلَّلةُ في شكلِ فِنْ المجاورِ فتُمثِّلُ  اتحادَ الحادثِ A والحادثِ B، ويُمكِنُ التعبيرُ عنْها بالرمزِ  A∪B. أتعلَّمُ : اتحادُ الحادثِ A والحادثِ B يعني وقوعَ الحادثِ A، أوْ وقوعَ الحادثِ B، أوْ وقوعَ الحادثينِ معًا.

 

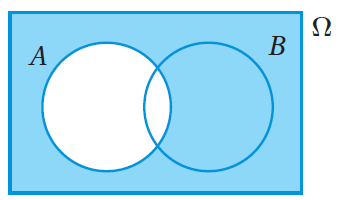
في حينِ تُمثِّلُ المنطقةُ المُظلَّلةُ في الشكلِ المجاورِالحادثَ المُتمِّمَ  (complement event)للحادثِ A، ويُمكِنُ التعبيرُ عنْهُ بالرمزِ $\overline{A}$  أتعلَّمُ : لأيِّ تجربةٍ عشوائيةٍ، فإنَّ $\overline{A}$ يعني عدمَ وقوعِ الحادثِ $A$

 

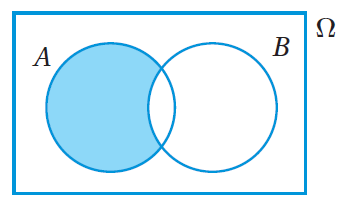
وأمّا الحادثُ الذي تُمثِّلُهُ المنطقةُ المُظلَّلةُ في الشكلِ المجاورِ فهوَ وقوعُ الحادثِ A فقطْ، وعدمُ وقوعِالحادثِ B، ويُمكِنُ التعبيرُ عنْ هذا الحادثِ بالرمزِ A - B. أتعلَّمُ : يُمكِنُ أيضًا التعبيرُ عنِ الحادثِ A - B بالرمزِ $A\cap \overline{B}$

 

مثال 1 : 

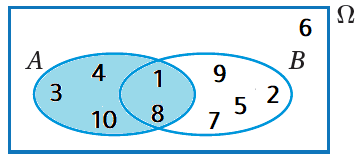
أُعبِّرُ بالرموزِ عنِ الحادثِ الذي تُمثِّلُهُ المنطقةُ المُظلَّلةُ في كلٍّ منْ أشكالِ فِنْ الآتيةِ :

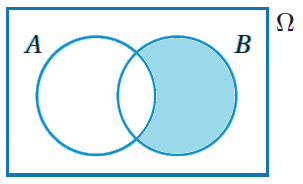
أُلاحِظُ أنَّ المنطقةَ المُظلَّلةَ في الشكل المجاورِ تُعبر عن وقوعُ الحادثِ B فقطْ، وعدمُ وقوعِ الحادثِ A، ويُمكِنُ التعبيرُ عنْ هذا الحادثِ بالرمزِ $B-A$ أو الرمز $B\cap \overline{A}$
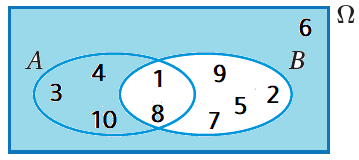
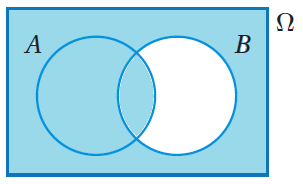
أُلاحِظُ أنَّ المنطقةَ المُظلَّلةَ تُعبِّرُ عنِ اتحادِ مُتمِّمةِ الحادثِ B والحادثِ A ؛ لذا يُمكِنُ التعبيرُ عنْ هذا الحادثِ بالرمزِ  $\overline{B}\cup A$

 

ثانيًا : إيجادُ احتمالاتِ حوادثَ لتجاربَ عشوائيةٍ مُمثَّلةٍ بأشكالِ فِنْ

تعلَّمْتُ سابقًا أنَّهُ إذا كانَتِ التجربةُ العشوائيةُ متساويةَ الاحتمالِ، فإنَّ احتمالَ وقوعِ أيِّ حادثٍ فيها يساوي نسبةَ عددِ

عناصرِ الحادثِ إلى عددِ عناصرِ الفضاءِ العينيِّ.

$\mathrm{P}\left(\mathrm{A}\right) = \frac{ \mathrm{A} \mathrm{الحادث} \mathrm{عناصر} \mathrm{عدد}}{\mathrm{العيني} \mathrm{الفضاء} \mathrm{عناصر} \mathrm{عدد}}$

 

بما أنَّ الفضاءَ العينيَّ Ω هوَ مجموعةٌ تحوي جميعَ النواتجِ التي يُتوقَّعُ حدوثُها عندَ إجراءِ تجربةٍ عشوائيةٍ ما، فإنَّ احتمالَ

الفضاءِ العينيِّ هوَ 1 ؛ أيْ إنَّ P(Ω) = 1 . ولهذا، فإنَّ احتمالَ الحادثِ المُتمِّمِ لأيِّ حادثٍ في الفضاءِ العينيِّ، مثلَ A ، هوَ 1 ناقصُ

احتمالِ وقوعِ الحادثِ A .

مفهومٌ أساسيٌّ (احتمالُ الحادثِ المُتمِّمِ)

بالكلماتِ: احتمالُ وقوعِ مُتمِّمةِ الحادثِ A هوُ 1 ناقصُ احتمالِ وقوعِ الحادثِ. بالرموزِ : لأيِّ حادثٍ(A) في تجربةٍ عشوائيةٍ، فإنَّ: $P\left(\overline{A}\right) = 1 - P\left(A\right)$

 

•• يُمكِنُ استعمالُ المفاهيمِ السابقةِ لإيجادِ احتمالاتِ حوادثَ مُمثَّلةٍ بأشكالِ فِنْ.

مثال 2 : 

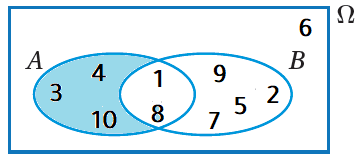
كُتِبَتِ الأعدادُ الصحيحةُ منْ 1 إلى 10 على مجموعةٍ منَ البطاقاتِ المُتطابِقةِ ، ثمَّ اختيرَتْ بطاقةٌ عشوائيًّا، ومُثِّلَ الفضاءُ العينيُّ لهذهِ التجربةِ العشوائيةِ التي تحوي الحادثينِ A و B في شكلِ فِنْ المجاورِ. أجدُ كُلًّ منَ الاحتمالاتِ الآتيةِ : $$\begin{gathered} 1) P(A) 2) P\left(\overline{B}\right) \\ 3) P(A-B) 4) P(\overline{A}\cap B) \end{gathered}$$

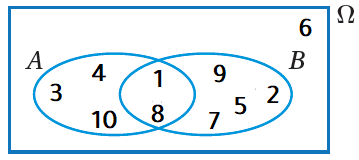الحل : 

بما أنَّ عددَ عناصرِ الفضاءِ العينيِّ هوَ 10، وعددَ عناصرِ الحادثِ A هوَ 5 كما يظهرُ في المنطقةِ المُظلَّلةِ منَ الشكلِ المجاورِ، فإنَّ : $P\left(A\right) = \frac{5}{10}=\frac{\mathbf{1}}{\mathbf{2}}$

$\mathbf{1}\mathbf{)}\mathbf{ }P(\mathrm{A})\mathbf{ }\mathbf{ }$

 

صيغةُ احتمالِ المُتمِّمةِ $P\left(\overline{B}\right) = 1 - P\left(B\right)$ بالتعويضِ                         $P\left(\overline{B}\right) = 1 - \frac{6}{10}$  بالتبسيطِ                           $=\frac{4}{10}=\frac{\mathbf{2}}{\mathbf{5}}$

$\mathbf{2}\mathbf{)}\mathbf{ }P(\overline{B})$

 

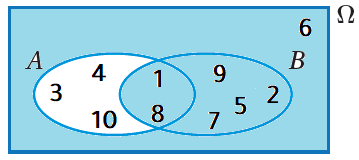
وقوعُ الحادثِ A فقطْ، وعدمُ وقوعِ الحادثِ B ، وعدد عناصر A - B ، هو 3 إذن :  $P(A-B) = \frac{\mathbf{3}}{\mathbf{10}}$

$\mathbf{3}\mathbf{)} P(A-B)$

 

بما أنَّ عددَ عناصرِ هذا الحادثِ هوَ 7 كما يظهرُ في المنطقةِ المُظلَّلةِ منَ الشكلِ المجاورِ، فإنَّ:                     $P(\overline{A}\cap B) = \frac{\mathbf{7}}{\mathbf{10}}$

$\mathbf{4}\mathbf{)} P(\overline{A}\cap B)$

 

---

 

استعمالُ أشكالِ فِنْ لإيجادِ احتمالاتِ حوادثَ لتجاربَ عشوائيةٍ

يُمكِنُ استعمالُ أشكالِ فِنْ لتسهيلِ إيجادِ احتمالاتِ حوادثَ لتجاربَ عشوائيةٍ تُمثِّلُ مواقفَ حياتيةً.

مثال 3 : 

تقدَّمَ 50 طالب منْ طلبةِ الصفِّ التاسعِ في إحدى المدارسِ لامتحانٍ وطنيٍّ يقيسُ قدراتِهِمْ في مادتيِ اللغةِ العربيةِ

والرياضياتِ. نجحَ منْ هؤلاءِ الطلبةِ 35 طالبًا في مادةِ اللغةِ العربيةِ، و 30 طالبًا في مادةِ الرياضياتِ. أمّا عددُ الطلبةِ

الناجحينَ في المادتينِ معًا فبلغَ 20 طالبًا:

1) أُمثِّلُ البياناتِ بشكلِ فِنْ.

2) إذا اختيرَ أحدُ الطلبةِ المُتقدِّمينَ عشوائيًّا، فأجدُ احتمالَ أنْ يكونَ هذا الطالبُ ناجحًا في إحدى المادتينِ على الأقلِّ.

3) إذا اختيرَ أحدُ الطلبةِ المُتقدِّمينَ عشوائيًّا، فأجدُ احتمالَ أنْ يكونَ هذا الطالبُ ناجحًا في مادةِ اللغةِ العربيةِ فقطْ.

الحل : 

1) أُمثِّلُ البياناتِ بشكلِ فِنْ.

الخطوةُ 1 : أُحدِّدُ الحوادثَ المذكورةَ في التجربةِ العشوائيةِ.

أفترضُ أنَّ A هوَ حادثُ اختيارِ طالبٍ ناجحٍ في مادةِ اللغةِ العربيةِ، وأنَّ B هوَ حادثُ اختيارِ طالبٍ ناجحٍ في مادةِ الرياضياتِ.

الخطوةُ 2 : أُمثِّلُ الفضاءَ العينيَّ والحوادثَ بشكلِ فِنْ.

· أُحدِّدُ عددَ الطلبةِ الناجحينَ في مادةِ اللغةِ العربيةِ فقطْ، وذلكَ بطرحِ عددِ الطلبةِ الناجحينَ في المادتينِ معًا منْ عددِ

الطلبةِ الناجحينَ في مادةِ اللغةِ العربيةِ $\left(A\right)$:

                                                 $35 - 20 = 15$                                                                                             

 

· أُحدِّدُ عددَ الطلبةِ الناجحينَ في مادةِ الرياضياتِ فقطْ، وذلكَ بطرحِ عددِ الطلبةِ الناجحينَ في المادتينِ معًا منْ عددِ الطلبةِ

الناجحينَ في مادةِ الرياضياتِ $\left(B\right)$:

                                                                  $30- 20 = 10$        

• أُحدِّدُ عددَ الطلبةِ الذينَ لمْ ينجحوا في أيٍّ منَ المادتينِ، وذلكَ بطرحِ عددِ الطلبةِ الناجحينَ في مادةِ اللغةِ العربيةِ فقطْ،

وعددِ الطلبةِ الناجحينَ في مادةِ الرياضياتِ فقطْ، وعددِ الطلبةِ الناجحينَ في المادتينِ معًا، منَ العددِ الكليِّ للطلبةِ:

                                                                   $50 -(15+10+20) = 5$

 

· أُمثِّلُ هذهِ البياناتِ بشكلِ فِنْ كالآتي:                         

                                                                   

 

---

 

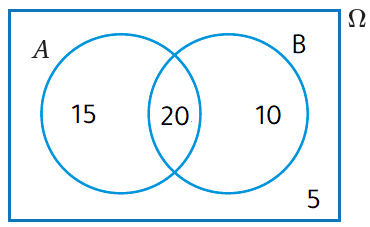
2) إذا اختيرَ أحدُ الطلبةِ المُتقدِّمينَ عشوائيًّا، فأجدُ احتمالَ أنْ يكونَ هذا الطالبُ ناجحًا في إحدى المادتينِ على الأقلِّ.

إنَّ كلمتيْ(على الأقلِّ) في السؤالِ تشيرانِ إلى أنَّ المطلوبَ هوَ اتحادُ الحادثِ A والحادثِ B كما في الشكلِ المجاورِ. إذنْ:       $P(A\cup B) = \frac{45}{50}=\frac{\mathbf{9}}{\mathbf{10}}$

 

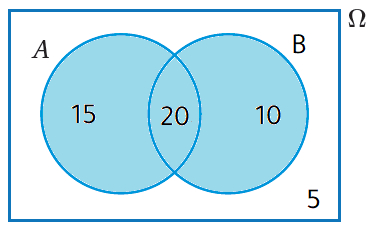3) إذا اختيرَ أحدُ الطلبةِ المُتقدِّمينَ عشوائيًّا، فأجدُ احتمالَ أنْ يكونَ هذا الطالبُ ناجحًا في مادةِ الرياضيات فقطْ.

إنَّ احتمالَ أنْ يكونَ الطالبُ ناجحًا في مادةِ الرياضيات فقطْ يعني إيجادَ احتمالِ المنطقةِ المُظلَّلةِ في شكلِ فِنْ المجاورِ. إذنْ: $P(B-A) = \frac{10}{50} = \frac{\mathbf{1}}{\mathbf{5}}$

 

---

 

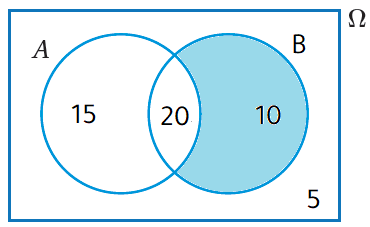ثالثًا : الحوادثُ المتنافيةُ

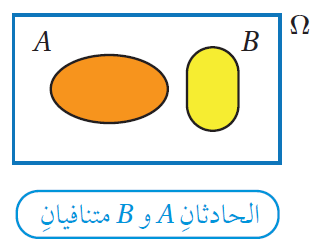
الحوادثُ المتنافيةُ (mutually exclusive events) : هيَ الحوادثُ التي لا يُمكِنُ وقوعُها معًا؛ ما يعني عدمَ وجودِ عناصرَ مشتركةٍ بينَها. فمثلًا ، عندَ رميِ حجرِ نردٍ مَرَّةً واحدةً، فإنَّ حادثَ ظهورِ العددِ 5 لا يُمكِنُ أنْ يقعَ معَ حادثِ ظهورِ العددِ 6 في الوقتِ نفسِهِ، وهذا يعني أنَّ تقاطعَهُما هوَ ∅، وأنَّ احتمالَ تقاطعِهِما هوَ صفرٌ.

 

مثال 4 : 

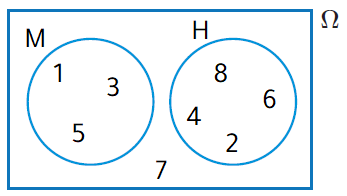
كُتِبَتِ الأعدادُ الصحيحةُ منْ 1 إلى8 على مجموعةٍ منَ البطاقاتِ المُتطابِقةِ، ثمَّ اختيرَتْ بطاقةٌ عشوائيًّا، ومُثِّلَ الفضاءُ العينيُّ لهذهِ التجربةِ العشوائيةِ التي تحوي الحادثينِ H و M في شكلِ فِنْ المجاورِ. أجدُ كُلًّ منَ الاحتمالاتِ الآتيةِ : $1) P(M\cap H) 2) P(M\cup H) 3) P(M-H)$

 الحل : 

  $\mathbf{1}\mathbf{)} P(M\cap H)$

أُلاحِظُ منْ شكلِ فِنْ أنَّ الحادثَ M والحادثَ H متنافيانِ؛ لأنَّهُ لا توجدُ عناصرُ مشتركةٌ بينَهُما. إذنْ : 

                     $P(M\cap H) = \frac{0}{8} = \mathbf{0}$

 

$\mathbf{2}\mathbf{)}\mathbf{ }P(M\cup H)$

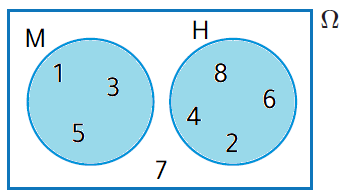
بما أنَّ الحادثَ M والحادثَ H متنافيانِ، فإنَّ M ∪ H يعني وقوعَ الحادثِ M فقطْ، أوْ وقوعَ الحادثِ H فقطْ؛ لأنَّهُما لا يقعانِ معًا. ومنْ ثَمَّ، فإنَّ عددَ عناصرِ هذا الحادثِ هوَ 7 كما يظهرُ في المنطقةِ المُظلَّلةِ منَ الشكلِ المجاورِ. إذنْ، احتمالُ الحادثِ M ∪ H هوَ: $P(M\cup H) = \frac{\mathbf{7}}{\mathbf{8}}$

 

$\mathbf{3}\mathbf{)} P(M-H)$

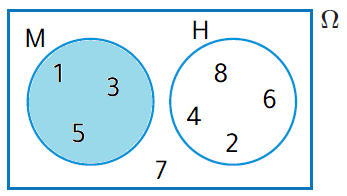
بما أنَّ الحادثَ M والحادثَ H متنافيانِ، فإنَّ M - H يعني وقوعَ الحادثِ M فقطْ؛ لأنَّهُما لا يقعانِ معًا كما يظهرُ في المنطقةِ المُظلَّلةِ منَ الشكلِ المجاورِ. إذنْ :  $P(M-H) = \frac{\mathbf{3}}{\mathbf{8}}$

 

---

 

الحوادثُ المتنافيةُ الشاملةُ
 

الحوادثُ الشاملةُ ( exhaustive events) هيَ الحوادثُ التي يُشكِّلُ اتحادُ نواتجِها المُحتمَلةِ الفضاءَ العينيَّ كاملًا. فمثلًا، عندَ

إلقاءِ حجرِ نردٍ، فإنَّ حادثَ ظهورِ عددٍ أكبرَ منْ 3 وحادثَ ظهورِ عددٍ أقلَّ منْ 5 يُمثِّلانِ حادثينِ شاملينِ.

قدْ تكونُ بعضُ الحوادثِ متنافيةً وشاملةً. فمثلًا ، عندَ رميِ حجرِ نردٍ، فإنَّ حادثَ ظهورِ عددٍ فرديٍّ وحادثَ ظهورِ عددٍ زوجيٍّ

يُمثِّلانِ حادثينِ متنافيينِ؛ لأنَّهُ لا يُمكِنُ أنْ يقعا معًا. وهما أيضًا حادثانِ شاملانِ؛ لأنَّ نواتجَهُما المُحتمَلةَ تُشكِّلُ الفضاءَ

العينيَّ كاملًا.

 

يُظهِرُ شكلا فِنْ الآتيانِ كُلًّ منَ الحوادثِ المتنافيةِ، والحوادثِ الشاملةِ، والحوادثِ المتنافيةِ والشاملةِ :

 

•• إذا كانَتِ الحوادثُ متنافيةً وشاملةً، فإنَّ مجموعَ احتمالاتِها هوَ 1.

•• أتعلم  : مجموعُ احتمالاتِ الحوادثِ المتنافيةِ والشاملةِ هوَ 1، أمّا الحوادثُ الشاملةُ غيرُ المتنافيةِ فيكونُ مجموعُ احتمالاتِها أكبرَ منْ 1.

مثال 5 :  

قرصٌ دائريٌّ مُقسَّمٌ إلى 5 قطاعاتٍ غيرِ مُتطابِقةٍ، ومُلوَّنةٍ بالأحمرِ والأصفرِ والأزرقِ والأخضر والأبيض . إذا كانَ الجدولُ

المجاورُ يُبيِّنُ احتمالَ توقُّفِ المُؤشِّرِ عندَ كلِّ لونٍ منْ هذهِ الألوانِ، فأجدُ قيمةَ$x$.

الأبيض	الأخضر	الأزرق	الأصفر	الأحمر	اللون
$2x$	0.3	$x$	0.17	0.2	الاحتمال

الحل : 

بما أنَّ حوادثَ توقُّفِ مُؤشِّرِ القرصِ على الألوانِ الخمسة هيَ حوادثُ متنافيةٌ وشاملةٌ، فإنَّ مجموعَ احتمالاتِها هوَ 1:

مجموعُ احتمالات الحوادثِ الشاملةِ	$0.2 + 0.17 + x + 0.3 + 2x = 1$
بجمعِ الثوابتِ، وجمعِ المُتغيِّراتِ	$3x + 0.67 = 1$
بطرحِ 0.67 منَ الطرفينِ	$3x = 0.33$
بقسمةِ طرفيِ المعادلةِ على 3	$\mathit{x}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{11}$