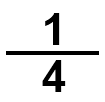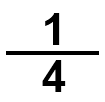الرُّبْعُ
تهيئة:
أتأمل الأشكال الآتية، ثمّ أُجيب:
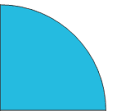
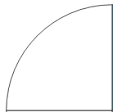
كم جُزءًا يوجد في الأشكال السابقة؟
لو قمنا بتجميع الأجزاء ما الشكل الذي سنحصل عليه؟
إلى كم جزء تمّ تقسيم الدائِرة؟
أقارن إجابتي بالإجابات الآتية:
كم جُزءًا يوجد في الأشكال السابقة؟ 4 أجزاء.
لو قمنا بتجميع الأجزاء ما الشكل الذي سنحصل عليه؟ دائِرة.
إلى كم جزء تمّ تقسيم الدائِرة؟ 4 أجزاء.
عند جمع الأجزاء السابقة فإننا نحصل على شكل الدائِرة
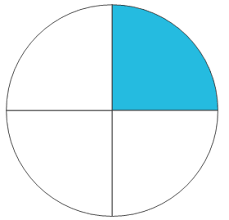
أتعلّم: يمكن تقسيم الأشكال أو الأشياء إلى أجزاء متساوية (متطابقة).
مثال: يمكنني تقسيم الدائِرة إلى أربعة أجزاء متساوية، كلُّ جزء منها يُسمى رُبْع.
قَسَّمَ رَيّانُ فَطيرَةَ الْبيتزا إِلى أَرْبَعَةِ أَجْزاءٍ مُتَطابِقَةٍ، ثُمَّ أَكَلَ أَحَدَ الَْجْزاءِ. ما الْكَسْرُ الدّالُّ عَلى الْجُزْءِ الَّذي أَكَلَهُ رَيّانُ؟
أُلاحِظُ أنّ عدد الأجزاء المتطابقة التي قُسِّمت إليها فطيرة البيتزا هي 4 أجزاء.
وأستنتج أنَّ ريّان أَكَلَ جُزءًا واحِدًا من الأجزاء الأربعة التي قُسِّمَتْ إليها فطيرة البيتزا، أيْ أنّ رَيَّان قد أَكَلَ رُبْعَ الفطيرة. وهذا الجزء يُمَثِّلُ (1) من (4).
أي أنّ عدد الأجزاء (4) وَرَيّان أَكَلَ جزءًا واحدًا (1) منها.
يُمكن تمثيل الجزء الذي أكله ريّان بالنسبة لعدد الأجزاء المتطابقة التي قُسِّمت إليها فطيرة البيتزا بما يأتي:

إِذا قَسَّمْتُ الْكُلَّ إِلى 4 أَجْزاءٍ مُتَطابِقَةٍ، فَإِنَّني أُسَمّي كُلَّ جُزْءٍ الرُّ بع (one fourth)، وَأَكْتُبُهُ
أتَأمّل المثال الآتي:
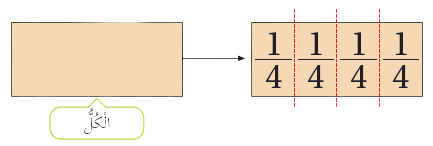
يُسَمّى كَسْرًا.
أَتَحَدَّثُ:
فيمَ يَخْتَلِفُ النِّصْفُ عَنِ الرُّبْعِ؟
أَسْتَعين في إجابتي بما يأتي:
النّصف مُقَسَّمٌ لجزأيْن متطابقين، أمّا الرّبع فمقَسَّمٌ لأربعة أجزاء مُتطابقة.