|
الشُّغلُ Work يستخدمُ الناسُ مفهومَ الشغلِ ليدلَّ على مهامَّ مختلفةٍ يقومونَ بها، وقد يختلفُ المعنى من شخصٍ إلى آخرَ، لكنَّ علماءَ الفيزياءِ يستعملونَ كلمةَ الشغلِ بمعنًى محدَّدٍ. ويبيّنُ الشكلُ (1)، أمثلةً على أنشطةٍ من الحياةِ اليوميّةِ، فأيُّها يتضمّنُ بذلَ شغلٍ بالمفهومِ العلميِّ؟
عندَما تؤثرُ قوةٌ في جسمٍ، ويتحركُ الجسمُ في أثناءِ تأثيرِ القوةِ باتجاهٍ لا يتعامدُ معَ اتجاهِها، فإنَّ القوةَ تبذلُ شغلاً على الجسمِ. وعندَما تكونُ القوةُ ثابتةً في المقدارِ والاتجاهِ، وتكونُ الحركةُ باتجاهِ تلكَ القوةِ، فإنَّ الشغلَ Work المبذولَ يُعبَّرُ عنهُ بالعلاقةِ الآتيةِ: Wf = Fd حيثُ ( F): القوةُ المؤثّرةُ، و ( d) الإزاحةُ باتجاهِ القوّةِ. والشغلُ كميّةٌ قياسيّةٌ، يُقاسُ في النظامِ العالميِّ للوَحداتِ بوَحدةِ الجولِ ورمزُها (J) .
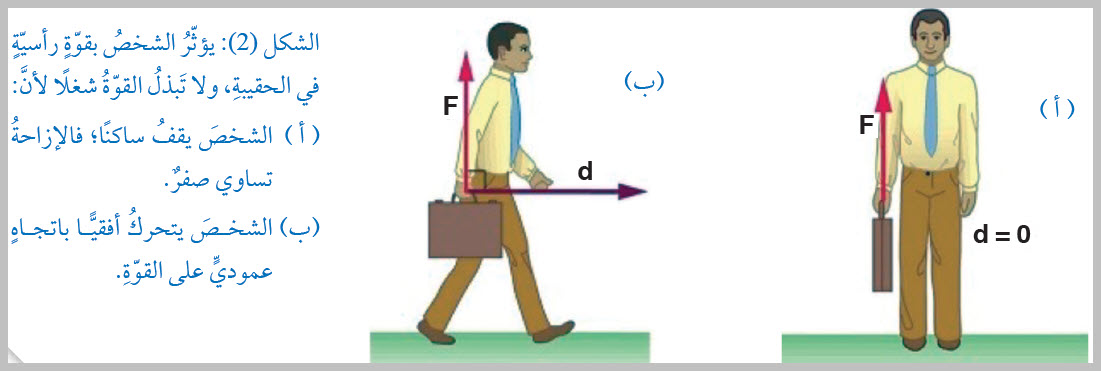
يبيّنُ الشكلُ ( 2)، حالتينِ لا تَبذلُ فيهِما القوّةُ المؤثّرةُ في الجسمِ شغلًا بالمفهومِ الفيزيائيِّ، فالشخصُ الذي يحملُ الحقيبةَ ويقفُ ساكنًا لا يبذلُ شغلً عليها؛ لأنَّهُ لا يوجدُ إزاحةٌ ( d = 0 )، الشكلُ ( 2/أ). وكذلكَ عندَما يتحركُ الشخصُ أفقيًّا، وهو يحملُ حقيبةً، على نحوِ ما هو مبيَّنٌ في الشكلِ ( 2/ب)، فإنَّ القوةَ العموديّةَ المؤثِّرةَ في الحقيبةِ لا تبذلُ شغلاً عليها؛ إذ لا توجدُ إزاحةٌ باتجاهِ القوةِ، الشكلُ ( 2/ب). |
الشكل (2) |
|
مثال محلول تؤثِّرُ فتاةٌ بقوةٍ أفقيّةٍ مقدارُها ( 60N ) في صندوقٍ، فتدفعُه على سطحٍ أفقيٍّ مسافةَ ( 5m ). أحسُبُ الشغلَ الذي بذَلَتْهُ قوّةُ الدفعِ. الحل: WF = Fd WF = 60 × 5 = 300 J |
|
|
مثال محلول يرفعُ أحمدُ صندوقًا وزنُه ( ) إلى ارتفاعِ ( ) بسرعةٍ ثابتةٍ، ثمَّ يمشي بهِ مسافةَ ( ) عبرَ الغرفةِ بسرعةٍ ثابتةٍ، فما الشغلُ المبذولُ على الصندوقِ في أثناءِ: الحلُّ: معرفةَ مقدارِ قوّةِ الرفعِ؛ وذلكَ بتطبيقِ القانونِ الثاني لنيوتن. ΣF = ma ولمّا كانتِ الحركةُ بسرعةٍ ثابتةٍ ( a = 0 )، فإذنْ: ΣF = 0 أُلاحظُ أنَّ قوّةَ الرفعِ تساوي الوزنَ؛ لأنَّ الحركةَ بسرعةٍ ثابتةٍ. ولحسابِ الشغلِ أستخدمُ العَلاقةَ: WF = F d = 40 × 1.5 = 60 J ب. في أثناءِ المشي تكونُ القوّةُ التي يؤثّرُ بها أحمدُ عموديّةً على اتجاهِ الإزاحةِ؛ فلا تَبذلُ القوّةُ شغلاً؛ .WF = 0 |
|
|
تمرين 1. أحسبُ الإزاحةَ التي يقطعُها جسمٌ عندَما تؤثّرُ فيهِ قوّةٌ مقدارُها ( 6N ) فتحرّكُّه باتجاهِها، وتبذلُ شغلاً مقدارُه ( 300J). مسافةَ (2m)، فتبذلُ عليهِ شغلاً مقدارُه (800J). |
|
|
القُدرةُ Power والتغلُّبِ على قوةِ الجاذبيّةِ الأرضيّةِ. فإذا صعِدتُ الدرجَ نفسَه بسرعةٍ ثابتةٍ أكبرَ، فإنَّني أبذلُ الشغلَ نفسَه بزمنٍ أقلَّ؛ أيْ إنَّ قُدرتي على صعودِ الدرجِ تزدادُ. تُعرَّفُ القُدرةُ Power بأنَّها المعدّلُ الزمنيُّ لبذلِ الشغلِ، وتُحسبُ بقسمةِ الشغلِ المبذولِ ( W) على الزمنِ اللازمِ لِبَذْلهِ ( t) ويُعبَّرُ عنها بالعَلاقةِ الآتيةِ:
والقدرةُ كميّةٌ قياسيٌةٌ، تُقاسُ بوحدةِ ( J/s ) وتُعرَفُ بالواط ،(Watt) ويُرمزُ إليها بالرمزِ (W). يُستخدمُ مفهومُ القدرةِ في المقارنةِ بينَ الآلاتِ؛ حيثُ تزدادُ قدرةُ الآلةِ كلَّما زادَ الشغلُ الذي تبذلُه خلالَ زمنٍ معيَّنٍ، أو عندَما تبذلُ الآلةُ الشغلَ نفسَه في زمنٍ أقلَّ. مثال محلول رافعتانِ (أ، ب) استُخدِمَتا في رفعِ جسمٍ كتلتُه ( 120kg ) إلى ارتفاعِ (15m) بسرعةٍ ثابتةٍ، والزمنُ اللازمُ لرفعِ الجسمِ باستخدامِ الرافعةِ الأولى ( 30s )، والرافعةِ الثانيةِ ( 9s ). فإذا علمتُ أنَّ تسارعَ السقوطِ الحرِّ ( 10m/s2 )، أحسبُ قدرةَ كلِّ رافعةٍ. الحلُّ: الوزنُ منَ العَلاقةِ: Fg = mg = 120 × 10 = 1200 N يُحسبُ الشغلُ اللازمُ بذلُه على الجسمِ لرفعِه، باستخدامِ العَلاقةِ: WF = F d = 1200 × 15 =18000 J ألاحظُ أنَّ الرافعتينِ تبذلانِ الشغلَ نفسَه، وأحسبُ قدرةَ كلِّ رافعةٍ باستخدامِ العَلاقةِ:
قدرةُ الرافعةِ الأولى:
قدرة الرافعة الثانية:
أُلاحظُ أنَّ قدرةَ الرافعةِ الثانيةِ أكبرُ من قدرةِ الرافعةِ الأولى، لذا فاستخدامُ الرافعةِ الثانيةِ أفضلُ منَ استخدامِ الرافعةِ الأولى؛ لأنَّها تُنجزُ الشغلَ نفسَه في زمنٍ أقلَّ. |
|
|
تمرين أحسبُ: تَرفعُ رافعةٌ جسمًا وزنُه ( 600N ) إلى ارتفاعِ ( 5m )، فيستغرقُ ذلكَ ( 1min). فما قدرةُ الرافعةِ؟ |
|
|
الشُّغلُ والطاقةُ Work and Energy درستُ في صفوفٍ سابقةٍ أنَّ للطاقةِ أشكالً مختلفةً، منها الطاقةُ الحركيّةُ،وطاقةُ الوضعِ الناشئةُ عنِ الجاذبيّةِ الأرضيّةِ، والطاقةُ الحراريةُّ... وغيرُها. وفي هذا الدرسِ سأدرسُ العَلاقةَ بينَ الشغلِ والطاقةِ الحركيّةِ. الطاقةُ الحركيّةُ Kinetic Energy طاقةً حركيّةً Kinetic Energy ، يعتمدُ مقدارُها على كلٍّ منْ: كتلةِ الجسمِ (m) وسرعتِه ( v)، ويُعبَّرُ عنها بالعَلاقةِ الآتيةِ:
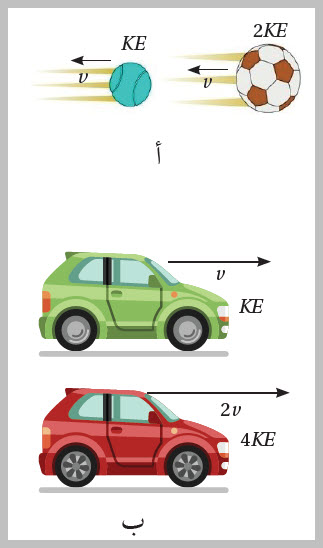
حيثُ: (KE) الطاقةُ الحركيّةُ للجسمِ، وهي كميّةٌ قياسيّةٌ، تُقاس بوَحدةِ قياسِ الشغلِ نفسِها وهيَ الجولُ (J). تُبيّنُ هذهِ العلاقةُ أنَّ الطاقةَ الحركيّةَ تتناسبُ طرديًّا معَ الكتلةِ؛ وهذا يعني أنَّ جسمًا كتلتُه ( 2m ) يمتلكُ ضِعْفي الطاقةِ الحركيّةِ التي يمتلكُها جسمٌ كتلتُه ( m) عندَما يتحركُ الجسمانِ بالسرعةِ نفسِها. أتأمّلُ الشكلَ(3/أ). كذلكَ فإنَّ الطاقةَ الحركيّةَ تتناسبُ طرديًّا معَ مربعِ السرعةِ؛ وهذا يعني أنَّ جسمًا سرعتُه () يمتلكُ أربعةَ أضعافِ الطاقةِ الحركيّةِ التي يمتلكُها جسمٌ يتحرّكُ بسرعةِ (v)، عندَما يكونُ للجسمينِ الكتلةُ نفسُها. أتأمّلُ الشكلَ (3/ب) مثال محلول تركضُ فتاةٌ كتلتُها (60kg) بسرعةِ (5m/s)، أحسبُ الطاقةَ الحركيّةَ للفتاةِ. الحلُّ:
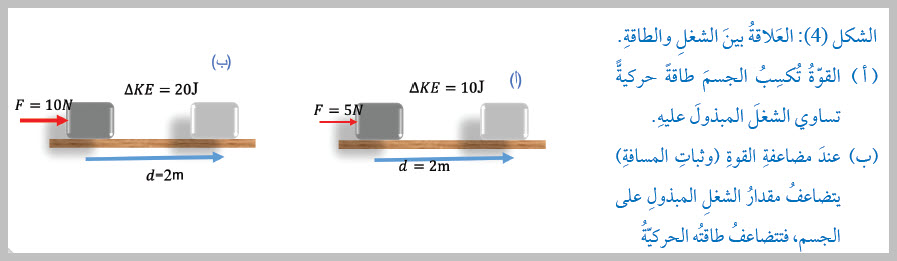
الشغلُ والطاقةُ الحركيّةُ Work and kinetic Energy عندَما تؤثّرُ قوّةٌ في جسمٍ ساكنٍ وتحرّكهُ باتجاهِها فإنَّها تبذلُ عليهِ شغلً، ولمّا كان الجسم المتحرّكُ يمتلكُ طاقةً حركيّةً، فإنَّ القوّةَ أكسبتِ الجسمَ طاقةً عندَما بذلَتْ عليهِ شغلً، لذا يُعدُّ الشغلُ وسيلةً لإكسابِ الجسمِ طاقةً حركيّةً. وللتوصّلِ إلى العلاقةِ بينّ الشغلِ والطاقةِ الحركيةِ، أتأمّلُ الشكلَ (4/أ)، الذي يبيّنُ صندوقًا تؤثّرُ فيهِ قوّةٌ ( F) فتحرّكُه إزاحةُ ( d) على سطحٍ أفقيٍّ أملسَ، فتكسبُه طاقةً حركيّةً، ونظرًا إلى أنَّ الجسمَ كانَ ساكنًا، فإنَّ طاقتَه الحركيّةَ تزدادُ، وبذلكَ فإنَّ ( ΔKE) تمثّلُ التغيُّرَ في الطاقةِ الحركيّةِ للجسمِ. وقدْ دلّتِ التجاربُ على أنَّ الشغلَ المبذولَ على الجسمِ يساوي التغيُّرَ في طاقتِه الحركيّةِ. ولمّا كانَ الشغلُ ( WF = Fd ) يتناسبُ طرديًّا معَ كلٍّ منَ القوّةِ المؤثِّرةِ والإزاحةِ، فهذا يعني أنَّ زيادةَ أيٍّ منهُما يؤدّي إلى زيادةِ الشغلِ المبذولِ على الجسمِ، فيزدادُ التغير في طاقتِه الحركيّةِ. أتأمّلُ الشكلَ (4/ب) وأُلاحظُ أنَّ ثباتَ المسافةِ التي يتحركها الجسمُ، ومضاعفةَ مقدارِ القوّةِ المؤثِّرةِ فيهِ يضاعف مقدارَ الشغلِ المبذولِ عليهِ، فيتضاعفُ مقدارُ التغيُّرِ في طاقتِه الحركيّةِ. الربط بالرياضيات معيّنةٍ، فمثلًا عندَ رصدِ الطاقةِ الحركيّةِ لجسمٍ مدةً منَ الزمنِ، فإنَّ الرمزَ (ΔKE) يعبِّرُ عنِ الفرقِ بينَ الطاقةِ الحركيّةِ النهائيّةِ والطاقةِ الحركيّةِ الابتدائيّةِ للجسمِ خلالَ تلكَ المدّةِ. الشغلُ السالبُ Negative Work في الحياةِ اليوميّةِ ألاحظُ أنَّ الأجسامَ المتحرّكةَ، مثلُ كرةِ القدمِ، تتوقّفُ عنِ الحركةِ بعدَ قطعِها مسافةً معيَّنةً على سطحٍ خشِنٍ. فما سببُ ذلكَ؟ أتأمّلُ الشكلَ ( 5). عندَما يضربُ اللاعبُ الكرةَ فإنَّه يُكسبُها طاقةً حركيّةً، وفي أثناءِ حركتِها على السطحِ الخشِنِ تؤثرُ فيها قوّةُ الاحتكاكِ، ويكونُ اتجاهُها عكسَ اتجاهِ الحركةِ. وفي هذهِ الحالةِ، تَبذلُ قوّةُ الاحتكاكِ على الكرةِ شغلً سالبًا يؤدّي إلى تناقصِ طاقتِها الحركيّةِ، وتحويلِها إلى طاقةٍ حراريّةٍ. |
الشكل ( 3): تتناسبُ الطاقةُ الحركيّةُ طرديًّا معَ:
|