رياضيات فصل أول

مفهوم أساسي :

 المتتاليةُ (Sequence): مجموعةٌ منَ الأعدادِ تَتْبَعُ ترتيبًا مُعيّنًا، ويُسمّى كلُّ عددٍ فيها حدًّا (Term) 

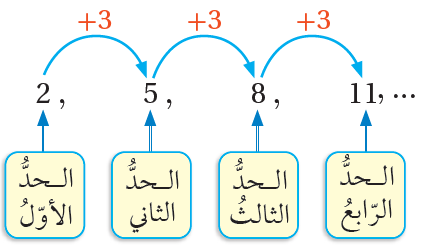
يمكنُني أنْ أكملَ حدودَ المتتاليةِ إذا علمْتُ القاعدةَ التي تربطُ كلَّ حدٍّ في المتتاليةِ بالحدِّ الذي يليهِ.

مثال 1: إذا كانَ الحدُّ الأوّلُ في متتاليةٍ هوَ 4.7 ، والقاعدةُ التي تربطُ كلَّ حدٍّ بالحَدِّ الذي يليهِ هيَ: طرحُ 0.4 ، فأجدُ الحدَّ الخامسَ.

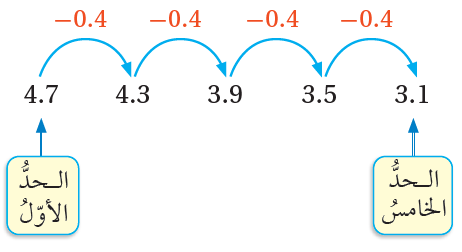
أبدأُ بالحدِّ الأوّلِ، وأطرحُ 0.4 كلَّ مرَّةٍ حتّى أصلَ إلى الحدِّ الخامسِ. إذنْ، الحدُّ الخامسُ هوَ: 3.1 

 

يمكنُني أيضًا أنْ أجدَ أيَّ حدٍّ في المُتتاليةِ إذا علمْتُ العلاقةَ التي تربطُ بينَ أيِّ حدٍّ في المتتاليةِ ورتبَتِهِ. وتُسمّى هذهِ العلاقةُ قاعدةَ الحدِّ العامِّ (n^th Term) 

يمكنُني بهذهِ الطريقةِ أنْ أجدَ الحدَّ المطلوبَ منْ دونِ الحاجةِ إلى إيجادِ جميعِ الحدودِ التي تسبقُهُ. أليسَ هذا أفضلَ؟ 

مثال 2 : إذا كانَتْ قاعدةُ الحدِّ العامِّ لمتتاليةٍ هيَ: أضربُ رتبةَ الحدِّ في 3 ثمَّ أجمعُ 2، فأجدُ كلًّ مِنَ الحدودِ: السادسِ والسابعِ والثامنِ.

رتبةُ الحدِّ السادسِ هيَ: 6، ولإيجادِ هذا الحدِّ فإنَّني أطبِّقُ قاعدةَ الحدِّ العامِّ على رتبتِهِ:

أضربُ الرتبةَ في 3، ثمَّ أجمعُ 2 معَ الناتجِ.

	الحد				الرتبة
6×3+2= 2الحدُّ السادسُ :0	20	$\stackrel{\mathbf{+}\mathbf{2}}{\mathbf{\to }}$	18	$\stackrel{\mathbf{\times }\mathbf{3}}{\mathbf{\to }}$	6
7×3+2 = الحدُّ السابعُ :23	23	$\stackrel{\mathbf{+}\mathbf{2}}{\mathbf{\to }}$	21	$\stackrel{\mathbf{\times }\mathbf{3}}{\mathbf{\to }}$	7
8×3+2 = الحدُّ الثامنُ: 26	26	$\stackrel{\mathbf{+}\mathbf{2}}{\mathbf{\to }}$	24	$\stackrel{\mathbf{\times }\mathbf{3}}{\mathbf{\to }}$	8

 

يمكنُني أنْ أجِدَ قاعدةَ الحدِّ العامِّ للمتتاليةِ بملاحظةِ القاعدةِ التي تربطُ كلَّ حدٍّ في المتتاليةِ بالحدِّ الذي يليهِ، وبملاحظةِ العلاقةِ بينَ رتبةِ كلِّ حدٍّ وقيمتِهِ.

مثال 3: في ما يأتي نَمَطٌ هندسِيُّ يشكِّلُ عددُ الدوائرِ فيهِ متتاليةً:

1) أجدُ القاعدةَ التي تربطُ كلَّ حدٍّ في المتتاليةِ بالحدِّ الذي يليهِ: 

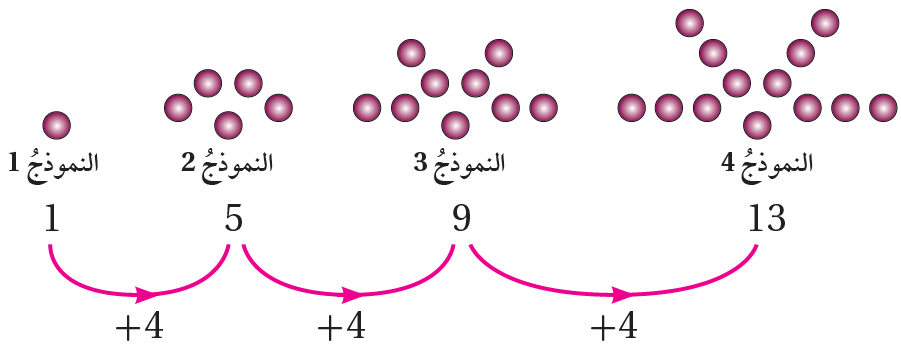
بالانتقالِ منَ الحدِّ إلى الحدِّ الذي يليهِ، أجدُ أنَّ 4 دوائرَ قدْ أُضيفَتْ. إذنْ، كلُّ . حدٍّ أكبرُ منَ الحدِّ الذي يسبِقُهُ بِ 4

2) أكتبُ قاعدةَ الحدِّ العامِّ. 

الحد				رتبة الحد
1	$\stackrel{\mathbf{-}\mathbf{3}}{\mathbf{\to }}$	4	$\stackrel{\mathbf{\times }\mathbf{4}}{\mathbf{\to }}$	1
5	$\stackrel{\mathbf{-}\mathbf{3}}{\mathbf{\to }}$	8	$\stackrel{\mathbf{\times }\mathbf{4}}{\mathbf{\to }}$	2
9	$\stackrel{\mathbf{-}\mathbf{3}}{\mathbf{\to }}$	12	$\stackrel{\mathbf{\times }\mathbf{4}}{\mathbf{\to }}$	3
13	$\stackrel{\mathbf{-}\mathbf{3}}{\mathbf{\to }}$	16	$\stackrel{\mathbf{\times }\mathbf{4}}{\mathbf{\to }}$	4

تزدادُ الحدودُ في المتتاليةِ بمقدارِ 4، وهذا يذكِّرُني بجدولِ ضربِ العددِ 4؛ إذْ إنَّ الفرقَ بينَ كلِّ ناتجَيْنِ يساوي 4، لكنَّ حدودَ المتتاليةِ أقلُّ بمقدارِ 3 منَ النواتجِ في جدولِ ضربِ العددِ 4. إذنْ،

قاعدةُ الحدِّ العامِّ هيَ: أضربُ رتبةَ الحدِّ في 4، ثمَّ أطرحُ 3

3) ما عددُ الدوائرِ في الحدِّ الذي رتبتُهُ 15 ؟

لإيجادِ عددِ الدوائرِ، فإنَّني أطبِّقُ قاعدةَ الحدِّ العامِّ على الحدِّ الذي رتبتُهُ 15 ؛ أضربُ الرتبَةَ في 4، ثمَّ أطرحُ 3 منَ الناتجِ.

الحد				الرتبة
57	$\stackrel{\mathbf{-}\mathbf{3}}{\mathbf{\to }}$	60	$\stackrel{\mathbf{\times }\mathbf{4}}{\mathbf{\to }}$	15

 

يمكنُني استعمالُ مقدارٍ جبريٍّ لكتابةِ الحدِّ العامِّ للمتتاليةِ.

مثال 4: الحدُّ العامُّ لمتتالية (أضربُ رتبةَ الحدِّ في$\frac{\mathbf{1}}{\mathbf{4}}$  ، ثمَّ أجمع $\frac{\mathbf{27}}{\mathbf{4}}$) أكتبُ الحدَّ العامَّ باستخدامِ مقدارٍ جبريٍّ، ثمَّ أستخدمُهُ  لأجدَ الحدودَ الثلاثةَ الأولى.

يمكنُني أنْ أكتبَ الحدَّ العامَّ المُعطى على صورةِ ( أي حد يساوي $\frac{1}{4}$ مضروبًا في رتبةِ الحدِّ مُضافًا إليْهِ $\frac{27}{4}$ )؛ لأرمزَ إلى رتبةِ أيِّ حدٍّ في المتتاليةِ بالمتغيّرِ n ، ولأرمزَ إلى الحدِّ نفسِهِ بالرمزِ  T_n

أكتبُ هذهِ العبارةَ بالرموزِ كما يأتي:

${\mathrm{T}}_{\mathrm{n}}=\frac{1}{4}\mathrm{n}+\frac{27}{4}$ 

أستخدمُ الحدَّ العامَّ؛ لأجدَ الحدودَ الثلاثةَ الأولى: 

قاعدة الحد العام                                     ${\mathrm{T}}_{\mathrm{n}}=\frac{1}{4}\mathrm{n}+\frac{27}{4}$                                     

أعوض رتبة الحد الأول (n=1)                ${\mathrm{T}}_{\mathbf{1}}=\frac{1}{4}\mathbf{\left(}\mathbf{1}\mathbf{\right)}+\frac{27}{4}$                                 

أبسط                                                    $$\begin{gathered} {\mathrm{T}}_{\mathbf{1}}=\frac{1}{4}+\frac{27}{4} \\ =\frac{28}{4} \\ =7 \end{gathered}$$                                 

 أعوض رتبة الحد الثاني (n=2)              ${\mathrm{T}}_{\mathbf{2}}=\frac{1}{4}\mathbf{\left(}\mathbf{2}\mathbf{\right)}+\frac{27}{4}$                               

أبسط                                                    $$\begin{gathered} {\mathrm{T}}_{\mathbf{2}}=\frac{1}{2}+\frac{27}{4} \\ =\frac{2}{4}+\frac{27}{4} \\ =\frac{29}{4} \\ =7\frac{1}{4} \end{gathered}$$                                 

أعوض رتبة الحد الثالث (n=3)              ${\mathrm{T}}_{\mathbf{3}}=\frac{1}{4}\mathbf{\left(}\mathbf{3}\mathbf{\right)}+\frac{27}{4}$                                

أبسط                                                   $$\begin{gathered} {\mathrm{T}}_{\mathbf{2}}=\frac{3}{4}+\frac{27}{4} \\ =\frac{30}{4} \\ =\frac{15}{2} \\ =7\frac{1}{2} \end{gathered}$$                               

إذنْ، الحدودُ الثلاثةُ الأولى في المتتاليةِ هيَ: $7,7\frac{1}{4},7\frac{1}{2}$