حلُّ المُعادلاتِ التربيعيَّةِ بيانِيًّا
Solving Quadratic Equations by Graphing
فكرةُ الدرسِ : حلُّ المُعادلةِ التربيعيَّةِ بيانِيًّا.
المُعادلةُ التربيعيَّةُ : مُعادلةٌ يمكنُ كتابتُها على الصورةِ : ، حيث a ≠ 0 ، والتي تُسَمّى الصورةَ القياسيَّةَ للمُعادلةِ التربيعيَّةِ، ولكلِّ
مُعادلةٍ تربيعيَّةٍ اقترانٌ تربيعيٌّ مُرتبطٌ بها يمكنُ الحصولُ عليهِ باستبدالِ (f(x بالعددِ 0.
 |
 |
يُمكن حلُّ المُعادلة التربيعيَّة بتحديد قِيَم x التي يقطعُ عندها منحنى الاقتران التربيعيِّ المُرتبط بالمُعادلة المحور x ، وَتُسَمّى تلك القِيَم جذور المُعادلة أو أصفار الاقتران.
•• يمكنُ حلُّ المُعادلة التربيعيَّة بيانيًّا باتِّباع الخُطوات الآتية :
|
مفهوم أساسيّ (حلّ المُعادلة التربيعيَّة بيانيًّا) الخطوة 1 : أكتبُ المُعادلة بالصورة القياسيَّة الخطوة 2 : أُمَثِّل بيانيًّا الاقتران التربيعيَّ المُرتبط بالمُعادلة وهو : الخطوة 3 : أجد قِيم x التي يقطع عندها منحنى الاقتران المُرتبط المحور x، إن وُجدت، وهي أصفار الاقتران المُرتبط ، التي تُعَدُّ حلولَ المُعادلة. |
أولًا : حلُّ المُعادلةِ التربيعيَّةِ بيانِيًّا : حلّانِ حقيقيانِ مختلفانِ
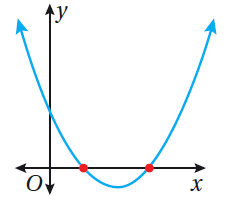 |
يكونُ للمُعادلةِ التربيعيَّةِ حلّانِ حقيقيانِ، إذا قطعَ منحنى الاقترانِ التربيعيِّ المُرتبطِ المحورَ x في نقطتَيْنِ، كما في الشكلِ المُجاورِ. |
مثال
أَحُلُّ المُعادلةَ بيانيًا.
الحل :
الخطوة 1 : أكتبُ المُعادلة بالصورة القياسيَّة، ثمَّ أكتب الاقتران التربيعيّ المُرتبط بالمُعادلة.
المُعادلةُ المُعطاةُ
بجمع 2 إلى طَرَفَيِ المُعادلةِ
إذنْ، الاقترانُ التربيعيُّ المُرتبطُ بالمُعادلةِ:
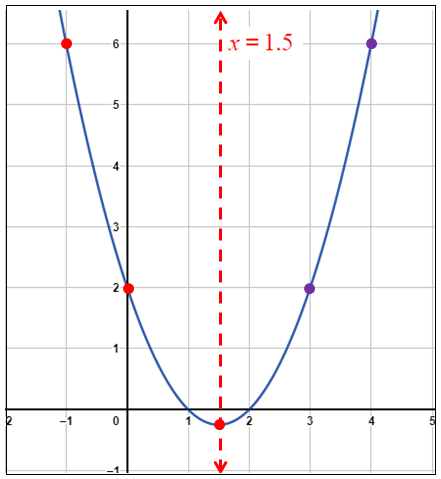 |
الخطوة 2 : أُمَثِّلُ الاقتران التربيعيّ المُرتبط بالمُعادلة بيانيًّا. • بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى. • مُعادلةُ محورِ التَّماثُلِ : x =1.5 • إحداثيّا الرأسِ : ( 0.25 - ، 1.5) • نقطةُ تقاطعِ الاقترانِ معَ المحورِ y، هِيَ : (2 , 0)، ونقطةٌ أُخرى تقعُ في الجانبِ الذي يقعُ فيهِ المقطعُ y من محورِ التماثلِ وهي مثلًا : (6 , 1-). • أُمَثِّلُ الرأسَ والنقطتَيْنِ في المُستوى الإحداثِيِّ، ثمَّ أستعملُ التَّماثُلَ لأعكِسَهُما. |
الخُطوة 3 : أَجِدُ القِيَمَ التي يقطعُ عندها المنحنى المحورَ x
يقطع المنحنى محور x عند 2 , 1 ، إذنْ : للمُعادلة جذران ، هُما : 2 , 1
ثانيًا : حلُّ المُعادلةِ التربيعيَّةِ بيانِيًّا : حلٌّ حقيقيٌّ واحدٌ.
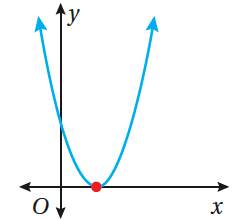 |
يكونُ للمُعادلةِ التربيعيَّةِ حلٌّ حقيقيٌّ واحدٌ إذا قطعَ منحنى الاقترانِ التربيعيِّ المُرتبطِ المحورَ x في نقطةٍ واحدةٍ فقط، كما في الشكلِ المُجاورِ. |
مثال
أَحُلُّ المُعادلةَ بيانيًا.
الحل :
الخطوة 1 : أكتبُ المُعادلةَ بالصورةِ القياسيَّةِ، ثمَّ أكتبُ الاقترانَ التربيعيَّ المُرتبطَ بالمُعادلةِ.
أُلاحِظُ أنَّ المُعادلةَ مكتوبةٌ بالصورةِ القياسيَّةِ. إذنْ، الاقترانُ التربيعيُّ المُرتبطُ بالمُعادلةِ :
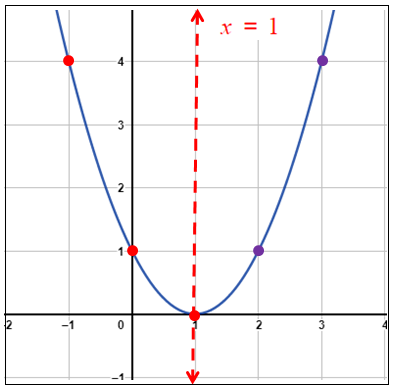 |
الخطوة 2 : أُمَثِّلُ الاقتران التربيعيّ المُرتبط بالمُعادلة بيانيًّا. • بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى. • مُعادلةُ محورِ التَّماثُلِ : x =1 • إحداثيّا الرأسِ : (0 ، 1) • نقطةُ تقاطعِ الاقترانِ معَ المحورِ y، هِيَ : (1 , 0)، ونقطةٌ أُخرى تقعُ في الجانبِ الذي يقعُ فيهِ المقطعُ y من محورِ التماثلِ وهي مثلًا : (4 , 1-). • أُمَثِّلُ الرأسَ والنقطتَيْنِ في المُستوى الإحداثِيِّ، ثمَّ أستعملُ التَّماثُلَ لأعكِسَهُما. |
الخُطوة 3 : أَجدُ القِيَم التي يقطع عندها المنحنى المحور x
يقطع المنحنى المحور x عند 1 ، إذن : للمُعادلة جذر وحيد ، هو : 1
| أتعلَّمُ : أُلاحظ أنّ الإحداثيّ x لرأس القطع هو حلُّ المُعادلة الوحيد ، عندما يكون للمعادلة حلّ واحد فقط. |
ثالثًا : حلُّ المُعادلةِ التربيعيَّةِ بيانِيًّا : لا توجدُ حلولٌ حقيقيَّةٌ.
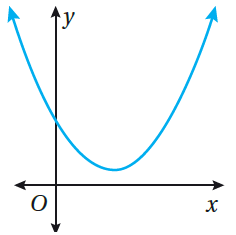 |
لا يكونُ للمُعادلة التربيعيَّة حلٌّ حقيقيّ إذا لم يقطع منحنى الاقترانِ التربيعيّ المُرتبط بالمُعادلة التربيعيَّة المحور x ، كما في الشكل المُجاور. |
مثال
أَحلّ المُعادلة بيانيًا.
الحل :
الخطوة 1 : أكتبُ المُعادلة بالصورة القياسيَّة، ثمَّ أكتب الاقتران التربيعيّ المُرتبط بالمُعادلة.
المُعادلةُ المُعطاةُ
بطرح 2 من طَرَفَيِ المُعادلةِ
إذنْ، الاقترانُ التربيعيُّ المُرتبطُ بالمُعادلةِ :
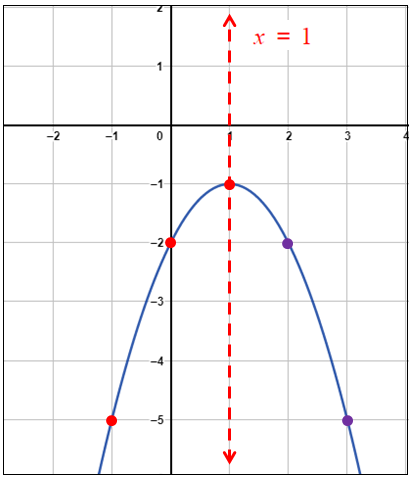 |
الخطوة 2 : أُمَثِّلُ الاقتران التربيعيّ المُرتبط بالمُعادلة بيانيًّا. • بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفل. • مُعادلةُ محورِ التَّماثُلِ : x =1 • إحداثيّا الرأسِ : (1- ، 1) • نقطةُ تقاطعِ الاقترانِ معَ المحورِ y، هِيَ : (2- , 0)، ونقطةٌ أُخرى تقعُ في الجانبِ الذي يقعُ فيهِ المقطعُ y من محورِ التماثلِ وهي مثلًا : (5- , 1-). • أُمَثِّلُ الرأسَ والنقطتَيْنِ في المُستوى الإحداثِيِّ، ثمَّ أستعملُ التَّماثُلَ لأعكِسَهُما. |
|
الخُطوة 3 : أجدُ القِيَم التي يقطع عندها المنحنى المحور x.
أُلاحظ أنَّ التمثيل البيانِيّ للاقتران المُرتبط لا يقطع المحور x ، إذنْ : لا يوجد جذر حقيقيّ للمُعادلة.
•• يأخذُ مسارُ بعضِ المقذوفاتِ شكلَ القطعِ المُكافِئِ؛ لِذا يمكنُ استعمالُ خصائصِ الاقتراناتِ التربيعيَّةِ لتحديدِ زمنِ بقاءِ المقذوفِ في الهواءِ والمسافةِ الأفقيَّةِ التي يقطعُها.
مثال من الحياة :
 |
يُمثل الاقتران h(t) = -5t2 +10t ارتفاع دولفينٍ بالمتر فوق سطح الماء بعد t ثانيةً من ظهوره فوق هذا السطح. كم ثانيةً يبقى الدولفين خارج الماء؟ |
الحل :
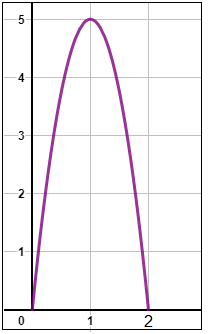 |
يكونُ ارتفاعُ الدولفين عندَ ظهوره فوق سطح الماء ، ويكونُ ارتفاعُه عندَ عودتِه إلى سطحِ الماء ؛ لِذا فإنَّ أبعدَ فترة زمنية لبقاء الدولفين فوق سطح الماء تكون عندما يقطع الاقتران h(t) = -5t2 +10t المحور x إذن ، أحلّ المُعادلة 0 = 5t2 +10t- بيانِيًّا لأحدِّد هاتين القيمتين. أُمثلُ الاقتران h(t) = -5t2 +10t بيانِيًّا ، ثم أجد القِيم التي يقطع عندها المنحنى المحور x يؤخذ من التمثيل البياني فقط الربع الأول من المستوى لأن الزمن والارتفاع لا يكون سالبًا ، وألاحظ من التمثيل أن المنحنى يقطع محور x عند 0 لحظة ظهور الدولفين على سطح الماء وعند 2 وهي لحظة عودة الدولفين إلى الماء ، إذن الفترة الزمنية التي بقي فيها الدولفين خارج الماء هي 2 ثانية .
|