حَلُّ المتباينة الخطية بمتغيرين بيانيًا
فكرة الدرس : حَلُّ متباينة خطية بمتغيرين بيانيًّا.
المتباينة الخطية : جملة رياضية تحوي الرمز ≤ ، أو ≥ ، أو > ، أو < ، وأنَّها قد تحتوي على متغير واحد أو متغيرين. من الأمثلة على المتباينات الخطية بمتغيرين:
•• يكون الزوج المُرتَّب (a , b) حلًا للمتباينة الخطية بمتغيرين إذا كان الناتج صحيحًا عند تعويض إحداثييه في المتباينة.
مثال :
أُحدِّد إذا كان كل زوج مُرتَّب ممّا يأتي يُمثل حَلًا للمتباينة :
a)
b)
الحل :
a)
نعوض الزوج المرتب في المتباينة :
| المتباينة | |
|
تعويض x = 2 ، y = -3
الناتج صحيح ، إذن الزوج المرتب (3 - ، 2) يمثل حلًا للمتباينة. |
b)
نعوض الزوج المرتب في المتباينة
| المتباينة الخطية | |
|
تعويض x = 2 ، y = -3
الناتج غير صحيح ، إذن الزوج المرتب (2 ، 1) لا يمثل حلًا للمتباينة. |
تمثيل المتباينة الخطية بمتغيرين بيانيًا ، وتحديد منطقة الحلول الممكنة لها
عند تمثيل المتباينة الخطية بيانيًّا على المستوى الإحداثي ، فإنَّ النقاط التي تُمثِّل جميع حلولها المُمكِنة تُسمّى منطقة الحلول المُمكِنة .
•• لتمثيل المتباينة بيانيًّا، أبدأ برسم مستقيم المعادلة المرافقة للمتباينة، التي أحصل عليها باستبدال الرمز ( ≥ ، ≤ ، >، <) برمز المساواة (=) ، حيث تُمثِّل المعادلة الناتجة مستقيمًا يُسمّى المستقيم الحدودي ؛ وهو مستقيم يُقسِّم المستوى الإحداثي إلى جزأين، أحدهما منطقة الحلول المُمكِنة.
قد يكون المستقيم الحدودي جزءًا من منطقة الحلول المُمكِنة إذا تضمَّنت المتباينة الرمز ≤ أو الرمز ≥ ، عندئذٍ يُرسَم المستقيم الحدودي متصلًا كما في الشكل الآتي :
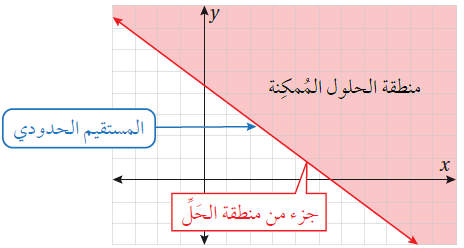
وقد لا يكون المستقيم الحدودي جزءًا من منطقة الحلول المُمكِنة إذا تضمَّنت المتباينة الرمز < أو الرمز >، عندئذٍ يُرسَم المستقيم الحدودي مُتقطِّعًا كما في الشكل الآتي :
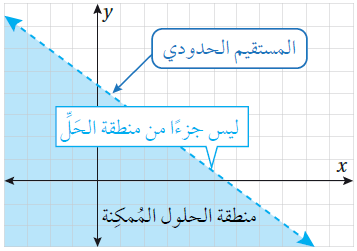
لتحديد أيِّ المنطقتين على جانبي المستقيم الحدودي هي منطقة الحلول المُمكِنة، أختار أيَّ نقطة ( a, b ) لا تقع على المستقيم الحدودي، ثم أُعوِّضها في المتباينة الخطية، فإذا كانت تُحققها (أي ينجم عنها نتيجة صحيحة) ، أُظلل الجزء من المستوى الإحداثي الذي تقع فيه تلك النقطة، وإلّا أُظلل الجزء الآخر الذي لا تقع فيه تلك النقطة.
مثال :
أُمثِّل المتباينة الخطية: x + 2y 4 على المستوى الإحداثي.
الحل :
الخطوة 1 : تمثيل المستقيم الحدودي x + 2y = 4
أُنشئ جدول قِيم لأجد نقاط تقاطع المستقيم مع المحورين ، وذلك بجعل x = 0 ؛ لأجد نقطة تقاطع المستقيم مع المحور y ، ثم جعل y = 0 ؛ لأجد نقطة تقاطع المستقيم مع المحور x
| 4 | 0 | x |
| 0 | 2 | y |
أُعيِّن النقطتين (2 , 0) و (0 , 4) على المستوى الإحداثي ، ثم أرسم مستقيمًا يمر بهما. وبما أنَّه لا توجد مساواة في رمز المتباينة فإنَّ المستقيم الحدودي يُرسم متقطعًا كما في الشكل المجاور.
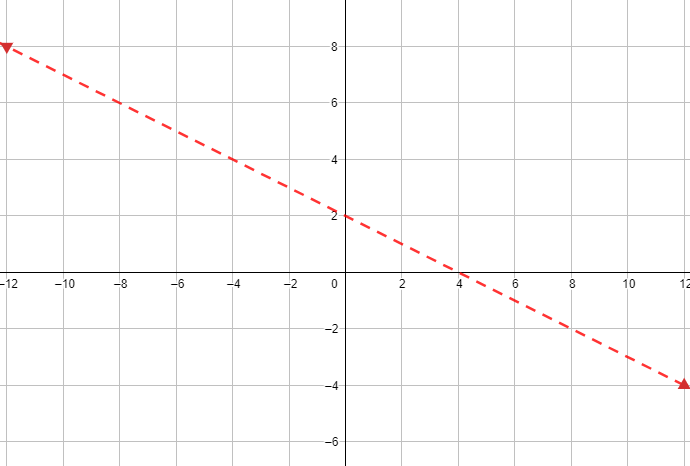
الخطوة 2 : تحديد منطقة الحلول المُمكِنة.
أختار نقطة لا تقع على المستقيم الحدودي ، مثل (0 , 0) ، ثم أتحقَّق إذا كان الناتج صحيحًا أم لا عند تعويضها في المتباينة :
المتباينة الخطية : x + 2y < 4
بالتعويض :
الخطوة 3 : تظليل منطقة الحلول المُمكِنة.
بما أنَّ النقطة ( 0 , 0) أفضت إلى ناتج صحيح للمتباينة ، فإنَّني أُظلِّل الجزء من المستوى الذي تقع فيه هذه النقطة كما في الشكل الآتي :
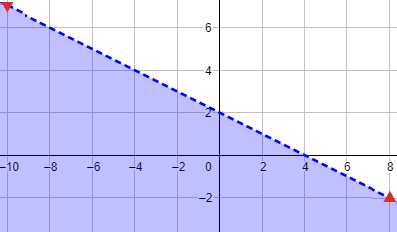
•• للمتباينات استعمالات كثيرة في المواقف العلمية والحياتية ؛ إذ تساعدنا على اتخاذ القرار الأنسب المُتعلق بتحديد القِيَم المُمكنة ضمن شروط مُحددة.
مثال :
أراد مركز تعليمي شراء نوعين من الآلات الحاسبة ، إذا كان ثمن الحاسبة من النوع الأول يساوي 15 دينار ، وثمن الحاسبة من النوع الثاني يساوي 24 دينار ، وكان المبلغ المُخصص لشراء هذه الآلات لا يزيد عن 240 دينار ، فأجد عدد الآلات الحاسبة التي يُمكن شراؤها من كل نوع.
الحل :
الخطوة 1 : أكتب المتباينة التي تعبّر عن المسألة جبريًا .
أفرض عدد الآلات الحاسبة من النوع الأول = x
أفرض عدد الآلات الحاسبة من النوع الثاني = y
الثمن = سعر القطعة الواحدة عدد القطع ، إذن ثمن النوع الأول من الحاسبات = 15x ، وثمن النوع الثاني من الحاسبات = 24y
أكوّن المتباينة :
الخطوة 2 : أمثل المتباينة
1) أرسم المستقيم الحدودي :
| 16 | 0 | x |
| 0 | 10 | y |
2) اختبار نقطة لا تقع على المستقيم الحدودي وتعويضها في المتباينة ، ثم تحديد منطقة الحل .
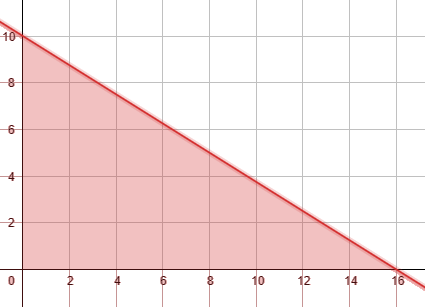
•• وهنا تنحصر منطقة الحل في الربع الأول من المستوى الإحداثي ؛ لأن أعداد الحاسبات لا يكون سالبًا ، ويُؤخذ من منطقة الحل الأعداد الصحيحة فقط لأن أعداد الحاسبات لا يكون إلا عددًا صحيحًا .
على سبيل المثال : النقطة ( 4 , 8) تُمثل حلًا للمتباينة ، ويمثل الإحدائي x عدد الحاسبات من النوع الأول ، ويمثل الإحدائي y عدد الحاسبات من النوع الثاني . وعند التعويض في المتباينة يكون الثمن أقل من 240 (أي ضمن المبلغ المُخصص لذلك).