رياضيات فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين

أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 82

أحُلُّ كُلًّ منَ المعادلاتِ الآتيةِ : 

$\mathit{a}\mathbf{)}\mathbf{ }2+\sqrt[]{x}=8$

ملاحظة : يجب التحقق من صحة الحل ، وذلك بتعويض قيمة المتغير في المعادلة الأصلية . 

$2+\sqrt[]{x}=8\to \sqrt[]{x}=6\to x=36$

$\mathit{b}\mathbf{)} 4\sqrt{7x+1}-2 = 14$

المعادلةُ الأصليةُ	$4\sqrt[]{7x+1}-2=14$
بجمع 2 إلى طرفيِ المعادلةِ	$4\sqrt[]{7x+1}=16$
بقسمة طرفي المعادلة على 4	$\sqrt[]{7x+1}=4$
بتربيع طرفي المعادلة	$7x+1=16$
بالتبسيط	$x=\frac{15}{7}$

 

$\mathit{c}\mathbf{)} 2 \sqrt[4]{x-3}=4$

المعادلةُ الأصليةُ	$2 \sqrt[4]{x-3}= 4$
بقسمة طرفي المعادلة على 2	$\sqrt[4]{x-3 }= 2$
برفع طرفي المعادلة إلى الأس الرابع	$x - 3 = 16$
بجمع 3 إلى طرفي المعادلة	$x = 19$

 

أتحقق من فهمي صفحة 83

أحُلُّ المعادلةَ : $x=\sqrt[]{x+6}$

الحل : 

المعادلةُ الأصليةُ	$x=\sqrt[]{x+6}$
بتربيع طرفي المعادلة	$x^2=x+6$
بطرح $(x+6)$ من طرفي المعادلة	$x^2-x-6=0$
بالتحليل إلى العوامل	$(x-3)(x+2)=0$
خاصيةُ الضربِ الصفريِّ	$x-3=0 or x+2=0$
بحل كل معادلة	$x=3 or x=-2$

التحقق:

عندما x = -2 

$x=\sqrt[]{x+6}$

$-2\stackrel{؟}{=}\sqrt[]{-2+6}$

$-2\ne 2 ✗$

 

عندما x = 3

$x=\sqrt[]{x+6}$

$3\stackrel{؟}{=}\sqrt[]{3+6}$

$3=3 ✓$

إذن حل المعادلة هو : $x = 3$ 

 

أتحقق من فهمي صفحة 85

أحُلُّ المعادلةَ: $\sqrt[]{3-x}=\sqrt[]{x+2}+1$

الحل : 

$\sqrt[]{3-x}=\sqrt[]{x+2}+1$	المعادلةُ الأصليةُ
$3-x=x+2+2\sqrt[]{x+2}+1$	بتربيع طرفي المعادلة
$3-x=x+2\sqrt[]{x+2}+3$	بالتبسيط
$-x= x+2\sqrt[]{x+2}$	بطرح 3 من طرفي المعادلة
$-2x= 2\sqrt{x+2}$	بطرح x من طرفي المعادلة
$-x=\sqrt[]{x+2}$	بقسمة طرفي المعادلة على 2
$x^2=x+2$	بتربيع طرفي المعادلة
$x^2-x-2=0$	بطرح (x+2) من طرفي المعادلة
$(x-2)(x+1)=0$	بالتحليل إلى العوامل
$x-2=0 or x+1=0$	خاصيةُ الضربِ الصفريِّ
$x=2 or x=-1$	بحل كل معادلة

 

التحقق:

عندما x = 2 

$\sqrt[]{3-x}=\sqrt[]{x+2}+1$

$\sqrt[]{3-2}\stackrel{؟}{=}\sqrt[]{2+2}+1$

$1\ne 3 ✗$

عندما x = - 1

$\sqrt[]{3-x}=\sqrt[]{x+2}+1$

$\sqrt[]{3-(-1)}\stackrel{؟}{=}\sqrt[]{(-1)+2}+1$

$2=2 ✓$

إذن حل المعادلة هو : $x = -1$

---

أتحقق من فهمي صفحة 86

مُعتمِدًا المعادلةَ في المثالِ 4، أجدُ طولَ البندولِ إذا تحرَّكَ حركةً تذبذبيةً مَرَّةً واحدةً ذهابًا وإيابًا في 8 ثوانٍ، مُقرِّبًا إجابتي إلى أقربِ

منزلةٍ عشريةٍ واحدةٍ.

الحل : 

المعادلة في المثال :  $T=2\mathrm{\pi } \sqrt[]{\frac{\mathrm{L}}{32}}$ 

حيث T الزمن بالثواني الذي يستغرقُهُ بندولٌ طولُهُ L قدمًا حتّى يتحرَّكَ حركةً تذبذبيةً مَرَّةً واحدةً ذهابًا وإيابًا.

المعادلةُ الأصليةُ	$T=2\mathrm{\pi } \sqrt[]{\frac{\mathrm{L}}{32}}$
بتعويض T = 8	$8=2\mathrm{\pi } \sqrt[]{\frac{\mathrm{L}}{32}}$
بقسمةِ طرفيِ المعادلةِ على  $2\mathrm{\pi }$	$\frac{8}{2\mathrm{\pi }}= \sqrt[]{\frac{\mathrm{L}}{32}}$
بالتبسيطِ	$\frac{4}{\mathrm{\pi }}=\sqrt[]{\frac{\mathrm{L}}{32}}$
بتربيعِ طرفيِ المعادلةِ	$\frac{16}{{\mathrm{\pi }}^2}=\frac{L}{32}$
بضربِ طرفيِ المعادلةِ في 32	$\frac{512}{{\mathrm{\pi }}^2}=L$
باستخدام الآلةِ الحاسبةِ	$L\approx 51.9$

 

أتحقَّقُ : للتحقُّقِ منْ صحَّةِ الحَلِّ، أُعوِّضُ قيمةَ L الناتجةَ في المعادلةِ الأصليةِ.

المعادلةُ الأصليةُ	$T=2\mathrm{\pi } \sqrt[]{\frac{\mathrm{L}}{32}}$
بتعويض $T=8, L\approx 51.9$	$8\stackrel{؟}{\approx }2\mathrm{\pi } \sqrt[]{\frac{51.9}{32}}$
باستخدام الآلةِ الحاسبةِ	$8\approx 8 ✓$

 

أسئلة أتدرب وأحل المسائل

أحُلُّ كُلًّ منَ المعادلاتِ الآتيةِ:

$\mathbf{1}\mathbf{)} \sqrt[]{3x}-5=7$

$\sqrt[]{3x}=12\to 3x=144\to x=48$

---

$\mathbf{2}\mathbf{)}\mathbf{ }\sqrt[3]{1-2x}=-3$

$1-2x =-27\to -2x=-28\to x=14$

---

$\mathbf{3}\mathbf{)} \sqrt[4]{4x+1}=2$

${\left(\sqrt[4]{4x+1}\right)}^4=2^4$

$4x +1=16\to 4x=15\to x=\frac{15}{4}$

---

$\mathbf{4}\mathbf{)} 6-\sqrt[]{y-5}=3$

$-\sqrt[]{y-5}=-3\to \sqrt[]{y-5}=3\to y-5=9\to y=14$

---

$\mathbf{5}\mathbf{)}\mathbf{ }\sqrt[]{2-x}+3=x+7$                              

$\sqrt[]{2-x}=x+4$

${\left(\sqrt[]{2-x}\right)}^2={(x+4)}^{2}2-x= x^2+8x+16$

$x^2+9x+14=0$

$(x+2)(x+7)=0$

$x=-2 or x=-7$                                                      

$x=-2 :\mathrm{التحقق} \mathrm{بعد}$

---

$\mathbf{6}\mathbf{)}\mathbf{ }\sqrt[]{5x+4}=3\sqrt[]{x}$

$5x+4=9x\to 4=4x\to x=1$

---

$\mathbf{7}\mathbf{)} \sqrt[]{2p+3}=\sqrt[]{5p-3}$

$2p+3=5p-3\to -3p=-6\to p=2$

---

$\mathbf{8}\mathbf{)}\mathbf{ }\sqrt[]{4x-1}-4\sqrt[]{2-5x}=0$

$\sqrt[]{4x-1}=4 \sqrt[]{2-5x}$

$4x-1=16(2-5x)$

$4x-1=32-80x$

$84x=33\to x=\frac{33}{84}$

---

$\mathbf{9}\mathbf{)} \sqrt[3]{1-3x}+5=3$

$\sqrt[3]{1-3x}=-2$

$1-3x=-8\to -3x=-9\to x=3$

---

$\mathbf{10}\mathbf{)}\mathbf{ }12+\sqrt[]{2v-1}=4$

$\sqrt[]{2v-1}=-8$

 بما أنّ الجذر التربيعي يساوي عددًا سالبًا ؛ إذن لا يوجد حلول لهذه المعادلة .

---

$\mathbf{11}\mathbf{)} \sqrt[]{45-6n}=n-3$                              

$45-6n=n^2-6n+9$

$n^2-36=0\to n^2=36$

$n=6 or n=-6$

$n= 6 : \mathrm{التحقق} \mathrm{بعد}$

---

$\mathbf{12}\mathbf{)}\mathbf{ }\sqrt[]{4k-4}=k-1$                                                                          

$4k-4=k^2-2k+1$

$k^2-6k+5=0$

$(k-5)(k-1)=0$

$k=5 or k=1$

$k=5 :\mathrm{التحقق} \mathrm{بعد}$

 

$\mathbf{13}\mathbf{)}\mathbf{ }\sqrt[]{x+1}=2-\sqrt[]{x}$

$x+1=4 -4\sqrt[]{x}+ x$

$-4\sqrt[]{x}=-3\to \sqrt[]{x}= \frac{3}{4}\to x=\frac{9}{16}$

 

$\mathbf{14}\mathbf{)} r+4=\sqrt[]{-4r-19}$

$r^2+8r+16=-4r-19$

$r^2+12r+35=0$

$(r+5)(r+7)=0$

$r=-5 or r=-7$

بعد التحقق بتعويض قيم r في المعادلة الأصلية ، لا يوجد حل لهذه المعادلة . 

 

$\mathbf{15}\mathbf{)} \sqrt[3]{7y-2}=\sqrt[3]{y+4}$

$7y-2=y+4\to 6y=6\to y=1$

 

$\mathbf{16}\mathbf{)}\mathbf{ }\sqrt[]{5m-16}=m-2$

$5m-16=m^2-4m+4$

$m^2-9m+20=0$

$(m-4)(m-5)=0$

$m=4 or m=5$

بعد التحقق بتعويض قيم m في المعادلة الأصلية ، أجد أنّ للمعادلة حلان هما m = 4 ، m = 5 . 

 

$\mathbf{17}\mathbf{)}\mathbf{ }\sqrt[]{9x^2+4x-4}=3x$

$9x^2+4x-4=9x^2$

$4x-4=0\to 4x=4\to x=1$

 

$\mathbf{18}\mathbf{)}\mathbf{ }\sqrt[]{x^2+5x}=\sqrt[]{6}$

$x^2+5x=6$

$x^2+5x-6=0$

$(x+6)(x-1)=0$

$x=-6 or x=1$

بعد التحقق بتعويض قيم x في المعادلة الأصلية ، أجد أنّ للمعادلة حلان هما $x=-6، x=1$ . 

---

يُبيِّنُ الشكلُ المُجاوِرُ التمثيلَ البيانيَّ لمنحنى كلٍّ منَ المعادلةِ: $y=\sqrt[]{x+3}$ ، والمعادلةِ: $y=\sqrt[]{2x+2}$:

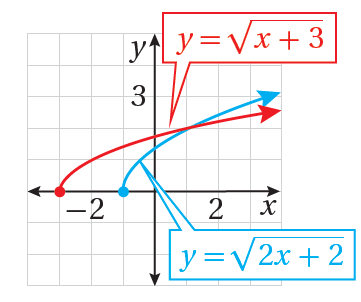
19) أكتبُ معادلةً حَلُّها هوَ الإحداثيُّ x لنقطةِ تقاطعِ منحنييِ المعادلتينِ.

الحل: 

$\sqrt[]{x+2}=\sqrt[]{-x+4}$

 

20) أحُلُّ المعادلةَ التي كتبْتُها في الفرعِ السابقِ جبريًّا.

الحل : 

$\sqrt[]{x+2}= \sqrt[]{-x+4}$

$x+2=-x+4$

$2x=2\to x=1$

 

21) إذا كانَ محيطُ المستطيلِ المُجاوِرِ هوَ $22 cm$ ، فأجدُ قيمةَ $x$.

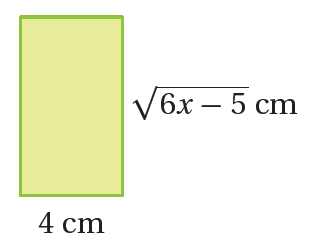
الحل : 

$22=2\times 4+2\left(\sqrt[]{6x-5}\right)$

$22=8+2\left(\sqrt[]{6x-5}\right)$

$14=2\left(\sqrt[]{6x-5}\right)$

$\Rightarrow \sqrt[]{6x-5}=7$

$6x-5=49$

$6x=54\to x=9$

 

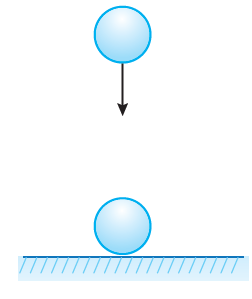22) فيزياءُ: تعطى سرعةُ الجسمِ الساقطِ سقوطًا حُرًّا منَ ارتفاعٍ قدرُهُ d قدمًا عندَ وصولِهِ سطحَ الأرضِ بالمعادلةِ الآتيةِ : $v=\sqrt[]{64 d}$  ، حيثُ $v$ سرعةُ الجسمِ بالقدمِ لكلِّ ثانيةٍ. أجدُ الارتفاعَ الذي سقطَ منْهُ الجسمُ إذا كانَتْ سرعتُهُ عندَ وصولِهَ سطحَ الأرضِ هيَ $150 \mathrm{ft}/\mathrm{s}$

الحل : 

$v=\sqrt[]{64d}$

$150=\sqrt[]{64d}$

$22500=64d$

$\Rightarrow d=\frac{22500}{64}\approx 351.5625 ft$

 

23) أحُلُّ المسألةَ الواردةَ بدايةَ الدرسِ.

مسألةُ اليومِ : تعطى سرعةُ الصوتِ بالمترِ لكلِّ ثانيةٍ قربَ سطحِ الأرضِ بالمعادلةِ الآتيةِ: $V=20\sqrt[]{t+273}$ ، حيثُ t درجةُ الحرارةِ بالسلسيوس. إذا كانَتْ سرعةُ الصوتِ هيَ $340 m/s$ ، فما درجةُ الحرارةِ عندئذٍ؟

الحل : 

$V=20 \sqrt[]{t+273}$

$340=20 \sqrt[]{t+273}$

$17=\sqrt[]{t+273}$

$289=t+273\Rightarrow t=16s$

---

أسئلة مهارات التفكير العُليا

24) أكتشفُ المختلفَ: أيُّ المعادلاتِ الآتيةِ مختلفةٌ، مُبرِّرًا إجابتي؟

الحل : 

المعادلة المختلفة : $\sqrt[]{x+1}+5=2$

لأنّ جميع المعادلات لها حلول باستثناء المعادلة  $\sqrt[]{x+1}+5=2$ ليس لها حل. 

 

25) أكتشفُ الخطأَ: حَلَّتْ بيانُ المعادلةَ: $x=\sqrt[]{12-4x}$ على النحوِ الآتي، قائلةً إنَّ للمعادلةِ حَلَّينِ اثنينِ، هما: $x=2$ و $x=-6$:

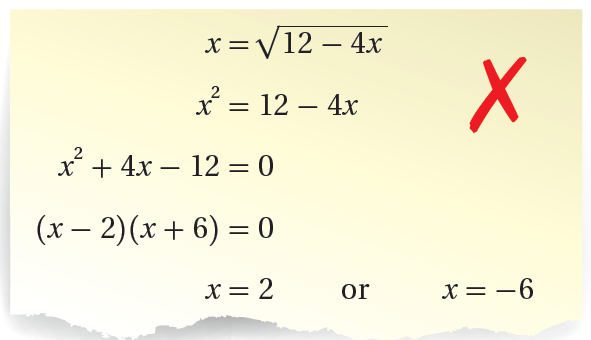
أكتشفُ الخطأَ في قولِ بيانَ، ثمَّ أُصحِّحُهُ.

الإجابة : الخطأ في عدم التحقق من صحة الحل ، وذلك بتعويض قيم x في المعادلة الأصلية .

التحقق : 

إذن حل المعادلة هو :  $x = 2$

 

26) مسألةٌ مفتوحةٌ: أكتبُ معادلةً جذريةً حَلُّها هوَ : $x = 6$

الحل : 

$\sqrt[]{3x+7}=5$

$3x+7=25\to 3x=18\to x=6$

---

أسئلة كتاب التمارين

أحُلُّ كُلًّ منَ المعادلاتِ الآتيةِ :

ملاحظة : يجب التحقق من الحل ، وذلك بتعويض قيمة المتغير في المعادلة الأصلية . 

$\mathbf{1}\mathbf{)}\mathbf{ }\sqrt[]{3r+2}=2\sqrt[]{r}$

$3r+2=4r\to r = 2$

 

$\mathbf{2}\mathbf{)} \sqrt[]{3b-2}+19=24$

$\sqrt[]{3b-2}=5\to 3b-2=25\to b=9$

 

$\mathbf{3}\mathbf{)} \sqrt[]{26-n}=7$

$26-n=49\to n=-23$

 

$\mathbf{4}\mathbf{)} \sqrt[]{2x}=\sqrt[]{x+7}-1$

$2x=x+7-2\sqrt[]{x+7}+1$

$x-8=-2\sqrt[]{x+7}$

$x^2-16x+64=4x+28$

$x^2-20x+36=0$

$(x-18)(x-2)=0$

$x=18 or x=2$

بعد التحقق : $x = 2$  

 

$\mathbf{5}\mathbf{)}\mathbf{ }2x=\sqrt[]{4x^2+6x-12}$

$4x^2=4x^2+6x-12$

$-6x=-12\to x=2$

 

$\mathbf{6}\mathbf{)} \sqrt[]{x-2}+\sqrt[]{x-13}=11$

$\sqrt[]{x-2}=11-\sqrt[]{x-13}$

$x-2=121 -22\sqrt[]{x-13}+ x-13$

$22\sqrt[]{x-13}=110$

$\sqrt[]{x-13}=\frac{110}{22}$

$\sqrt[]{x-13}=5$

$x-13=25\to x=38$

 

$\mathbf{7}\mathbf{)}\mathbf{ }\sqrt[]{x-2}-\sqrt[]{x+2}+2=0$

$\sqrt[]{x-2}=\sqrt[]{x+2}-2$

$x-2=x+2-4\sqrt[]{x+2}+4$

$-4\sqrt[]{x+2}=-4$

$\sqrt[]{x+2}=1\to x+2=1\to x=-1$

بعد التحقق بتعويض x = - 1 في المعادلة الأصلية فإنها لا تحقق المعادلة ؛ إذن المعادلة ليس لها حل . 

 

$\mathbf{8}\mathbf{)} \sqrt[4]{2x-9}=3$

$2x-9=81\to 2x=90\to x=45$

 

$\mathbf{9}\mathbf{)} \sqrt[3]{2x+4}-2=0$

$\sqrt[3]{2x+4}=2$

$2x+4=8\to 2x=4\to x=2$

 

$\mathbf{10}\mathbf{)} 3\sqrt{x-2}+2=x$

$3\sqrt[]{x-2}=x-2$

$9(x-2)=x^2-4x+4$

$9x-18=x^2-4x+4$

$x^2-13x+22=0$

$(x-11)(x-2)=0$

$x=11 or x=2$

بعد التحقق من صحة الحل ألاحظ أنّ x = 11 ، x = 2 تحققان المعادلة الأصلية. 

 

$\mathbf{11}\mathbf{)} -10\sqrt[]{v-10}=-60$

$\sqrt[]{v-10}=6\to v-10=36\to v=46$

 

$\mathbf{12}\mathbf{)} \sqrt[]{2n-88}= \sqrt[]{\frac{n}{6}}$

$2n-88=\frac{n}{6}$

$12n-528=n\to 11n=528\to n=48$

 

$\mathbf{13}\mathbf{)}\mathbf{ }2x=\sqrt[]{17x-15}$

$4x^2=17x-15$

$4x^2-17x+15=0$

أستخدم القانون العام لحل المعادلة

$x=\frac{-b\pm \sqrt[]{b^2-4ac}}{2a}=\frac{-(-17)\pm \sqrt[]{{17}^2-4\left(4\right)\left(15\right)}}{2\left(4\right)}$

$x=\frac{17\pm \sqrt[]{49}}{8 }$

$x=\frac{17+7}{8} or x=\frac{17-7}{8}$

$x=3 or x=1.25$

بعد التحقق من صحة الحل ألاحظ أنّ x = 1.25 ، x = 3 تحققان المعادلة الأصلية. 

---

 

$\mathbf{14}\mathbf{)} r+4=\sqrt[]{-4r-11}$

$r^2+8r+16=-4r-11$

${\mathrm{r}}^2+12\mathrm{r}+27=0$

$(\mathrm{r}+9)(\mathrm{r}+3)=0$

$\mathrm{r}=-9 \mathrm{or} \mathrm{r}=-3$

بعد التحقق من صحة الحل ألاحظ أنّ  r = -3 تحقق المعادلة الأصلية.

---

 

$\mathbf{15}\mathbf{)} -3g=\sqrt[]{-18-27g}$

$9g^2=-18-27g$

$9g^2+27g+18=0$

$g^2+3g+2=0$

$(g+2)(g+1)=0$

$g=-2 or g=-1$

بعد التحقق من صحة الحل ألاحظ أنّ  g = -1 ، g = -2 تحققان المعادلة الأصلية.

 

16) إذا كانَتْ مساحةُ المُثلَّثِ المُجاوِرِ هيَ $\sqrt[]{5x-4} c{m}^2$ ، فأجدُ  قيمةَ x

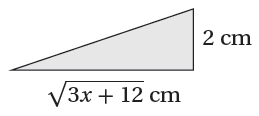الحل : 

$\sqrt[]{5x-4}=\frac{1}{2}\times \sqrt[]{3x+12}\times 2$

$\sqrt[]{5x-4}=\sqrt[]{ 3x+12}$

$5x-4=3x+12$

$2x=16\to x=8$

 

يُبيِّنُ الشكلُ المُجاوِرُ التمثيلَ البيانيَّ لمنحنى كلٍّ منَ المعادلةِ : $y=\sqrt[]{3x+7}$ والمعادلةِ : $y=\sqrt[]{x+5}$    17) أكتبُ معادلةً حلُّها هوَ الإحداثيُّ x لنقطةِ تقاطعِ منحنييِ المعادلتينِ. 18) أحُلُّ المعادلةَ التي كتبْتُها في الفرعِ السابقِ جبريًّا.

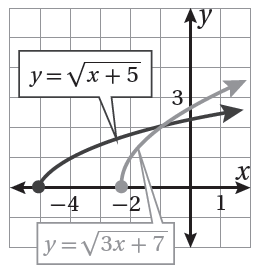الحل : 

17)

$\sqrt[]{4x+8}=2$

18)

$\sqrt[]{4x+8}=2$

$4x+8=4\to x=-1$

 

19) أكتشفُ الخطأَ : أكتشفُ الخطأَ في الحَلِّ المُجاوِرِ، ثمَّ أُصحِّحُهُ.

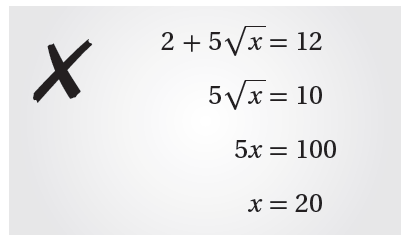
الإجابة: 

الخطأ في عدم تربيع معامل $\sqrt[]{x}$

الحل الصحيح: 

$2+5\sqrt[]{x}=12$

$5\sqrt[]{x}=10\to 25x=100\to x=4$

---