رياضيات فصل أول

مفهوم أساسي:

يُشكِّلُ كلُّ ضِلْعينِ في مثلّثٍ زاويةً داخليةً (Interior angle) ومجموعُ قياساتِ هذهِ الزوايا الداخليةِ الثلاثِ يساوي$\mathbf{180}\mathbf{°}$؛ أتحقّقُ منْ ذلكَ باستعمالِ ما تعلَّمْتُهُ عنِ الزوايا الناتجةِ منْ تقاطعِ مستقيمٍ معَ مستقيمينِ متوازيينِ.

عندَ رَسْمِ المستقيمِ $\overleftrightarrow{\mathbf{A}\mathbf{R}}$ الذي يوازي ضلعَ المثلّثِ $\overline{\mathbf{C}\mathbf{B}}$ نلاحظُ ما يأتي:

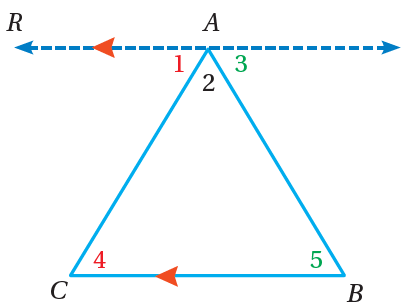
زاويتانِ متبادلتانِ داخليًّا                                                  $\mathrm{m}\angle 1= \mathrm{m}\angle 4$                                                              

زاويتانِ متبادلتانِ داخليًّا                                                  $\mathrm{m}\angle 3= \mathrm{m}\angle 5$                                                              

زوايا متجاورةٌ على مستقيمٍ                                            $\mathrm{m}\angle 1+ \mathrm{m}\angle 2+ \mathrm{m}\angle 3 =180°$                                    

أُعوِّضُ عنِ الزاويةِ   $\text{m∠5 بـ m∠3 و m∠4 بـ m∠1}$          $\mathrm{m}\angle 4+ \mathrm{m}\angle 2+ \mathrm{m}\angle 5 =180°$                                  

إذنْ، مجموعُ قياساتِ زوايا المثلثِ الداخليّةِ هوَ °180

 

يمكنُ استخدامُ العلاقةِ بينَ مجموعِ قياساتِ زوايا المثلثِ لإيجادِ قياساتِ زوايا مجهولةٍ.

مثال1: معتمدًا الشكلَ المجاورَ، أجدُ كلٍّ ممّا يأتي:

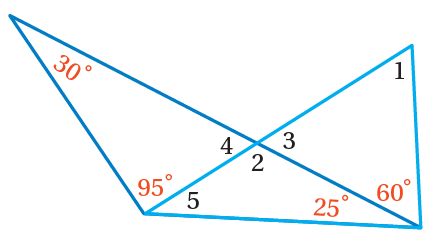
1) $\mathbf{m}\mathbf{\angle }\mathbf{4}$

مجموع زوايا المثلث الداخلية                                 $30°+95°+ \mathrm{m}\angle 4 =180°$                                          

أجد الناتج                                                                $$\begin{gathered} 125°+\mathrm{m}\angle 4 =180° \\ \mathrm{m}\angle 4 =55° \end{gathered}$$                                                  

2) $\mathbf{m}\mathbf{\angle }\mathbf{2}$

زاويتان متجاورتان على مستقيمٍ                                  $\mathrm{m}\angle 2 + \mathrm{m}\angle 4 =180°$                                               

أجد الناتج                                                                      $$\begin{gathered} \mathrm{m}\angle 2 + 55°=180° \\ \mathrm{m}\angle 2 =125° \end{gathered}$$                                                  

 

مفهوم أساسي:

الزاويةُ الخارجيّةُ للمثلث (Exterior angle): هيَ الزاويةُ الّتي تتشكَّلُ منْ أحدِ أضلاعِ المثلّثِ وامتدادِ الضّلعِ المجاورِ له، وقياسُ أيِّ زاويةٍ خارجيةٍ في المثلثِ يساوي مجموعَ قياسَيِ الزاويتينِ الداخليتَيْنِ البعيدَتَيْنِ. 

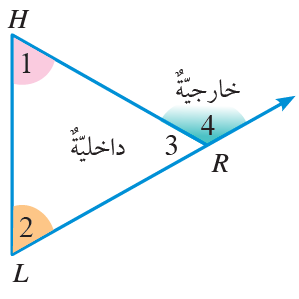
في الرسمِ المجاورِ،$\angle 4$خارجيةٌ للمثلثِ؛ ولذلكَ $\mathrm{m}\angle 4 = \mathrm{m}\angle 1+\mathrm{m}\angle 2$

أتحقَّقُ منْ ذلكَ عنْ طريقِ ما تعلَّمْتُهُ عنْ حقائقِ الزوايا

:△HRL في المثلّثِ

زوايا داخليةٌ في مثلثٍ                                                                       $\mathrm{m}\angle 1+ \mathrm{m}\angle 2+ \mathrm{m}\angle 3 =180°$                                  

زاويتانِ متجاورتانِ على مستقيمٍ                                                      $\mathrm{m}\angle 4+\mathrm{m}\angle 3=180°$                                                

أعوض                                                                     $\mathrm{m}\angle 4+\mathrm{m}\angle 3=\mathrm{m}\angle 1+\mathrm{m}\angle 2+\mathrm{m}\angle 3$                       

أطرحُ $\text{m∠3}$ من الطرفين                                                     $\mathrm{m}\angle 4=\mathrm{m}\angle 1+\mathrm{m}\angle 2$                                                  

 

يمكنُني استخدامُ خاصيةِ الزاويةِ الخارجيةِ للمثلثِ لإيجادِ قياساتِ زوايا مجهولةٍ.

مثال 2: منَ الحياةِ : أرجوحةٌ: تُشكِّلُ دعاماتُ أرجوحةٍ مُثلَّثًا كما في الشكلِ المجاورِ، أجدُ قياسَ كلٍّ منَ الزوايا الآتيةِ معتمِدًا الشكلَ:

1) $\mathbf{\text{m∠2}}$

زاويةٌ خارجيةٌ للمثلثِ                            $110°=60°+\mathrm{m}\angle 2$                                                  

   أطرحُ °60 منَ الطرفينِ                                 $\mathrm{m}\angle 2=50°$                                                         

2) $\mathbf{\text{m∠1}}$

 زوايا داخليةٌ في مثلثٍ                                    $\mathrm{m}\angle 1+\mathrm{m}\angle 2+ 60°=180°$                                   

أعوض $\text{m∠2}$                                                  $\mathrm{m}\angle 1+50°+60°=180°$                                        

أجد الناتج                                                       $$\begin{gathered} \mathrm{m}\angle 1+110°=180° \\ \mathrm{m}\angle 1=70° \end{gathered}$$