مِساحَةُ الْمُثَلَّثِ

فِكرةُ الدَّرس: أَحسُبُ مِساحَةَ الْمُثَلَّثِ.

 

يبين الشكل مجموعة من المثلثات حَيثُ قاعِدَةُ المُثَلَّثِ (b) هِيَ أَحَدُ أَضلاعِ المثلث ، وارتِفاعُهُ (h) هُوَ (المسافَةُ العموديَّةُ بَين القاعدة أَو امتِدادُها وَالرَّأْسِ الْمُقابِلِ لَها)

مَفْهومٌ أَساسِيٌّ: مِساحَةُ الْمُثَلَّثِ

بِالكَلِماتِ: مساحَةُ المُثَلَّث (A) تُساوي نِصفَ حاصِلِ ضَربِ طول القاعدَة في الارتفاعِ.

بالرُّموزِ: $\mathbf{A}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{\times }\mathit{b}\mathbf{\times }\mathit{h}$

• حَيثُ A مساحَةُ المثلث ، b طولُ قاعِدَتِهِ، h ارْتِفاعُهُ.

مثال:

أَجِدُ مِساحَةَ الْمُثَلَّثِ في كُلٍّ مِمّا يَأْتي:

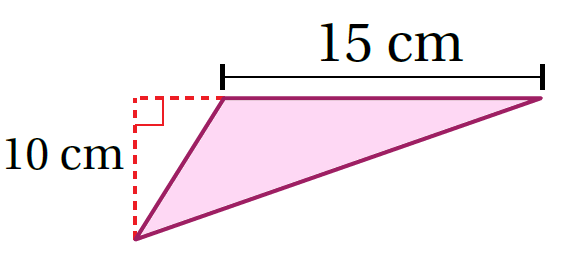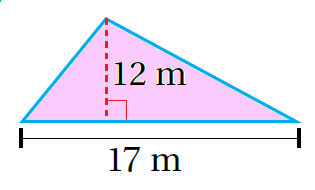صيغة مساحة المثلث:                   $\mathrm{A}=\frac{1}{2}\times b\times h$	صيغة مساحة المثلث:                    $\mathrm{A}=\frac{1}{2}\times b\times h$
$\mathrm{A}=\frac{1}{2}\times 15\times 10 , b=15 cm , h=10 cm$	$\mathrm{A}=\frac{1}{2}\times 17\times 12 , b=17 m , h=12 m$
$\mathrm{A}=75 {\mathrm{cm}}^2$	$\mathrm{A}=102 m^2$

 

 

 

 

 

 

 

 

 

---

يُرسمُ المُثلّثُ أحيانًا على شبكة المُربّعات، وعندئذ يُمكنُ تحديدُ طول قاعدته وارتفاعه بعدّ المُربّعات، وتكونُ المساحةُ بالوحدة المُربّعة.

مثال:

أجدُ مساحة المُثلّث في الشبكة الآتية:

 

 

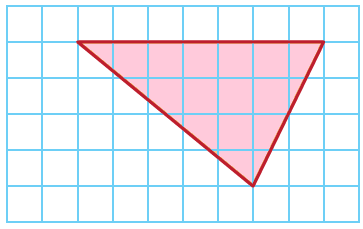الجواب

أبدأُ بعدّ الوحدات الأفُقيّة لجد طول قاعدة المُثلّث، ثُمّ أعُدُّ الوحدات الرّأسيّة لأجد ارتفاعهُ. أُلاحظُ أنّ b تُساوي 7 وحدات ، و h تُساوي 4 وحدات.

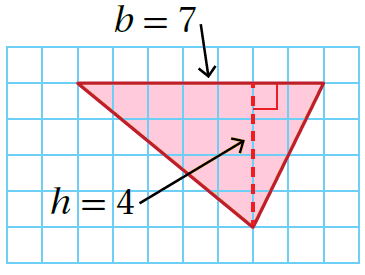صيغة مساحة المثلث:                               $\mathrm{A}=\frac{1}{2}\times b\times h$

$\mathrm{A} =\frac{1}{2}\times 7 \times 4 \mathrm{b}=\mathrm{وحدات} 7 , \mathrm{h}=\mathrm{وحدات} 4$

$\mathrm{A}= \mathrm{مُربعة} \mathrm{وحدة} 14$

 

---

يُمكنُ إيجادُ طول قاعدة المُثلّث أو ارتفاعه إذا عُلمت مساحتُهُ، وذلك باستخدام العلاقة بين عمليّتي الضّرب والقسمة.

مثال:

أَجِدُ طول القاعدَة b أَو الارتفاعَ h المَجهول في كُلِّ مُثلّثٍ ممّا يَأتي:

2) A= 2.7 cm2	1) A = 25 m2
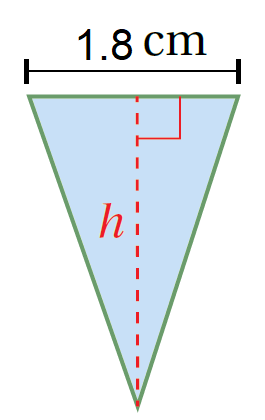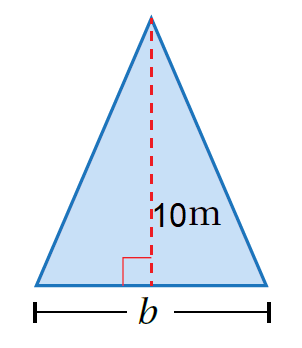صيغة مساحة المثلث:  $\mathrm{A}=\frac{1}{2}\times b\times h$	صيغة مساحة المثلث:  $\mathrm{A}=\frac{1}{2}\times b\times h$
$2.7=\frac{1}{2}\times 1.8\times h b=1.8 cm , h= ? cm , \mathrm{A}=2.7 c{m}^2$	$25=\frac{1}{2}\times b\times 10 b=? m , h= 10m , \mathrm{A}=25 m^2$
$2.7=0.9\times h \to h=3 cm$	$25=b\times 5 \to b=5 m$

 

---

تُستخدمُ صيغةُ مساحة المُثلّث والمُضلّعات الّتي تعلّمتُها سابقًا في كثير من المواقف الحياتيّة.

مثال يبين الشكل قطعة أرض مُحدّدة بجدولي ماء . ما مساحة هذه القطعة. الجواب أُقسّمُ الشّكل إلى مُضلّعات يُمكنُ إيجادُ مساحة كُلّ منها بسُهولة. يُمكنُ تقسيمُ الشّكل إلى مُستطيل ومُثلّث كما يظهرُ في الشّكل أدناهُ.

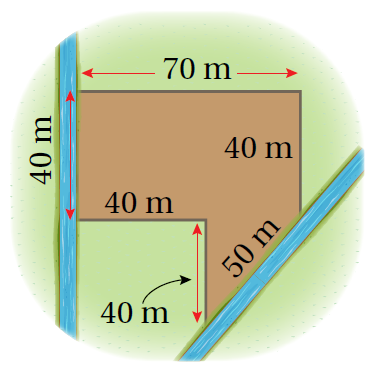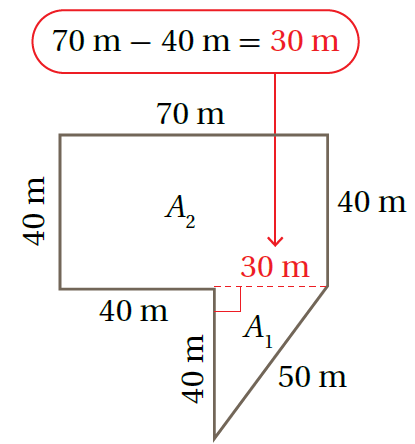${\mathrm{A}}_1=\frac{1}{2}\times b\times h$                     صيغة مساحة المثلث ${\mathrm{A}}_1=\frac{1}{2}\times 30\times 40$ ${\mathrm{A}}_1=600 m^2$ ${\mathrm{A}}_2=w\times l$                      صيغة مساحة المستطيل    ${\mathrm{A}}_2=70\times 40 w=70 m , l=40 m$ ${\mathrm{A}}_2=2800 m^2$ $\mathrm{A}={\mathrm{A}}_1+{\mathrm{A}}_2$   المساحة الكلية تساوي مجموع مساحتي المثلث والمستطيلِ $\mathrm{A}=600+2800$ $\mathrm{A}=3400 m^2$ إِذَنْ، مِساحَةُ قِطْعَةِ الأرْضِ تُساوي $3400 m^2$