فكرةُ الدّرس: أجدُ مساحة شبه المُنحرف، وأحُلُّ مسائل عليها.
|
تعلّمتُ سابقًا أنّ شبه المُنحرف مُضلّعٌ رُباعيٌّ فيه ضلعان مُتوازيان يُسمّيان قاعدتي شبه المُنحرف، ويُرمزُ إليهما بالرّمزين (b1) و (b2) ، وتُسمّى المسافةُ بينهُما ارتفاع شبه المُنحرف (h) كما في الشّكل المُجاور. |
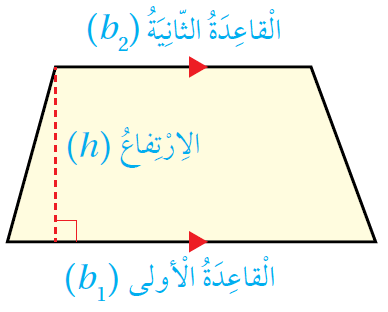 |
|
مفهومٌ أساسيٌّ: مساحةُ شبه المُنحرف بالكلمات: مساحةُ شبه المُنحرف تُساوي نصف مجموع القاعدتين مضروبًا في الارتفاع. بالرُّموز: |
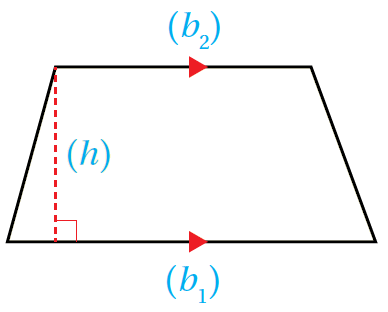 |
مثال
أجدُ مساحة شبه المُنحرف في كُلّ ممّا يأتي:
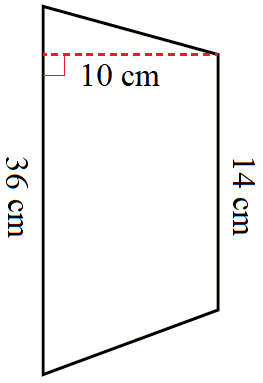 |
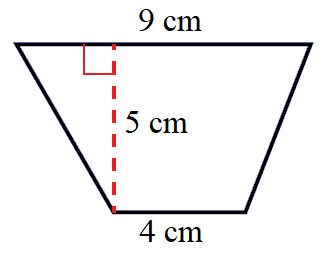 |
| صيغةُ مساحة شبه المُنحرف | صيغةُ مساحة شبه المُنحرف |
يُمكنُ تحديدُ طول قاعدة شبه المُنحرف المرسوم على شبكة مُربّعات وارتفاعه بعدّ المُربّعات، وعندئذ يُمكنُ حسابُ مساحته بالوحدات المُربّعة.
مثال
أجدُ مساحة شبه المُنحرف في الشبكة الآتية:
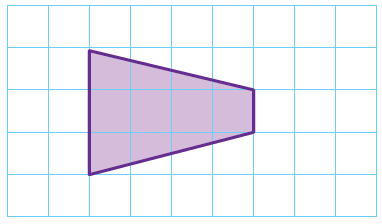 |
الجواب
أبدأُ بعدّ الوحدات الأفُقيّة والرّأسيّة لأجد طول كُلّ من القاعدتين b2 = 1 ، b1 = 3 والارتفاع h = 4
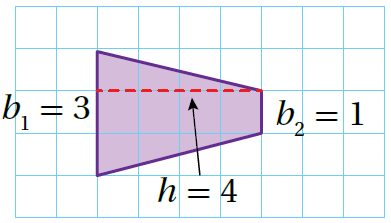 |
يُمكنُ استعمالُ صيغة مساحة شبه المُنحرف في كثير من المواقف الحياتيّة.
|
مثال أجدُ مساحة شبه المُنحرف الظّاهر في الصّورة المُجاورة والنّاتج من مُرور أشعّة الشّمس من خلال نافذة. الجواب إذن؛ مساحةُ شبه المُنحرف النّاتج من مُرور أشعّة الشّمس من خلال النّافذة 1500cm2 |
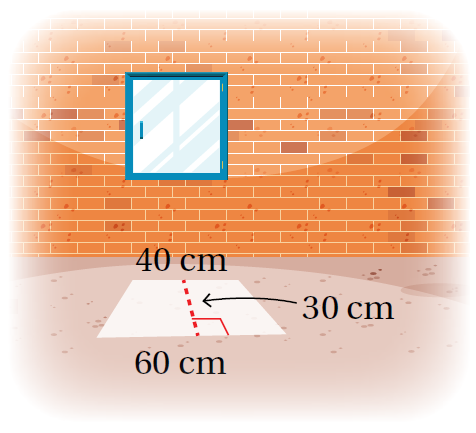 |
يُمكنُ إيجادُ مساحات أشكال مُركّبة تحتوي مُضلّعات من بينها شبهُ المُنحرف.
|
مثال أجدُ مساحة المنطقة المُظلّلة في كُلّ شكل ممّا يأتي: الجواب المنطقةُ المُظلّلةُ هي شبهُ مُنحرف مُفرغٌ منهُ مُثلّثٌ. إذا كانت مساحةُ شبه المُنحرف (A1) ومساحةُ المُثلّث (A2) ، فإنّ مساحة المنطقة المُظلّلة هي: A = A1 - A2 |
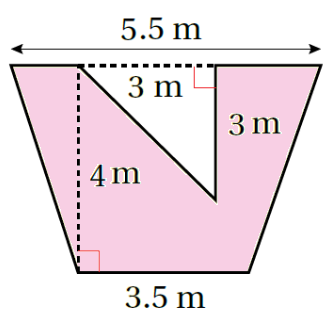 |
| صيغةُ مساحة شبه المُنحرف | |
| صيغةُ مساحة المثلث | |
إذن، مساحةُ شبه المُنحرف تُساوي
إذن، مساحةُ المُثلّث تُساوي
إذن، مساحةُ المنطقة المُظلّلة