رياضيات فصل أول

تطابقُ المثلثاتِ (ASA, AAS)

تعلمنا في الدرس السابق أنه يمكن إثباتُ تطابق  المثلثين باستعمال :

1- ثلاثة أضلاع SSS 

2- ضلعين وزاوية محصورة بينهما SAS

3- ساق ووتر في المثلث قائم الزاوية .

وسنتعلم في هذا الدرس حالتين أخريين :

4- زاويتان وضلع محصور بينهما ASA.

5-زاويتين وضلع غير محصور AAS.

 

ملاحظة : 

يسمّى الضلعُ الواقعُ بَيْنَ زاويتَينِ متتاليتَينِ في مضلعٍ الضلعَ المحصورَ  فمثلاً في المثلث المجاور  $\overline{\mathbf{SQ}}$  هو الضلع المحصور  بين $\mathbf{\angle }\mathit{S}$ و $\mathbf{\angle }\mathit{Q}$ .

 

 

 

 

---

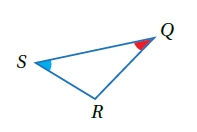
مسلَّمة :  إذا طابقَت زاويتانِ والضلعُ المحصورُ بينَهُما في مثلثٍ نظائرَهُما في مثلثٍ آخَرَ، فإنَّ المثلثَين متطابقانِ وتُختصَرُ هذهِ الحالةُ بالرمزِ ASA .

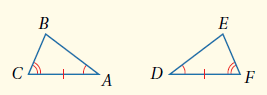
إذا كان : $$\begin{gathered} \overline{\mathbf{A}\mathbf{C}}\mathbf{\cong }\overline{\mathbf{D}\mathbf{F}\mathbf{ }} \\ \mathbf{\angle }\mathit{A}\mathbf{\cong }\mathbf{\angle }\mathit{D} \\ \mathbf{\angle }\mathit{C}\mathbf{\cong }\mathbf{\angle }\mathit{F} \end{gathered}$$ فإن $\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{D}\mathit{E}\mathit{F}$

---

مثال 1 : في الشكل المجاور ، إذا علمت أن $\overline{\mathbf{N}\mathbf{M}}\mathbf{ }\mathbf{\cong }\mathbf{ }\overline{\mathbf{N}\mathbf{P}}$ فأثبت أنَّ $\mathbf{∆}\mathit{N}\mathit{M}\mathit{L}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{N}\mathit{P}\mathit{O}$ باستعمال البرهان ذي العمودين . 

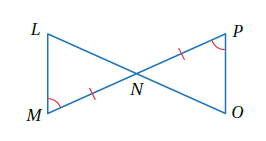
البرهان :

العبارات	المبررات
$\overline{\mathbf{N}\mathbf{M}}\mathbf{\cong }\overline{\mathbf{N}\mathbf{P}}$	معطى
$\mathbf{\angle }\mathit{M}\mathbf{\cong }\mathbf{\angle }\mathit{P}$	معطى
$\mathbf{\angle }\mathit{M}\mathit{N}\mathit{L}\mathbf{\cong }\mathbf{\angle }\mathit{P}\mathit{N}\mathit{O}$	زاويتان متقابلتان بالرأس
$\mathbf{∆}\mathit{N}\mathit{M}\mathit{L}\mathbf{ }\mathbf{\cong }\mathbf{∆}\mathit{N}\mathit{P}\mathit{O}$	ASA

 

---

نظرية :  إذا طابقَت زاويتانِ وضلع غيرُ محصورٍ بينَهُما في مثلثٍ نظائرَهُما في مثلثٍ آخَرَ، فإنَّ المثلثَين متطابقانِ. وتُختصَرُ هذهِ الحالةُ بالرمزِ AAS.

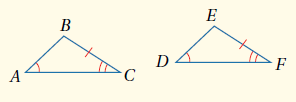
إذا كان : $$\begin{gathered} \overline{\mathbf{BC}}\mathbf{\cong }\overline{\mathbf{EF}\mathbf{ }} \\ \mathbf{\angle }\mathit{A}\mathbf{\cong }\mathbf{\angle }\mathit{D} \\ \mathbf{\angle }\mathit{C}\mathbf{\cong }\mathbf{\angle }\mathit{F} \end{gathered}$$  فإن $\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{D}\mathit{E}\mathit{F}$.

---

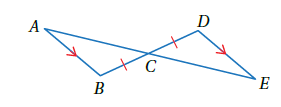
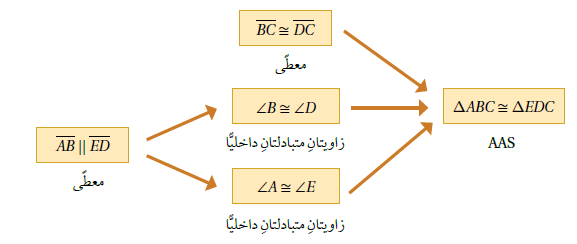
مثال 2 : في الشكل المجاور ، إذا علمت أن $\overline{\mathbf{B}\mathbf{C}}\mathbf{ }\mathbf{\cong }\mathbf{ }\overline{\mathbf{D}\mathbf{C}}$  و $\overline{\mathbf{A}\mathbf{B}}\mathbf{\parallel }\mathbf{ }\overline{\mathbf{E}\mathbf{D}}$ ، فأثبت أن $\mathbf{∆}\mathit{A}\mathit{B}\mathit{C}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{∆}\mathit{E}\mathit{D}\mathit{C}$ باستعمالِ البرهانِ السهميِّ.

---

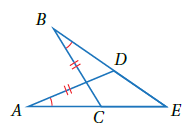
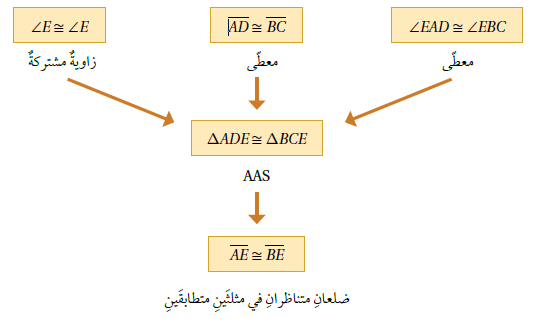
مثال 3  :  في الشكلِ المجاورِ، إذا علمْتُ أنَّ $\mathbf{\angle }\mathit{E}\mathit{A}\mathit{D}\mathbf{ }\mathbf{\cong }\mathbf{\angle }\mathbf{ }\mathit{E}\mathit{B}\mathit{C}\mathbf{ }\mathbf{,}\mathbf{ }\overline{\mathbf{A}\mathbf{D}}\mathbf{\cong }\overline{\mathbf{B}\mathbf{C}}$ . فأثبتُ أنَّ $\overline{\mathbf{A}\mathbf{E}}\mathbf{ }\mathbf{\cong }\overline{\mathbf{ }\mathbf{B}\mathbf{E}}$ باستعمالِ البرهانِ السهميِّ.

---

مثال 4: منَ الحياةِ .

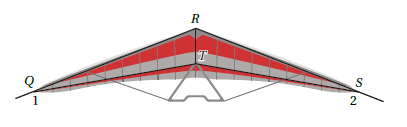
طائرةٌ شراعيةٌ : يصمَّمُ جناحا الطائرةِ الشراعيةِ بحيثُ يبدُوانِ مثلثَينِ متطابقَينِ كما في الشكلِ المجاورِ؛ لضمانِ توازنِ الطائرةِ في الجوِّ. إذا كانت $\mathbf{\angle }\mathbf{1}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{\angle }\mathbf{2}$ فأثبت أن $\overline{\mathbf{Q}\mathbf{T}}\mathbf{ }\mathbf{\cong }\mathbf{ }\overline{\mathbf{S}\mathbf{T}}$ .

العبارات	المبررات
$\mathbf{\angle }\mathbf{1}\mathbf{ }\mathbf{\cong }\mathbf{ }\mathbf{\angle }\mathbf{2}$	معطى
$\mathbf{\angle }\mathit{R}\mathit{T}\mathit{Q}\mathbf{\cong }\mathbf{\angle }\mathit{R}\mathit{T}\mathit{S}$	معطى
$\mathbf{\angle }\mathit{R}\mathit{Q}\mathit{T}\mathbf{\cong }\mathbf{\angle }\mathit{R}\mathit{S}\mathit{T}$	زاويتانِ متكاملتانِ مَعَ الزاويتَينِ المتطابقتَينِ $\mathbf{\angle }\mathbf{1}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{\angle }\mathbf{2}$
$\overline{\mathbf{R}\mathbf{T}}\mathbf{ }\mathbf{\cong }\mathbf{ }\overline{\mathbf{R}\mathbf{T}}$	ضلعٌ مشتركٌ
$\mathbf{∆}\mathit{R}\mathit{Q}\mathit{T}\mathbf{ }\mathbf{\cong }\mathbf{∆}\mathit{R}\mathit{S}\mathit{T}$	AAS
$\overline{\mathbf{Q}\mathbf{T}}\mathbf{ }\mathbf{\cong }\mathbf{ }\overline{\mathbf{S}\mathbf{T}}$	ضلعانِ متناظرانِ في مثلثَينِ متطابقَينِ

 

---