رياضيات7 فصل أول

مفهوم أساسي : 

الاقتران (Function) : هوَ علاقةٌ تربطُ كلَّ قيمةٍ منَ المُدخلاتِ بقيمةٍ واحدةٍ فقطْ منَ المُخرجاتِ. ويمكنُني التعبيرُ عنِ الاقترانِ بطرائقَ مختلفةٍ كما يأتي:

اقتران علاقته : أجمعُ 3 ثمَّ أقسمُ على 2

على صورةِ آلةِ اقترانٍ:

المخرجة			المدخلة
y	$\stackrel{\mathbf{÷}\mathbf{2}}{\mathbf{\to }}$	$\stackrel{\mathbf{+}\mathbf{3}}{\mathbf{\to }}$	x

بالصّورةِ الجبريّةِ:

$$\begin{gathered} \mathbf{x}\underset{}{\mathbf{\to }}\frac{\mathbf{x}\mathbf{+}\mathbf{3}}{\mathbf{2}} \\ \mathbf{y}\mathbf{=}\frac{\mathbf{x}\mathbf{+}\mathbf{3}}{\mathbf{2}} \end{gathered}$$

على صورةِ جدولِ مدخلاتٍ ومخرجاتٍ:

المخرجة y	المدخلة x
$\frac{\mathbf{1}+3}{2}=2$	1
$\frac{\mathbf{2}+3}{2}=2.5$	2
$\frac{\mathbf{3}+3}{2}=3$	3

على صورةِ مخطّطٍ سهميٍّ:

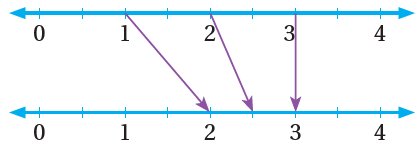
مثال 1 : أكملُ جدولَ المدخلاتِ والمخرجاتِ لكلِّ اقترانٍ ممّا يأتي:

1) $\mathbf{y}\mathbf{=}\mathbf{2}\mathbf{x}\mathbf{-}\mathbf{5}$

المخرجة y	المدخلة x
2(1)-5 = -3	1
2(2)-5 = -1	2
2(3)-5 = 1	3
2(4)-5 = 3	4

2) $\mathbf{y}\mathbf{=}\mathbf{3}\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{1}\mathbf{)}$

المخرجة y	المدخلة x
3(1+1) = 6	1
3(2+1) = 9	2
3(3+1) = 12	3
3(4+1) = 15	4

 

يمكنُني أنْ أستخدمَ آلةَ الاقترانِ لأكتبَ قاعدتَهُ بالصورةِ الجبريّةِ 

مثال2 : أكتبُ قاعدةَ كلِّ اقترانٍ ممّا يأتي جبرِيًّا:

1) $\mathbf{x}\stackrel{}{\mathbf{\to }}\boxed{\mathbf{\times }\mathbf{6}}\mathbf{ }\stackrel{}{\mathbf{\to }}\boxed{\mathbf{-}\mathbf{2}}\stackrel{}{\mathbf{\to }}$

آلةُ الاقترانِ المعطاةُ تضربُ المدخلةَ x في 6، ثمَّ تطرحُ 2 

إذنْ، يمكنُني كتابةُ قاعدةِ الاقترانِ بالصّورةِ الجبريّةِ على الشكلِ: $\mathrm{x}\stackrel{}{\to }6\mathrm{x}-2$ أوْ كمعادلةٍ على الشكلِ: $\mathrm{y}=6\mathrm{x}-2$

2) $\mathbf{x}\stackrel{}{\mathbf{\to }}\boxed{\mathbf{+}\mathbf{9}}\mathbf{ }\stackrel{}{\mathbf{\to }}\boxed{\mathbf{\times }\mathbf{5}}\stackrel{}{\mathbf{\to }}$

 آلةُ الاقترانِ المعطاةُ تجمعُ 9 معَ المدخلةِ x ، ثمَّ تضربُ ناتج الجمع في 5 

إذنْ، يمكنُني كتابةُ قاعدةِ الاقترانِ بالصّورةِ الجبريّةِ على الشكلِ: $\mathrm{x}\stackrel{}{\to }\left(\mathrm{x}+9\right)\times 5$ ، أوْ كمعادلةٍ على الشكلِ: $\mathrm{y}=\left(\mathrm{x}+9\right)\times 5$

 

يمكنُ استعمالُ جدولِ المدخلاتِ والمخرجاتِ لكتابةِ قاعدةِ الاقترانِ بالصورةِ الجبريّةِ.

مثال 3 : يبيِّنُ الجدولُ المجاورُ قِيَمَ المدخلاتِ والمخرجاتِ لاقترانٍ:

المخرجة y	المدخلة x
-1	1
2	2
5	3
8	4

1) أصِفُ بالكلماتِ قاعدةَ الاقترانِ.

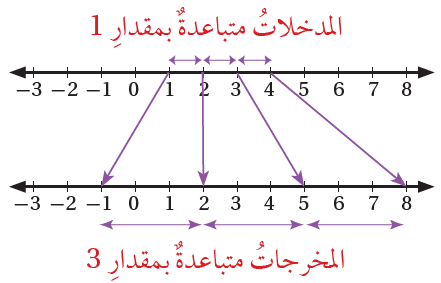
بما أنَّ المدخلاتِ متباعدةٌ بمقدارِ 1، والمخرجاتِ متباعدةٌ بمقدارِ 3، فإنَّ الجزءَ الأوّلَ منَ القاعدةِ هوَ: الضربُ في 3 ، وحتى تكونَ صورةُ العددِ 4 هيَ 8، يجبُ أنْ تحتويَ القاعدةُ على طرْحِ العددِ 4.

إذنْ، قاعدة الاقترانِ هيَ: أضربُ في 3 ثمَّ أطرحُ 4 

2) أكتبُ قاعدةَ الاقترانِ بالصورةِ الجبريّةِ. 

يمكنُني كتابةُ قاعدةِ الاقترانِ بالصورةِ الجبريةِ كما يلي:

$\mathrm{x}\stackrel{}{\to }3\mathrm{x}-4$

أوْ كمُعادلةٍ بالصورةِ الآتيةِ:

$\mathrm{y}=3\mathrm{x}-4$