المهارات الرقمية12 فصل أول

الدالة الراجعة

     سبق وان قمنا بكتابة برنامج يقوم بحساب مضروب العدد في الدرس السابق من خلال لغة البرمجة بايثون،حيث تم استخدام أسلوب الحلقات في هذه العملية.ولأنّ البرنامج الجيد هو البرنامج الذي يؤدي مهامه ويقوم بحل المسألة بأقصر وأفضل الطرق، كان لا بدّ من التعرف على الدوال  او ما يسمى بـ (Functions)  التي يمكن مناداتها في اللحظة التي نحتاجها وفي أي موقع من داخل البرنامج.

 

إنّ استخدام هذه الدوال له أهمية كبيرة في عالم البرمجة حيث:

•  تنظيم الكود،إذ يتم تقسيم المشاكل المعقدة إلى أجزاء أصغر مما يسهل قراءة الكود وفهمه ويساعد على صيانة الكود في المستقبل.

 

• توفير الوقت والجهد ، حيث يمكن استدعاء الدالة في أجزاء مختلفة من البرنامج وبالوقت الذي نحتاجه دون الحاجة الى إعادة كتابة نفي الاوامر وتكرارها ، وعليه أصبح بديلًا لعمليات الدوران والتكرار.

 

• المرونة في تطبيق الدالة على قيم مختلفة من خلال تمرير المعاملات المختلفة مما يساعد على أداء نفس المهمة بعدة طرق.

 

 

 

 

 

 

 

 

 

 

ولنعد الى مثال إيجاد المضروب لعدد معين على سبيل المثال :

حسب ما تعلمنا في الرياضيات،فإن مضروب العدد 6 هو:

6!= 6*5*4*3*2*1

ومضروب العدد 5 هو :

5!=5*4*3*2*1

ومضروب العدد 4 هو :

4!=4*3*2*1

وهكذا الى أن نصل الى مضروب العدد 1 والذي يساوي 1

أي أننا يمكننا القول بأن مضروب العدد 6 هو حاصل ضرب العدد 6 في مضروب العدد 5

ومضروب العدد 5 هو حاصل ضرب العدد 5 في مضروب العدد 4

وكأننا كل مرة نستدعي دالة المضروب للعدد الذي يسبق العدد الذي نريد ايجاد المضروب له.

 

 

الصيغة العامة للدالََّة الراجعة (Recursive Function) في لغة البرمجة بايثون

أن الصيغة العامة لكتابة الدالة الراجعة

 تظهر في الشكل التالي وتتألف مما يلي: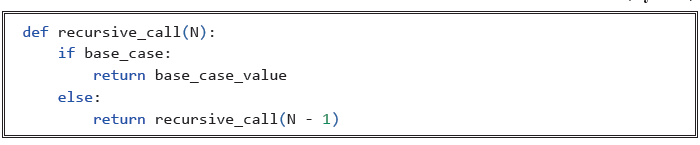

 

def: كلمة محجوزة وتستخدم لتعريف أي دالة جديدة.

recursive_call: اسم الدالة والتي يكون لها مدخلات معينة يتم وضعها داخل أقواس وهنا تم وضع حرق (N) حيث يمثل عدد صحيح

base_case:القيمة الأساسية التي تجعل الدالة تتوقف عن العمل، وعدم وجودها يعني ان البرنامج يوف يدخل في حالة دوران لا نهائي.

base_case_value: قيمة القيمة الأساسية والتي تعود الى الرنامج عند تحقق شرط الوصول الى القيمة الأساسية.

 

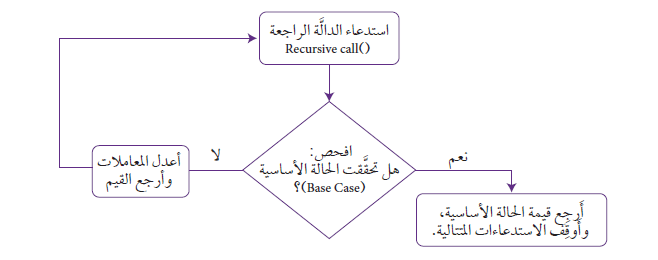
ويمكن تمثيل مخطط سير العمليات للدالة الراجعة كما يظهر بالشكل التالي:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

استخدام المكدس في تتبُُّع حالة كل استدعاء للدالََّة الراجعة:

سبق لنا وان تعرفنا على المكدس (stack) وقمنا بذكره على أنه نوع من أنواع هياكل البيانات. ولنوضح العلاقة التي يتم استخدام المكدس (stack) فيها مع الدالة الراجعة دعنا نتخيل ما يلي:

تخيل المكدس (stack) على أنه شيء يشبه الوعاء مفتوح من الاعلى ومغلق من الاسفل ويتم وضع فيه الاشياء فوق بعضه(أي تكديس الأشياء).

وبما أنّ الأشياء توضع فوق بعضها البعض، فإن ما يدخل بالأخير سوف يخرج أولاً (Last In First Out ) والتي يرمز لها (LIFO ). ولتوضيح هذه القاعدة لنأخذ المثال التالي:

 

 

مثال:

أحضر صندوقا مفتوح من الأعلى فقط

أحضر ثلاثة كتب وقم بترقيمهاالكتاب رقم 1، الكتاب رقم 2،

والكتاب رقم 3

قم بوضغ الكتب في الصندوق على الترتيب التالي:

الكتاب رقم1

الكتاب رقم 2

الكتاب رقم 3

والآن، إن حاولنا إخراج الكتب، فإن الكتاب رقم 1 أصبح في قاع الصندوف والكتاب رقم 3 أصبح في القمة.

واذا تم الطلب بإخراج الكتاب الذي في أعلى الصندوق، سوف يتم إخراج الكتاب رقم 3 وهذا هو مبدأ (LIFO) ما يدخل آخيرًا يخرج أولًا.

 

والآن دعنا نستخدم المكدس (Stack) في تتبع حالة إستدعاء للدالة الراجعة  حسب مثالنا السابق والذي يعمل على إيجاد مضروب العدد(6).

كما سبق وتعلمنا، فإن مضروب العدد 6 هو:

6! = 6*5*4*3*2*1  = 720

 

وكما شرحنا سابقاً، فإنّ مضروب العدد 6 ممكن التعبير عنه من خلال:

6!= 6*5!

 

أي أننا يمكن أن نستنتج بأن الصيغة العامة لإيجاد مضروب أي عدد هي:

مضروب (العدد) = العدد * مضروب (العدد -1)

وبالصيغية الرياضية، دعنا نرمز للعدد بالرمز (n) وللدالة الخاصة بالمضروب بالرمز (fact):

 

fact(n) = n* fact (n-1)

 

ومن خلال لغة بايثون ، فإن البرنامج الذي سوف يحقق الامر هو:

def fact (n):

if n == 0 or n == 1:             #  الحالة الأساسية التي توقف التكرار  

else:

return n * fact (n - 1)        # استدعاء الدالة بشكل مكرر

والأن لنرى كيف يتم إدخال المعلومات داخل المكدس حسب المثال:

1. الاستدعاءات التكرارية (بناء الكدسة):

       factorial(6) → ينتظر نتيجة factorial(5)

 يتم وضعها في أسفل المكدس   ويتم وضع مؤشر يشير اإلى آخر شيء دخل على المكدس (Top)

factorial(5) → ينتظر نتيجة factorial(4)

 يتم وضعها فوق ( factorial(6) ) في المكدس  ويتم وضع مؤشر يشير اإلى آخر شيء دخل على المكدس (Top) وهكذا بالنسبة لبقية الأوامر  التالية:

factorial(4) → ينتظر نتيجة factorial(3)

factorial(3) → ينتظر نتيجة factorial(2)

factorial(2) → ينتظر نتيجة factorial(1)

factorial(1) → يصل إلى الحالة الأساسية ويعيد 1

وعليه تصبح (factorial(1)) في أعلى المكدس و (factorial(6)) في أسفل المكدس

وعند القيام بعملية تفريغ المكدس (حساب النتائج):

فإنّ أخر قيمة دخلت الى المكدس  هي التي سوف يتم إخراجها منه وحساب قيمتها  أي

factorial(1) يعيد    1

factorial(2)   يعيد  2 * 1 = 2

factorial(3) يعيد    3 * 2 = 6

factorial(4) يعيد    4 * 6 = 24

factorial(5) يعيد    5 * 24 = 120

factorial(6) يعيد    6 * 120 = 720

وهذا تماما حسب ما تعلمناه عن مبدأ المكدس (Stack) والذي يقوم على من يدخل أخيرا يخرج أولًا (LIFO)

 

ملاحظة هامة :

إنّ إستدعاء الدالة لنفسها عدد كبير من المرات، يزيد من حجم الذاكرة المستخدمة وذلك لأن كل مرة الدالة تنادي نفسها يتم وضع إطار يشير إلى الأعلى. وفي حال عدم وجود الحالة الأساسية التي تعمل على توقف عملية الإستدعاء (Base case) فإنّ الدالة سوف سيتم استدعاءها بشكل لانهائي وهذا سيسبب إمتلاء حجم الذاكرة او ما يطلق عليه (stack overflow ) بالتالي يعطل الجهاز نفسه وسيضطر البرنامج الى اغلاق نفسه.