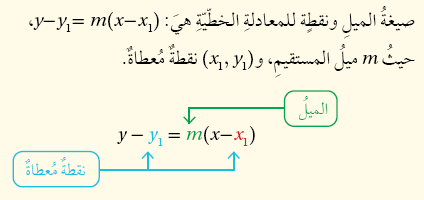
أتحقق من فهمي (1)
1) أكتبُ معادلةَ المستقيمِ المارِّ بالنقطةِ وميله بصيغة الميل والنقطة
2) أكتبُ معادلةَ المستقيمِ المارِّ بالنقطتينِ بصيغةِ الميلِ ونقطةٍ.
1) الميل
2) معادلة المستقيم نعوض النقطة
أتحقق من فهمي (2)
1)
2)
3)
أتحقق من فهمي (3)
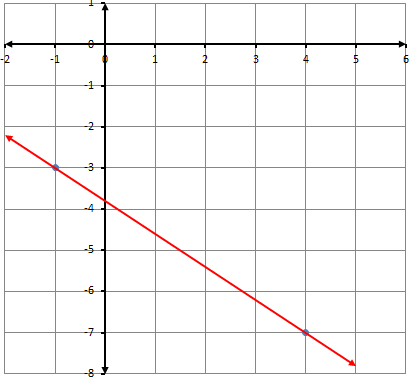
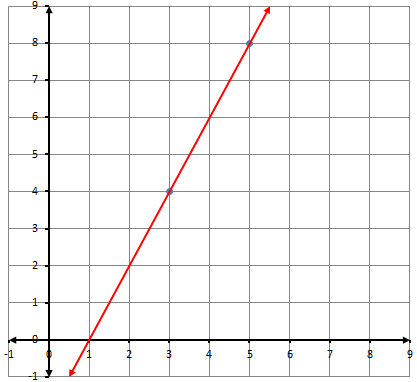
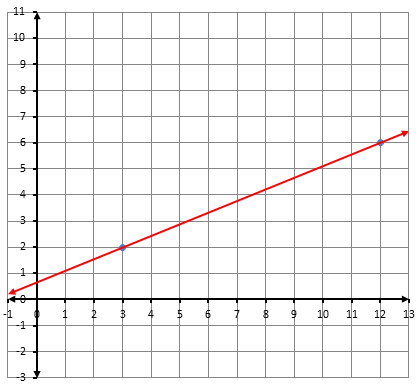
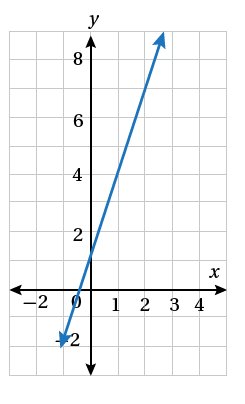
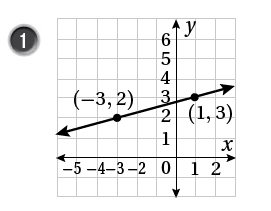
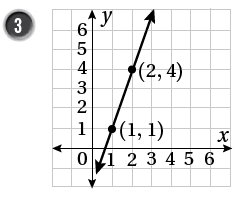
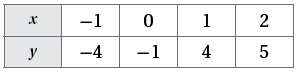
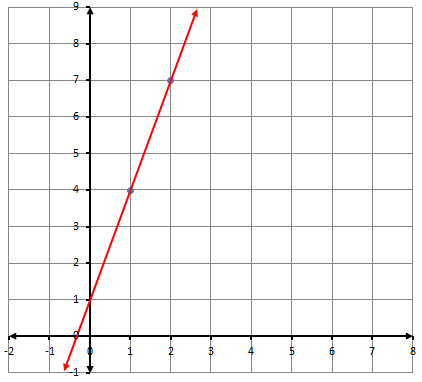
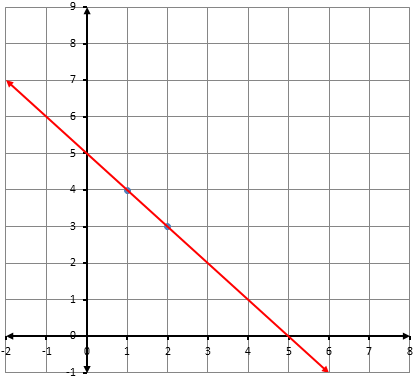
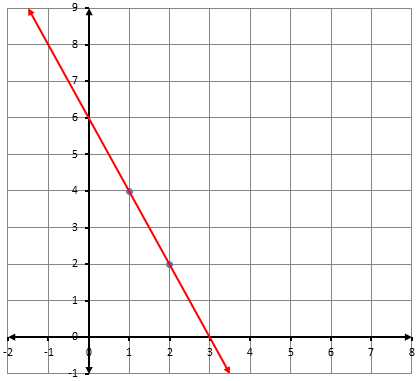
أكتبُ معادلةَ المستقيمِ المُمَثَّلِ بيانيًّا في كلٍّ ممّا يأتي بصيغةِ الميلِ ونقطةٍ:
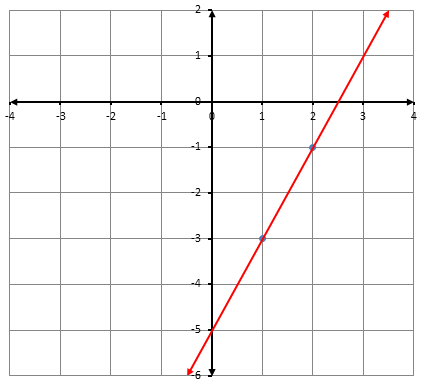
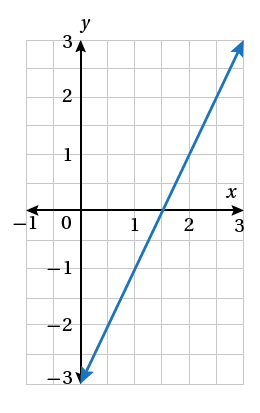
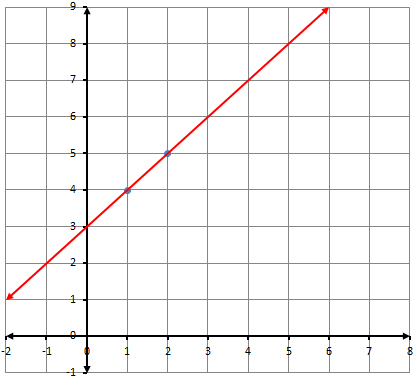
1)
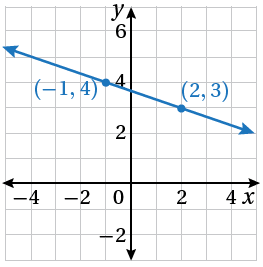
معادلة المستقيم نعوض النقطة
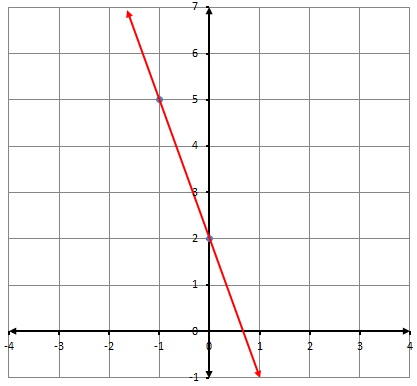
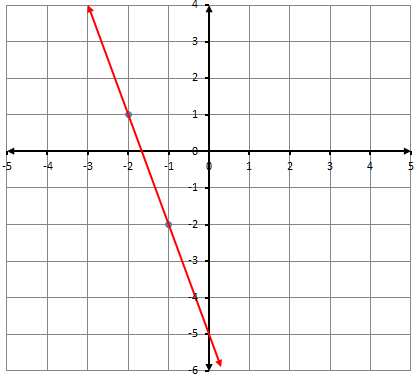
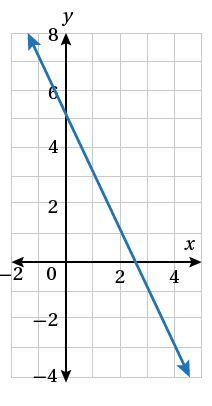
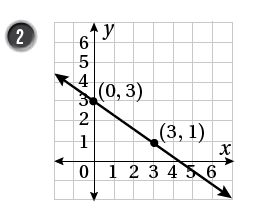
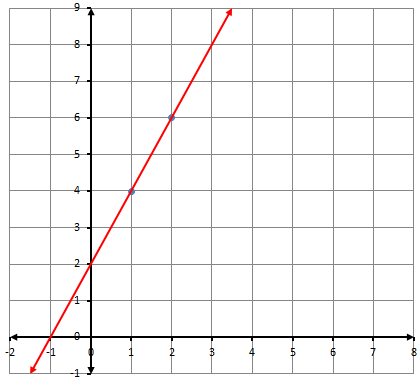
2)
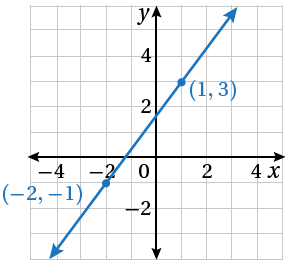
معادلة المستقيم نعوض النقطة
أتحقق من فهمي (4)
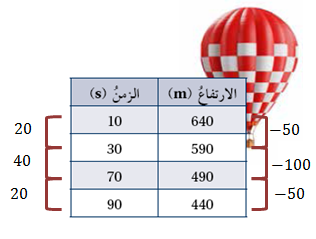
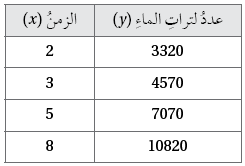
منطادٌ: يبيّنُ الجدولُ المجاورُ العلاقةَ بينَ ارتفاعِ منطادِ هواءٍ ساخنٍ والزمنِ.
1) 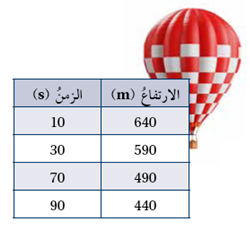
إذنْ، العلاقةُ بينَ ارتفاع المنطاد والزمن خطيّةٌ (عكسية)، ومعدّلُ التغيُّرِ هو لكلِّ ثانية.
2) أكتبُ معادلةً خطّيةً بمتغيرينِ بصيغةِ الميلِ ونقطةٍ يمكنُ استعمالُها لإيجادِ ارتفاعِ المنطادِ عندَ أيِّ لحظةٍ.
أتدرب وأحل المسائل
أكتبُ معادلةَ المستقيمِ المارِّ بالنقطةِ المُعْطاةِ والمعلومِ ميلُه m في كلٍّ ممّا يأتي بصيغةِ الميلِ ونقطةٍ:
أكتبُ معادلةَ المستقيمِ المارِّ بكلِّ نقطتينِ ممّا يأتي بصيغةِ الميلِ ونقطةٍ:
أمثّلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا باستعمالِ الميلِ ونقطةٍ:
أكتبُ بصيغةِ الميلِ ونقطةٍ معادلةَ المستقيمِ الممثَّلِ بيانيَّا في كلٍّ ممّا يأتي:
9)
10)
11)
12) جَبْرٌ: إذا كانَ ميلُ المستقيمِ المارِّ بالنقطتينِ يساوي 5 فأجدُ قيمةَ الثابتِ
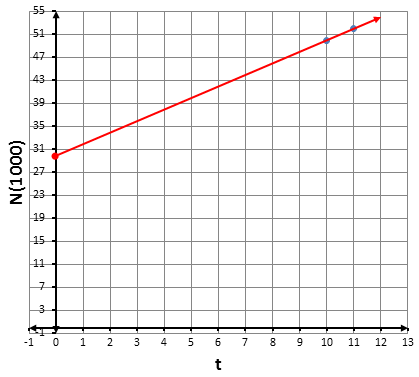
بَعوضٌ: تمثّلُ المعادلةُ عددَ البعوضِ N بالآلافِ في مستنقعٍ صغيرٍ بعدَ t يومًا من بدايةِ شهرِ حزيرانَ.
13) أمثّلُ المعادلةَ بيانيًّا، حيثُ t ≥ 0
14) بعدَ كمْ يومٍ منْ بدايةِ الشهرِ يكونُ عددُ البعوضِ في المستنقعِ 46000 ؟
بعد 12 يوماً
بيئةٌ: التمثيلُ البيانيُّ المجاورُ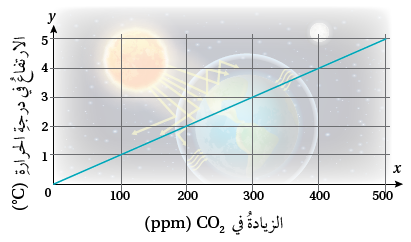
15) إذا زادَ بمقدارِ ، فما الارتفاعُ المتوقَّعُ في درجةِ الحرارةِ؟
يتوقع ازدياد درجة الحرارة بمقدار 3.6 درجة حسب التمثيل البياني
16) ارتفعتْ درجةُ الحرارةِ بينَ عامَيْ 1980 م و 2000 بمقدارِ 0.4 °C أجدُ مقدارَ الزيادةِ في كميّةِ ثاني أكسيدِ الكربونِ.
مقدار الزيادة في كمية ثاني أكسيد الكربون تساوي
17) أكتبُ معادلةً خطّيةً بمتغيرينِ يمكنُ استعمالُها لإيجادِ مقدارِ الارتفاعِ في درجةِ الحرارة عند أي ارتفاع في كمية في الغلاف الجوي
أشجارٌ: يبيّنُ الجدولُ المجاورُ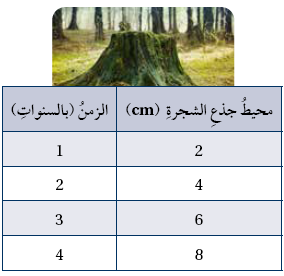
18) أبيّنُ أنَّ العلاقةَ بينَ محيطِ جِذْعِ الشجرةِ والزمنِ خطّيةٌ.
العلاقة بين محيط جذع الشجرة والزمن هي علاقة خطية ومعدل التغير هو لكل سنة
19) أتنبّأُ بمحيطِ جذعِ الشجرةِ بعدَ 10 سنواتٍ.
20) أكتبُ معادلةً خطّيةً بمتغيرينِ يمكنُ استعمالُها لإيجاِد محيطِ جذعِ الشجرةِ في أيِّ سنةٍ.
21) تبريرٌ: أوجَدَ كلٌّ منْ باسمٍ ولينَ معادلةَ المستقيمِ المارِّ بالنقطتينِ ( 6 , 1) ,(6-, 2-) على النحوِ الآتي:
هلْ إجابةُ كلٍّ منهُما صحيحةٌ؟ أبرّرُ إجابتِي.
إجابة كل منهما صحيحة ولكن كلاً منهما استخدم نقطة مختلفة عن الأخر
22) تبريرٌ: كيفَ سيتغيّرُ التمثيلُ البيانيُّ للمعادلةِ (y - 12 = 8(x -2 ، إذا تغيّرتْ إشاراتا الطرحِ في المعادلةِ إلى إشاراتي جمعٍ؟ أبرّرُ إجابتي دونَ اللجوءِ إلى تمثيلِ المعادلةِ بيانيًّا.
سيكون لدينا مستقيم أسفل المستقيم الأصلي وموازي له
23) تبريرٌ: أجدُ معادلةَ المستقيمِ المارِّ بالنقطتينِ ( 5 , 5) ,( 1 , 9) بصيغةِ الميلِ والمقطعِ، ثمَّ أُبيّنُ أنَّ المقطعَ x يساوي 10 مبرِّرًا إجابتِي.
نعوض لإيجاد المقطع x
24) أكتبُ: كيفَ أكتبُ معادلةَ مستقيمٍ إذا عُلمَ ميلُهُ ونقطةٌ يمرُّ بِها؟
كتاب التمارين
أكتبُ معادلةَ المستقيمِ الممثلةَ بيانيًّا في كلٍّ ممّا يأتي بصيغةِ الميلِ ونقطةٍ:
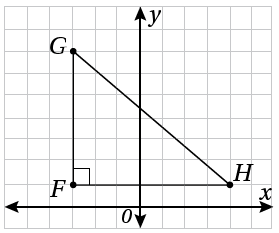
يبيّنُ التمثيلُ البيانيُّ المجاورُ المثلثَ القائمَ الزاويةِ : GHF
4) أكتبُ معادلةً بصورةِ الميلِ ونقطةٍ تمثلُ المستقيمَ الّذي يحوي
5) أكتبُ معادلةً بصورةِ الميلِ ونقطةٍ تمثلُ المستقيمَ الّذي يحوي
يبيّنُ الجدولُ المجاورُ عددَ لتراتِ الماءِ y في خزّانٍ بعدَ x ساعةً:
6) أبيّنُ ما إذا كانَتِ العلاقةُ بَيْنَ عددِ لتراتِ الماءِ في الخزّانِ والزمنِ خطيةً أَم لا.
العلاقة بين عدد لترات الماء والزمن خطية ومعدل التغير يساوي لتر لكل ساعة
7) أكتبُ معادلةً خطيةً بمتغيرَينِ تمثلُ البياناتِ بصيغةِ الميلِ ونقطةٍ.
8) أكتشفُ الخطأَ: تقولُ مرامُ إنَّ جدولَ القِيَمِ الآتِيَ يمثلُ علاقةً خطيةً بَيْنَ x وَ y
معدل التغير ليس ثابت وعليه العلاقة ليست خطية
9) مسألةٌ مفتوحةٌ: أكتبُ 5 معادلاتٍ خطيةٍ بمتغيرَينِ تمرُّ بالنقطةِ ( 4 , 1)، ثُمّ أمثلُ كلَّ معادلةٍ مِنْها في المستوى الإحداثيِّ.