امتحان تجريبي فصل اول رياضيات- مصطفى العفوري

1- إذا كان $f\left(x\right)=x^3+a^2{x}^2+3 ,a>0$ , وكانت $\underset{h\to 0}{lim} \frac{f(-2+h)-f(-2)}{2h}=-2$   , فإن قيمة الثابت  a تساوي :

2- إذا كان $f\left(x\right)=\ln \left(\frac{x}{e^2}\right)$ , فإن $\frac{f\left(1\right)}{f^{\backslash }\left(1\right)}$ تساوي

3- إذا كان $y={(x+1)}^{x+1}$ , فإن $\frac{dy}{dx}$ عندما $x=1$ تساوي 

4- إذا كان $f\left(x\right)=e^{2x}+\frac{1}{e^{2x}}$ , فإن $f^{\backslash \backslash }\left(x\right)$ تساوي 

5- إذا كان $h\left(x\right)= \frac{\sqrt{4+3f^2\left(x\right)}}{\sqrt{28}}$ , وكان $f\left(1\right)=\sqrt{7}$ , $f^{\backslash }\left(1\right)=2$ , فإن $h^{\backslash }\left(1\right)$ تساوي :

6- واحد من الاقترانات التالية له مماس أفقي : 

7- ميل العمودي على المماس لمنحنى العلاقة ${(x+y)}^3=x^2+y$ عند $x\ne 0 , y=0$ هو

8- إذا كان $y=\sin 2t , x=\cos 2t$ , فإن $\frac{d^{2}y}{d{x}^2}$ عندما $t=\frac{\mathrm{\pi }}{6}$ تساوي

9- إذا كان $f\left(x\right)=3^x\ln \left(ex\right)-3x$ , فإن معادلة المماس للاقتران عند  $x=1$ هي :

10- يتحرك جسم بحيث يتحدد موقعه بالعلاقة $s\left(t\right)=a \sin 3t +b \cos 3t$ , فإن تسارع الجسم عندما $s=4m$ ٌساوي 

11- إذا كان $f\left(x\right)=x+se{c}^{2}x , g\left(x\right)=\mathrm{\pi x}$ , فإن قيمة ${(f\circ g)}^{\backslash }\left(\frac{1}{4}\right)$ هي : 

12- النقطة الواقعة على منحنى العلاقة ${(y-4)}^2=x+2$ , والتي يكون عندها المماس موازياً للمستقيم $3x+6y+2=0$ 

13- قيمة x التي يكون للاقتران $f\left(x\right)=(x-2){(x-3)}^2$ عندها قيمة عظمى محلية هي : 

14- إذا كان $f\left(x\right)={\cos }^{3}x$ حيث  $x\in [0,\mathrm{\pi }]$ , فإن $f\left(x\right)$ يكون متناقص في :

15- وجد مصنع للاثاث أن التكلفة الكلية لإنتاج غرف نوم عددها x تعطى بالعلاقة $f\left(x\right)=x^3+3x^2-80x+500$ , إذا تم بيع كل غرفة نوم بمبلغ $2800JD$ فإن الانتاج اللازم لتحقيق أكبر ربح ممكن هو

16- مثلث متطابق الاضلاع يتمدد بفعل الحرارة يزداد طول ضلعه بمعدل $\left(m\right)cm/min$ فإن معدل تغير مساحته عندما يكون طول ضلعه $\frac{1}{m}$ يساوي

17- إذا كان $z=-2+\sqrt{-12}$ , فإن $Arg(\stackrel{-}{z)}$ تساوي :

18- إذا كان $z=\frac{3-5i}{4+3i}$ , فإن مقياس العدد المركب z يساوي

19- إذا كان $z=-2-2i$ , فإن الصورة المثلثية للعدد المركب z هي

20- ناتج $12\left(\cos \right(\frac{\mathrm{\pi }}{3})+i\sin (\frac{\mathrm{\pi }}{3}\left)\right)÷2\left(\cos \right(\frac{\mathrm{\pi }}{6})+i\sin (\frac{\mathrm{\pi }}{6}\left)\right)$ يساوي  : 

21- إذا كان a,b>0 , وكان $w=a-bi$ حيث $Arg\left(w\right)=\frac{-\mathrm{\pi }}{5}$ وكان $z=-3b-3ai$ فإن $Arg\left(z\right)$ تساوي :

22- واحدة من المعادلات التالية تمثل الصيغة الديكارتية للمعادلة $|z-2+3i|=5$ 

بالاعتماد على الشكل المجاور الذي يمثل منحنى لأولى للاقتران $f\left(x\right)$ المعرف على $[-4,4]$ أجب عن الفقرتين $(23,24)$ 

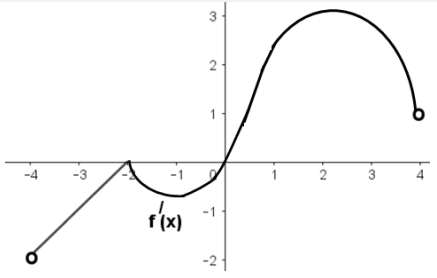
23- مجموعة قيم x الحرجة للاقتران $f\left(x\right)$ هي : 

24- يكون الاقتران $f\left(x\right)$ مقعر للاسفل في