أخطاء القياس

أخطاء القياسِِس
الدرس  Measurment  Errors 

لا تخلو أيُّ عمليّةِ قياسٍ منَ الأخطاءِ، إذْ يوجدُ دائمًا عدمُ يقينٍ Uncertainty

 إلى درجةٍ ما في القياساتِ التي نحصلُ عليها، إذْ لا نستطيعُ أنْ نُؤكّدَ بأنَّ

 قياساتِنا دقيقةٌ تمامًا مهما بلغتْ دقّةُ الأدواتِ المُستخدَمةِ في عمليّةِ

 القياسِ. وهذا يعودُ إلى أسبابٍ عدّةٍ يمكنُ إجمالُها بما يُسمَّى الأخطاءَ التجريبيّةَ .

 الأخطاءُ التجريبيّةُ Experimental Errors يشيرُ الخطأُ التجريبيُّ إلى الفرقِ بينَ

 القيمةِ المقاسة  والقيمة الحقيقيةِ (الصحيحةِ) للكميّةِ الفيزيائيةِ. والأخطاءُ

 التجريبيةُ بوجهٍ عامٍّ تُقسمُ إلى عشوائيةٍ ومنتظمةٍ.

الأخطاءُ العشوائيّةُ Random Errors

 وهي الأخطاءُ التي لا تأخذُ نمطًا محدّدًا عندَ تكرارِ عمليةِ القياسِ تحتَ

 الظروفِ نفسِها،   إذْ تكونُ بعضُ القيمِ (القياساتِ) أكبرَ منَ القيمةِ

 الحقيقيّةِ، وبعضُها الآخرُ أقلَّ، ولا يتكرّرُ مقدارُ الخطأِ نفسُه بتكرارِ

 التجربةِ (المحاولةِ)  ومنْ مصادرِ الأخطاءِ العشوائيّةِ، التذبذباتُ التقلّباتُ

 Fluctuations في قراءاتِ أدواتِ القياسِ؛ مثلُ التذبذباتِ في قراءاتِ الأميترِ

 الرقميِّ عندَ استخدامِه في قياسِ التيارِ الكهربائيِّ في دارةٍ كهربائيّةٍ. وقدْ

 تنجمُ الأخطاءُ العشوائيّةُ.عنْ عواملَ تتعلّقُ بالبيئةِ المحيطةِ؛ مثلُ التباينِ

 في درجةِ حرارةِ المختبرِ في أثناءِ إجراءِ التجربةِ، أو الناجمةِ عن تكرارِ القياساتِ

 منَ الشخصِ الذي يقومُ بعمليّةِ القياسِ، إذْ عندَما يُعيدُ الشخصُ قياسَ

  كميّةٍ فيزيائيّةٍ ما مرّاتٍ عدّةٍ، فإنَّه في كلِّ مرّةٍ يحصلُ غالبًا على قياسٍ 

 مختلفٍ قليلاً عنِ الذي يسبقُه، مهما بلغتْ دقّةُ الأداةِ التي يستخدمُها.

 وتنجمُ الأخطاءُ العشوائيّةُ  أيضًا عنْ تقديرِ قراءةِ أداةِ القياسِ، ولاسيَّما

 في أدواتِ القياسِ المُدرَّجةِ،  إذْ لا ينطبقُ المؤشرُ أحيانًا على أحدِ تدريجاتِ

المقياسِ على نحوِ ما يظهرُ في الشكلِ ( 9)، ما يضطرُنا إلى تقديرِ قراءةِ

 المقياس.ومنْ مصادرِ الأخطاءِ العشوائيّةِ أيضًا، ما يُسمَّى بخطأِ

زاويةِ النظرِ Parallax error ، عندَ أخذِ القراءاتِ المختلفةِ منْ جهتينِ

 متناظرتينِ، على نحوِ ما يظهرُ في الشكلِ ( 10 )، إذْ يعتمدُ القياس

 الذي نحصلُ عليهِ على الزاويةِ التي ننظرُ منها إلى التقاءِ قاعدةِ

 المسطرةِ معَ حافةِ الورقةِ المرادِ قياسُ عرضِها. والأخطاءُ

 العشوائيّةُ تلازمُ أيَّ عمليّةِ قياسٍ، لكنْ يمكنُ التقليلُ من تأثيرِ هذهِ

 الأخطاءِ عنْ طريقِ تكرارِ القياساتِ مرّاتٍ عدّةٍ، وأخذِ الوسطِ الحسابيِّ

 لهذهِ القياساتِ.

الشكل ( 9): عدم انطباق المؤشر على

 أحد تدريجات المقياس

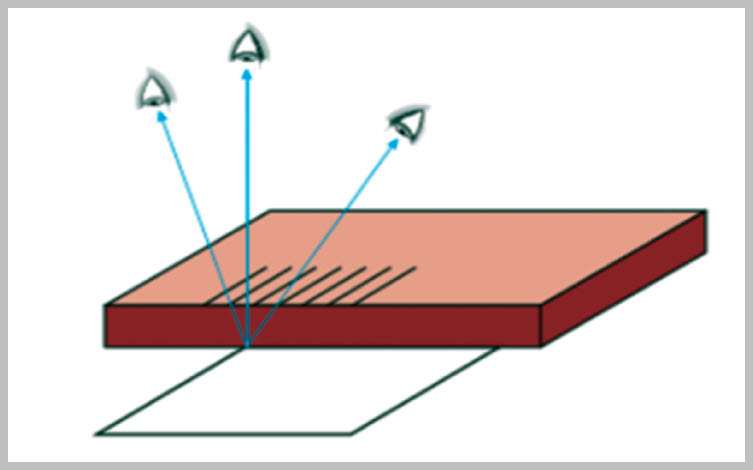
الشكل ( 10 ): النظرُ إلى المقياسِ من

زوايا مختلفةٍ يؤدي إلى خطأَ زاويةِ النظرٍ.

الأخطاءُ المنتَظمةُ Systematic Errors

هي الأخطاءُ التي تؤثرُ في القياساتِ جميعِها بالمقدارِ نفسِه وباتجاهٍ واحدٍ، بحيث

 تكونَ هذهِ القياساتُ أكبرَ منَ القيمةِ الحقيقيّةِ أو أصغرَ منها، لذا فهي أكثرُ

 قابليّةً للتنبُّؤِ منَ الأخطاءِ العشوائيّةِ. ومنْ مصادرِ الأخطاءِ المنتظمةِ، ما

 يُعرفُ بالخطأِ الصفريِّ Zero Error ، الذي ينجمُ عنْ عدمِ معايرةِ أدواتِ القياسِ

 الرقميّةِ، أو ذاتِ التدريجِ التناظريِّ على الصفرِ قبلَ استخدامِها، على نحوِ ما

 يظهرُ في الشكلِ ( 11 /أ، ب) على الترتيبِ، أو استخدامِ مسطرةٍ طرفُها تالفٌ

 مثلً، على نحوِ ما يظهرُ في الشكلِ ( 11 /ج) ، ما لم تُستخدمُ هذهِ المسطرةُ

في إجراءِ قياساتٍ بينَ جزأينِ لا يشتملانِ على الصفرِ. وقد ينشأُ الخطأُ المنتَظمُ

أيضًا عندَما لا تُضبطُ المُتغيّراتُ جميعُها التي تؤثّرُ في نتائجِ تجربةٍ ما، مثلُ قياسِ

 المجالِ المغناطيسيِّ الناشئِ عن مغناطيسٍ دونَ الأخذِ في الحسبانِ المجالَ

المغناطيسيَّ الناشئَ عنِ الأرضِ. ويمكنُ أنْ يكونَ خطأُ زاويةِ النظرِ منْ مصادرِ

الأخطاءِ المنتَظمةِ عندَما تُؤخذُ القراءاتُ جميعُها منَ الموقعِ نفسِه.

 يُشارُ إلى أنَّ تكرارَ القياساتِ لا يقلّلُ منْ تأثيرِ الأخطاءِ المنتَظمةِ كما هو الحال

 للأخطاء العشوائيّةِ، لكنْ يمكنُ التقليلُ منَ الأخطاءِ
المُنتَظمةِ من خلالِ الضبطِ الدقيقِ للإجراءاتِ المُتَّبعَةِ.

الشكل ( 11 ):
أ . مقياسٌ رقميٌّ.
ب. مقياسٌ ذو تدريجٍ تناظريِّ.
ج. مسطرةٌ طرفُها تالفٌ.

مثال محلول

أُحدّدُ نوعَ الخطأِ في كلٍّ ممّا يأتي مبيّنًا السببَ.

1 . في تجربةٍ لقياسِ تسارعِ الجاذبيةِ الأرضيةِ لم يُؤخذْ في الحسبانِ مقاومةُ الهواءِ.

2 . عملَ خالدٌ مخلوطًا حراريًّا في إناءٍ غيرِ معزولٍ.

3 . استخدمَتْ منى مِسطرتَها الخشبيّةَ الجديدةَ في قياسِ طولِ قلمِ الرصاصِ.

4 . كانَ أحمدُ يأخذُ قراءةَ ميزانِ الحرارةِ الزئبقيِّ المثبّتِ عموديًّا في إناءِ التسخينِ كلَّ

 خمسِ دقائقَ وهو جالسُ في مكانِه

الحلُّ:
 1 . منتَظمٌ؛ لأنَّ مقاومةَ الهواءِ تُعيقُ دائمًا حركةَ الأجسامِ، فهي تؤثرُ باتجاهٍ

    واحدٍ في نتائجِ التجربةِ.

 2 . منتَظمٌ؛ لأنَّ الإناءَ غيرَ المعزولِ يتبادلُ الحرارةَ معَ المحيطِ الخارجيِّ،

  فتتأثّرُ درجةُ حرارةِ المخلوطِ النهائيّةِ بالمحيطِ الخارجيِّ زيادةً أو نقصانًا

 (تبعًا لدرجةِ حرارةِ المخلوطِ مقارنةً بدرجةِ حرارةِ المحيطِ)، أيْ باتجاهٍ واحدٍ). 

 3 . عشوائيٌّ؛ لأنَّ القياسَ الذي تحصلُ عليهِ يمكنُ أن يكونَ أكبرَ أو أصغرَ

  منَ الطولِ الحقيقيِّ للقلمِ.  يمكنُ أن تقعَ مُنى في خطأٍ منتَظمٍ، إضافةً إلى

 الخطأِ العشوائيِّ، إذا لم تضبطْ مثلاً أحدَ طرفي القلمِ على صفرِ المسطرةِ).

4 . يقعُ أحمدُ في خطأٍ عشوائيٍّ إذا كانَ مستوى نظرِه منطبقًا دائمًا معَ

  مستوى الزئبقِ في ميزانِ الحرارةِ، ويقعُ في خطأٍ منتَظمٍ إذا كان مستوى

 نظرِه يصنعُ زاويةً معَ مستوى الزئبقِ في ميزانِ الحرارةِ، وكانتْ زاويةُ النظرِ ثابتةً.

تمرين

طلبتِ المعلمةُ من كلٍّ منْ سارةَ وسلمى استخدامَ مسطرتِها في قياسِ

طولِ كتابِ الفيزياءِ أربعَ مراتٍ متتاليةٍ، فحصلتْ كلٌّ منهما على القياساتِ

 الآتيةِ:

سارة: $27.5 , 27.4 , 27.5 , 27.2$

سلمى: $28.1 , 27.8 , 27.9 , 28.$

أَذكرُ نوعَ الخطأِ التجريبيِّ الذي وقعتْ فيهِ كلٌّ من سارةَ وسلمى،

وأُبيّنُ السببَ (علمًا أنَّ طولَ كتابِ الفيزياءِ يساوي 28.0cm ).

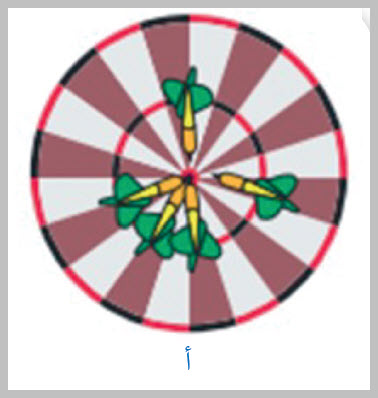
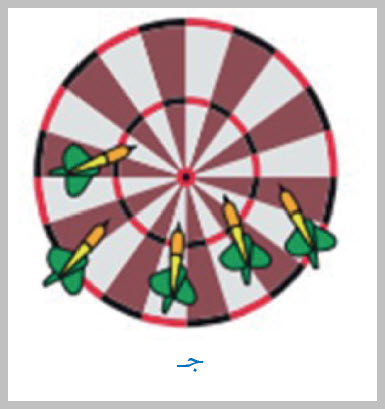
الدقّةُ والضبطُ Accuracy and Precision
تصفُ دقّةُ القياسِ مدى اقترابِ القيمةِ المقاسة منَ القيمةِ الحقيقيّةِ

 للكميّةِ الفيزيائيّةِ. والقيمُ الحقيقيّةُ للكميّاتِ الفيزيائيّةِ لا يمكنُ معرفتُها

تمامًا بسببِ أخطاءِ القياسِ، لكنْ توجَدُ قيمٌ مقبولةٌ متعارَفٌ عليها وهي

  مُعتمَدةٌ بوصفِها قيمًا حقيقيّةً تحتَ ظروفٍ معيَّنةٍ. فمثلاً، متوسطُ

 تسارعِ الجاذبيّةِ الأرضيّةِ (g) بالقربِ من سطحِ الأرضِ يساوي ($9.81m/s^2$)،

 وهذهِ القيمةُ مقبولةٌ ومعتَمدةٌ لتسارعِ الجاذبيّةِ الأرضيّةِ تحتَ الظروفِ 

 نفسِها. فإذا صَمّمتُ تجربةً لقياسِ تسارعِ الجاذبيّةِ الأرضيّةِ وحَصَلْتُ 

 على قيمةٍ قريبةٍ منَ القيمةِ المقبولةِ، مثلً( 9.80 ) في ظروفٍ مشابهةٍ، 

 فإنَّ هذهِ القيمةَ تُعَدُّ دقيقةً Accurate. أمّا الضبطُ Precision ،

 فهو يُظهِرُ مدى التوافقِ (الاتساقِ) بينَ القياساتِ عندَ تكرارِها تحتَ

 الظروفِ نفسِها.فعندَما أُكرّرُ قياسَ عرضِ كتابِ الفيزياءِ ثلاثَ مرّاتٍ مثلاً،

 وأحصلُ على القياساتِ  $(20.9 cm, 21.1 cm, 21.2 cm)$ ، فإنَّ هذهِ القياساتِ

 تُعَدُّ مضبوطةً؛ لأنَّها متقاربةٌ فيما بينَها،فالفرقُ بينَ أكبرِ قياسٍ (21.2)

وأصغرِ قياسٍ (20.9) يساوي ($0.3 cm$)، وهو مقدارٌ صغيرٌ بالنسبةِ إلى

طولِ الكتابِ، وهذا يدلُّ على أنَّ القياساتِ متقاربةٌ، وبوجهٍ عامٍّ، كلّما قلَّ

 الفرقُبينَ أكبرِ قياسٍ وأصغرٍ قياسٍ كانَ القياسُ أكثرَ ضبطًا. ولنفترضْ

 أنَّ القيمةَ المقبولةَ لعرضِالكتابِ تساوي ( $21.0 cm$)،فإنَّ هذهِ القياساتِ

 تتّسمُ أيضًا بالدقّةِ لقربِها منَ القيمةِ المقبولةِ.لكنْ قد تكونُ القياساتُ

دقيقةً وغيرَ مضبوطةٍ (قليلةَ الضبطِ)، أو مضبوطةً وغيرَ دقيقةٍ.

 والشكلُ ( 12 ) يلخصُ بعضَ هذهِ الحالاتِ، حيثُ تمثّلُ البقعةُ الحمراءُ

 (مركزُ الهدفِ) القيمةَ المقبولةَ.يعتمدُ ضبطُ القياساتِ اعتمادًا رئيسًا على

 دقّةِ أدواتِ القياسِ المُستخدَمةِ، فمثلاً،بمقارنةِ المسطرةِ بالقَدمةِ ذاتِ

 الوَرْنيَّةِ أو الميكروميتر، نجدُ أنَّ الميكروميتر أكبرُهنَّ ضبطًا، لأنَّهُ يقيسُ لأقربِ

($0.01 mm$)،تليهِ القَدَمةُ ذاتُ الوَرْنيةِ، إذْ تقيسُ لأقربِ ( $0.1mm$ )، في حينِ أنَّ

 المِسطرةَ تقيسُ لأقربِ ( $1mm$ )، فكلّما زادَ عددُ المنازلِ العشريّةِ التي تقرؤُها

 الأداةُ زادَ ضبطُ القياسِ، وقلَّ في المقابلِ ما يُسمَّى بعدمِ اليقينِ (الشكِّ).

 وأنَّ الشخصَ الذي يتّبعُ المنهجَ العلميَّ في القياسِ أو التجريبِ يحصلُ على

  قياساتٍ أكثرَ دقّةً منَ الشخصِ الأقلِّ التزامًا بهذا المنهجِ.

الشكل ( 12 ):
أ . قياساتٌ دقيقةٌ ومضبوطةٌ.
ب. قياساتٌ مضبوطةٌ وغيرُ دقيقةٍ.
ج. قياساتٌ غيرُ دقيقةٍ وغيرُ مضبوطةٍ

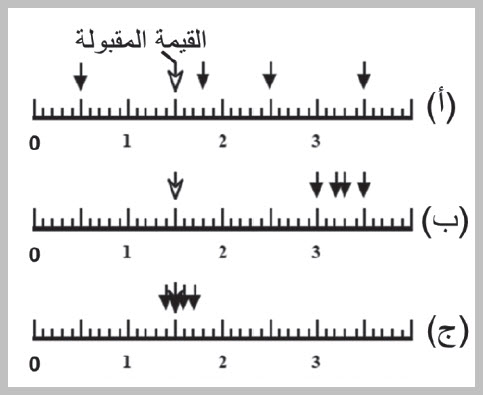
مثال محلول 

يبيّنُ الشكلُ قياساتٍ لقُطرِ حلقةٍ فِلزيّةٍ قامَ بها ثلاثةُ طلاب (أ، ب، ج)،

حيثُ كرّرَ كلٌّ منهم القياسَ أربعَ مرّاتٍ متتاليةٍ، وهي مُمثَّلةٌ بالأسهمِ.

أَصفُ قياساتِ الطلابِ الثلاثِة من حيثُ الدقّةُ والضبطُ، علمًا بأنَّ القيمةَ

المقبولةَ لقُطرِ الحلقةِ يساوي (1.5 cm).

الحلُّ:
أُلاحظُ منَ الشكلِ أنَّ قياساتِ الطالبِ (أ):      $cm$(3.5 ,2.5. 1.8, 0.5)   على الترتيبِ،

وهي بعيدةٌ عنِ القيمةِ المقبولةِ باستثناءِ القياسِ ( 1.8cm)، لذا فهي غيرُ دقيقةٍ.

وهي متباعدةٌ أيضًا بعضُها عنْ بعضٍ (غيرُ متّسقةٍ)، لذا فهي غيرُ مضبوطةٍ. أمّا

قياساتُ الطالبِ (ب):  $cm$(3.0 , 3.2 , 3.3 , 3.5 )  على الترتيبِ، فهي بعيدةٌ عنِ

القيمةِ المقبولةِ، لذا فهي غيرُ دقيقةٍ، ولكنَّها متقاربةٌ بعضُها من بعضٍ (متّسقةٌ)،

لذا فهي مضبوطةٌ. في حينِ أنَّ قياساتِ الطالبِ(ج): (1.7 , 1.6 , 1.5 , 1.4) على الترتيبِ،

فهي قريبةٌ منَ القيمةِ المقبولةِ، ومتّسقةٌ فيما بينَها، لذا فهي دقيقةٌ ومضبوطةٌ

الخطأُ المطلقُ والخطأُ النسبيُّ Absolute Error and Relative Error

يُعرّفُ الخطأُ المطلقُ Absolute Error بأنَّهُ: الفرقُ المطلقُ بينَ القيمةِ المقاسة

 والقيمةِ الحقيقيّةِ (المقبولةِ). أيْ إنَّ:

  الخطأَ المطلقَ = |القيمةَ المقاسة– القيمةِ المقبولةِ|

     ويُلاحَظُ منَ المعادلةِ السابقةِ أنَّهُ كلّما كانَ الفرقُ بينَ القيمةِ المقاسةِ

    والقيمةِ المقبولةِ  صغيرًا كانَ الخطأُ المطلقُ صغيرًا، ولمّا كانتْ دقّةُ

     القياسِ ترتبطُ بمدى اقترابِ القيمةِ المقاسةِ منَ القيمةِ المقبولةِ، فإنَّهُ

     كلّما قلَّ الفرقُ بينَ القيمة المقاسة والقيمة المقبولةزادتْ دقّةُ القياسِ،

    أيْ كلّما قلَّ الخطأُ زادتْ دقّةُ القياسِ. أمّا الخطأُ النسبيُّ Relative Error فهو:

  النسبةُ بينَ الخطأِ المطلقِ والقيمةِ الحقيقيّةِ (المقبولةِ). أيْ إنَّ:

 وللحصولِ على نسبةٍ مئويةٍ للخطأِ نضربُ المعادلةَ السابقةَ في: % 100 ، 

 ويُطلقُ على الناتجِ اسمَالخطأِ النسبيِّ المئويِّ Percentage Error . أيْ إنَّ:

ولحسابِ الخطأِ المطلقِ أو الخطأِ النسبيِّ لأيِّ عمليةِ قياسٍ فإنَّهُ يجبُ معرفةُ

 القيمةِ المقبولةِ، أمّا إذا كانتِ القيمةُ المقبولةُ غيرَ معروفةٍ، فلا بدَّ من تكرارِ

 القياساتِ، ثمَّ حسابِ المتوسطِ الحسابيِّ Mean لهذهِ القياساتِ. ويُحسَبُ

المتوسطُ الحسابيُّ بجمعِ القياساتِ جميعِها، ثمَّ قسمةِ الناتجِ على عددِ هذهِ

 القياساتِ، أيْ إنَّ:

  ويكونُ المتوسطُ الحسابيُّ في هذهِ الحالةِ ممثلاً للقيمةِ المقبولةِ. وإذا كانتْ

 قياساتُنا مضبوطةً، أيْ كانتِ الأدواتُ المستخدمةُ دقيقةً  (عددُ المنازلِ العشريّةِ

 التي تعطيها هذهِ الأدواتُ كبيراً نسبيًّا)، وكانتِ الإجراءاتُ المُتَّبعةُ في القياسِ

 منضبطةً، كانَ المتوسطُ الحسابيُّ قريبًا جدًّا منَ القيمةِ المقبولةِ، فنعُدُّه مساويًا

 لها، أيْ إنَّ:

 القيمةَ المقبولةَ = المتوسطَ الحسابيَّ

أرادَ عليٌّ أنْ يتأكدَ من أنَّ حجمَ كميّةِ ماءِ الشربِ الموجودةِ في إحدى العبوّاتِ

البلاستيكيةِ تساوي (20mL) )، على نحوِ ما هو مكتوبٌ عليها. فاستخدمَ

 المخبارَ المدرّجَ، وأفرغَ محتوياتِ العبوّةِ في المخبارِ مباشرةً دونَ الأخذِ في

 الحسبانِ ضيقَ فوهّتِه، ما أدّى إلى انسكابِ كميّةٍ بسيطةٍ منَ الماءِ خارجَ المخبارِ،

  فكانَ حجمُ الماءِ الذي قاسَه عليٌّ ( 190mL ). أُجيبُ عمّا يأتي:

      1 . أَحسُبُ ك منَ: الخطأِ المطلَقِ، الخطأِ النسبيِّ، الخطأِ النسبيِّ المئويِّ في

          قياسِ عليٍّ.

      2 . أُبيّنُ نوعَ الخطأِ الذي وقعَ فيهِ عليٌّ عندَما سكبَ الماءَ في المخبارِ المُعطياتُ:

           القيمةُ المقبولةُ لحجمِ الماءِ = $200mL$

            القيمةُ المقاسة = $190mL$
     المطلوبُ: الخطأُ المطلقُ، الخطأُ النسبيُّ، الخطأُ النسبيُّ المئويُّ، نوعُ الخطأِ.

     الحلُّ:
        1 . الخطأُ المطلقُ = | القيمة المقاسة - القيمة المقبولة |

                            $10 ml = | 200 – 190 |=$

$\mathrm{الخطأ} \mathrm{النسبي} = \frac{\mathrm{الخطأ} \mathrm{المطلق}}{\mathrm{القيمة} \mathrm{المقبولة} }= \frac{10}{200}= 0.05$
$$\begin{gathered} \mathrm{الخطأُ} \mathrm{النسبيُّ} \mathrm{المئويُّ} = \mathrm{الخطأَ} \mathrm{النسبيَّ} \times \%100 \\ = 0.05 \times \%100= \% 5 \end{gathered}$$
2 . نوعُ الخطأِ الذي وقعَ فيهِ عليٌّ كانَ منتَظمًا، لأنَّه لو أعادَ قياسَ حجمِ الماءِ

    مرّةً بعدَ مرّةٍ،  لحصلَ دائمًا على قياسٍ أقلَّ منَ القيمةِ المقبولةِ ( $200 ml$)؛

     لأنَّ كميّةً منَ الماءِ قد فُقِدتْ في أثناءِ إفراغِ محتوى العبوّةِ في المخبارِ المدرّجِ.

تمرين 

في تجربةٍ قامتْ بها بيانُ لقياسِ المقاومةِ الكهربائيّةِ لسلكٍ فلزيٍّ عمليًّا،

توصَّلتْ إلى أنَّ مقاومةَ السلكِ تساوي ( 0.6 ) أوم بخطأٍ نسبيٍّ مئويٍّ

مقداره (4%) .أَحسُبُ كلاً منَ الخطأِ المطلقِ في قياسِ المقاومةِ والقيمةِ

المقبولةِ لمقاومةِ السلكِ.