اتحقق من فهمي
- صفحة 9
أحدد إذا كان كل مما يأتي كثير حدود أم لا. وفي حال كان كثير حدود أكتبه بالصورة القياسية، ثم أحدد المعامل الرئيس، والدرجة ، والحد الثابت :
|
الحد الثابت |
المعامل الرئيس |
الصورة القياسية |
درجة كثير الحدود |
كثير الحدود |
الفرع والمسألة |
|
9 |
H(x) = x5 -5x + 9 |
5 |
✔️
|
A ) h(x)= 9 -5x + x5
|
|
|
✘ |
✘ |
✘ |
✘ |
✘ |
B ) F(x) = + 2x
|
|
0 |
-2 |
G(x) = -2x4+18 x3 – 54 x2 +54 x |
4 |
✔️
|
C ) G(x) = 2x( 3 -x )3
|
|
-7 |
R(x) = -7 x5 + + |
5 |
✔️
|
D ) r(x) = - 7x5 + |
توضيح فرع c
G(x) = 2x( 3 -x )3
= 2x ( 27 -27 x + 9 x2 - x3 )
= 54 x – 54 x2 + 18 x3 – 2 x4
ومن ثم نرتبها على الصورة القياسية
- صفحة11
أمثل بيانيا كل اقتران مما يأتي ، محددا مجاله و مداه :
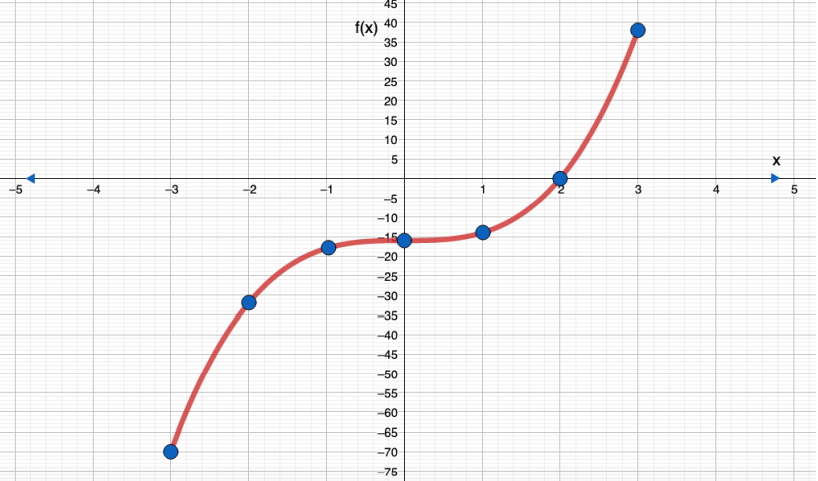
- F (x) = 2 x3 - 16 , -3 ≤ x ≤ 3
الحل :
|
X |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
F(x) |
-70 |
-32 |
-18 |
-16 |
-14 |
0 |
38 |
المجال
المدى
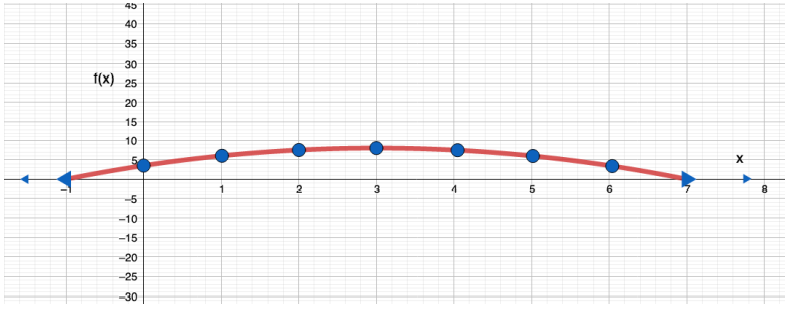
- F(x) = - 0.5 x2 +3x + 3.5
الحل :
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
F(x) |
6 |
8 |
6 |
المجال مجموعة الأعداد الحقيقية
المدى
صفحة12
- إذا كان, g(x) = -4x3 + 6x2 - 5 f(x) = 3x2 + 8x3 +2x +13فأجد f(x) + g(x)
الحل
F(x) + g(x) = 3x2 + 8x3 +2x +13 + -4x3 + 6x2 - 5
= 9 x2 +4 x3 +2x +8
2. إذا كان f(x) = 5x3 -12x2 + 3x +20 , g(x) = x3 + 6x2 - 14 فأجد g(x) – f(x)
الحل
g(x) – f(x) = x3 + 6x2 - 14 – ( 5x3 -12x2 + 3x +20)
= x3 + 6x2 - 14 + - 5x3 +12x2 - 3x - 20
= -4 x3 + 18x2 - 3x – 34
- صفحة13
أجد ناتج ضرب f(x) , g(x) في كل مما يأتي :
- f(x) = 5x2 + 4 , g(x) = 7x +6
الحل
f(x). g(x) = ( 5x2 + 4 ) . ( 7x +6)
= 35 x3 + 30 x2 + 28x +24
- f(x) = 2x3 + x – 8 , g(x) = 5 x2 +4x
الحل
f(x) . g(x) = ( 2x3 + x – 8 ) . ( 5 x2 +4x)
= 10 x5 + 8 x4 + 5 x3 +4 x2 -40 x2 -32
= 10 x5 + 8 x4 + 5 x3 - 36 x2 -32x
صفحة 15
يمثّلُ الاقترانُ موقعَ جسمِ يتحرّكُ في مسارٍ مستقیمِ، حیثُ s موقعُ الجسمِ بالأمتارِ بعدَ ٤ ثانيةً.
a) أحدّدُ موقعَ الجسمِ لحظةَ بدءِ الحركةِ.
b) أحدّدُ موقعَ الجسمِ بعدَ 3 ثوانٍ منْ بدءِ الحركةِ.
c) متى يكونُ الجسمُ عندَ نقطةِ الأصلِ؟
d) هل يعودُ الجسمُ إلى النقطةِ التي بدأَ الحركةَ منها؟

أتدرب و أحل المسائل صفحة 15
- أحدد إذا كان كل مما يأتي كثير حدود أم لا . وفي حال كان كثير حدود أكتبه بالصورة القياسية ، ثم أحدد المعامل الرئيس، والدرجة ، والحد الثابت :
|
الحد الثابت |
المعامل الرئيس |
الصورة القياسية |
درجة كثير الحدود |
كثير الحدود |
الفرع والمسألة |
|
4 |
-1 |
f(x) = – x+4 |
1 |
✔️
|
|
|
✘ |
✘ |
✘ |
✘ |
✘ |
|
|
-12 |
12 |
H(x) = 12 x2 -19x -12 |
2 |
✔️
|
|
|
0 |
5.3 |
l(x) = 5.3 x3 + 3x2 – 2x |
3 |
✔️
|
|
|
0 |
-16 |
J(t) = -16 t2 + t |
2 |
|
|
|
✘ |
✘ |
✘ |
✘ |
✘ |
|
|
✘ |
✘ |
✘ |
✘ |
✘ |
|
|
0 |
1 |
F(y) = y7 – 8 y5 +16 y3 |
7 |
✔️ |
|
توضيح فرع 3
H(x) = 3x( 4x- 7) +2x -12
= 12 x2 – 21 x +2x -12
= 12 x2 - 19 x - 12
توضيح فرع 8
F(y) = y3 ( 4 – y2 )2
= y3 ( 16 – 8 y2 + y4 )
= 16 y3 – 8 y5 + y7
- أمثل كل اقتران مما يأتي بيانيا ، محددا مجاله ومداه :
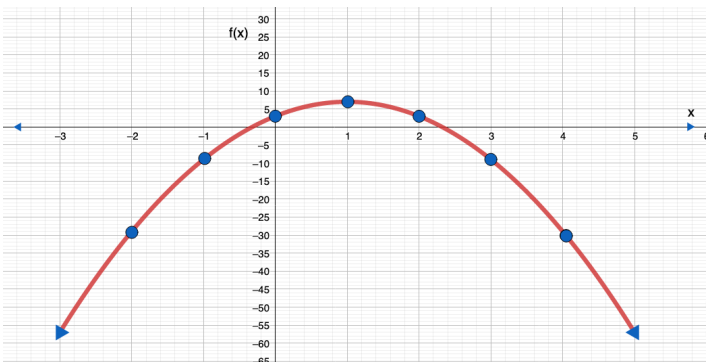
9) f(x) = x2 -3x - 4
|
X |
1- |
0 |
1 |
2 |
3 |
4 |
|
|
F(x) |
0 |
4- |
6- |
6- |
4- |
0 |
المجال : مجموعة الأعداد الحقيقية
المدى :
10) f(x) = -4 x2 + 8x +3
|
X |
2- |
1- |
0 |
1 |
2 |
3 |
4 |
|
F(x) |
29- |
9- |
3 |
7 |
3 |
9- |
29- |
المجال : مجموعة الأعداد الحقيقية
المدى :
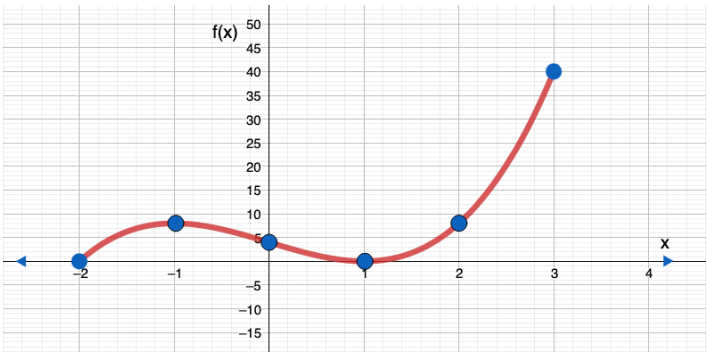
11) y = 2x3 - 6x + 4 , -2 ≤ x ≤ 3
|
X |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
F(x) |
0 |
8 |
4 |
0 |
8 |
40 |
المجال : [ -2 , 3 ]
المدى : [ 0 , 40]
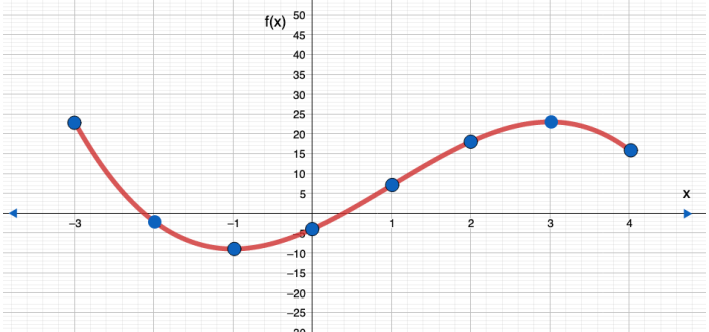
12) y = 3x2 - x3 + 9x – 4 , -3 ≤ x ≤ 4
|
X |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
F(x) |
23 |
-2 |
-9 |
-4 |
7 |
18 |
23 |
16 |
المجال : [ -3 , 4 ]
المدى : [ -9 , 23]
- إذا كان f(x) = 2x +1 , g(x) = 5 x2 – 2x3 +4 , h(x) = x4 – 5x2 +3x – 6 فأجد كل مما يأتي بالصورة القياسية :
13) h(x) + g(x) = x4 – 5x2 +3x – 6 +5 x2 – 2x3 +4
= x4 – 2x3 + 3x – 2
14) g(x) – h(x) = 5 x2 – 2x3 +4 – ( x4 – 5x2 +3x – 6)
= 5 x2 – 2x3 +4 – x4 + 5x2 -3x +6
= –x4 – 2x3 + 10 x2 - 3x +10
15) f(x) . h (x) = ( 2x +1 ) . ( x4 – 5x2 +3x – 6)
= ( 2x5 -10 x3 + 6x2 – 12 x) + ( x4 – 5x2 +3x – 6)
= 2x5 + x4 -10 x3 +x2 – 9 x – 6
16) x( f(x)) + h(x) = x ( 2x +1) + x4 – 5x2 +3x – 6
= 2 x2 + x + x4 – 5x2 +3x – 6
= x4 – 3x2 +4x – 6
17) ( f(x))2 – g(x) = (2x +1)2 - ( 5 x2 – 2x3 +4)
= (4 x2 + 4x +1 ) -5 x2 + 2x3 – 4
= 2x3 - x2 + 4x – 3
18) h(x) – x (g(x)) = x4 – 5x2 +3x – 6 – x( 5 x2 – 2x3 +4)
= x4 – 5x2 +3x – 6 –5x3 + 2x4 - 4x
= 3x4 –5x3 – 5x2 - x – 6
يُمثّلُّ الاقترانُ موقعَ جسمٍ يتحرّكُ في مسارٍ مستقيمٍ، حيثُ s موقعُ الجسمِ بالأمتارِ بعدَ ٤ ثانيةً.
19) أحدّدُ موقعَ الجسمِ لحظةَ بدءِ الحرکةِ.
20) أحدّدُ موقعَ الجسمِ بعدَ 4 ثوانٍ منْ بدءِ الحرکةِ.
21) متى يكونُ الجسمُ عندَ نقطةِ الأصلِ؟ بعد 3 ثوانٍ من بدء الحركة.
22) هلْ يعودُ الجسمُ إلى النقطةِ التي بدأَ الحركةَ منها؟ نعم، يعود إليها بعد ثانية واحدة من بدء الحركة، وبعد ثانيتين من بدء الحركة.
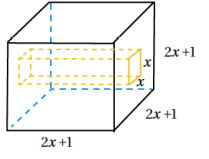
23) هندسة : مكعب من الخشب، طول ضلعه (2x+1)cm حفر فيه تجويف مقطعة مربع طول ضلعه x cm ، وهو يمتد من أحد الأوجه الى الوجه المقابل. أكتب بالصورة القياسية الاقتران الذي يمثل حجم الجزء المتبقي من المكعب.
الحل
V = (2x +1)3 – x2 ( 2x+1)
V = 8x3 +12x2 +6x +1 – 2x3 – x2
V = 6x3 +11x2 +6x +1
24) ينتج مصنع ثريات عددها x ثريا أسبوعيا، حيث 350 ≤ x ≤ 0 ، و بيبع الواحدة منها بسعر( 150 – 0.3 x) دينارا. إذا كانت تكلفة إنتاج x من الثريات هي ( 6300 +60x -0.1 x2 ) دينارا فأجد ربح المصنع من إنتاج x ثريا أسبوعيا وبيعها .
P(x) = x (150 – 0.3 x) - ( 6300 +60x - 0.1 x2 )
P(x) = 150x – 0.3 x2 - 6300 - 60x +0.1 x2
P(x) = – 0.2 x2 + 90x - 6300
مهارات التفكير العليا
تبريرٌ: يظهرُ في الشكلِ المجاورِ منحنى اقترانِ الموقع لجسم يتحركُ في مسارمستقيمِ، حيثُ s الموقعُ بالأمتارِ وا الزمنُ بالثواني. أستعملُ الشكلَ للإجابةِ عنِ الأسئلةِ الآتيةِ مبرِّرًا إجابتي:
25) ما الفترةُ (الفتراتُ) الزمنيَّةُ التي يكونُ فيها الجسمُ في الجهةِ الموجبةِ منْ نقطةِ الأصلِ؟
26) أحدّدُ الموقعَ الابتدائيَّ للجسمِ.
27) ما أبعدُ موقع للجسمِ عن نقطةِ الأصلِ وهو في الجهة السالبة منها؟
الحل :
25)
26)
27)
28) مسألة مفتوحة : اكتب كثيري حدود، أحدهما ذو حدين، و الآخر ثلاثي الحدود، بحيث يكون ناتج ضربهما اقترانا ذا حدين.
الحل :
( x2 – x) ( x2 + x +1 )
29) تحد : أجد أصفار الاقتران : f(x) = x3 – x2 – 4x +4
الحل
F(x) = x2 ( x – 1) – 4 ( x – 1)
F(x) = x2 – 4 ( x – 1)
F(x) = (x-2) ( x +2 ) ( x – 1)
F(x) = 0
X = 2 , -2 , 1
30) تبرير : إذا كان f , g كثيري حدود ، فاكتب العلاقة بين درجة كل منهما ودرجة كثير الحدود h الناتج من جمعهما وطرحهما وضربهما مبرر إجابتي .
الحل
ليكن f من الدرجة n
ليكن g من الدرجة m
H = f + g من الدرجة ( القيمة الأكبر من n , m )
H =f – g من الدرجة ( القيمة الأكبر من n , m )
لأنه في الجمع والطرح نجمع الحدود المتشابهة
H= f . g من الدرجة ( n + m)
الضرب لأن الأسس تجمع في حالة الضرب
و بمعنى آخر :
إذا كانت درجة f أكبر من درجة g فإن ناتج الأكبر (F)
أما إذا كانت درجة f مساوية لدرجة g فإن درجة جمعهما أو طرحهما مساوية لدرجة f أو أقل منها في حالة كان المعاملات لأعلى درجة متساويين في المقدار و مختلفات في الإشارة
كتاب التمارين
أحدد إذا كان كل مما يأتي كثير حدود أم لا، محددا الدرجة والمعامل الرئيس والحد الثابت لكل كثير حدود ، ثم أكتبه بالصورة القياسية
|
الحد الثابت |
المعامل الرئيس |
الصورة القياسية |
درجة كثير الحدود |
كثير الحدود |
الفرع والمسألة |
|
✘ |
✘ |
✘ |
✘ |
✘ |
|
|
-1 |
-5 |
3 |
✔️
|
|
|
|
1 |
✔️
|
|
|||
|
✘ |
✘ |
✘ |
✘ |
✘ |
4. |
أمثل بيانيا كلا مما يأتي ، محددا مجاله ومداه :
5. f(x) = 2x3 - 5 ,
المجال [ -2 , 3] ، المدى [ -21 , 49]
|
X |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
F(x) |
-21 |
-7 |
-5 |
-3 |
11 |
49 |
_1645116661.png)
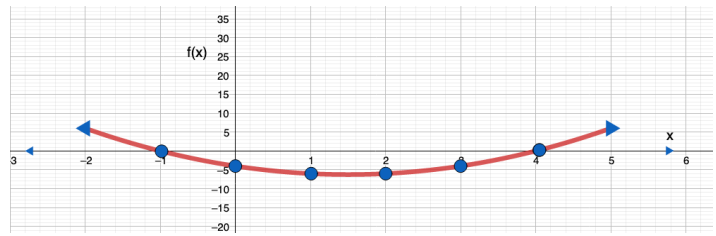
6.
المجال [ -2 , 2] ، المدى[ 3 , 19]
|
X |
-2 |
-1 |
0 |
1 |
2 |
|
F(x) |
19 |
7.5 |
5 |
5.5 |
3 |
_1645116919.png)
7. g(x) = 12 - 4x - x2
= -x2 - 4x + 12
: المجال : مجموعة الأعداد الحقيقية المدى
|
X |
-4 |
-3 |
-2 |
0 |
1 |
|
F(x) |
12 |
15 |
16 |
12 |
7 |
_1645113548.png)
8. h(x) = ( 2x -5)2 -10
= 4x2 - 20x + 25 -10
= 4x2 - 20x +15
المجال مجموعة الأعداد الحقيقية المدى
|
X |
0 |
2 |
3 |
4 |
|
|
F(x) |
15 |
-9 |
-10 |
-9 |
-1 |
_1645113633.png)
إذا كان f(x) = 2x2 -4x3 +5x - 1 و g(x) = x3 +5x2 - 7 و h(x) = 2x - 4 فأجد ناتج ما يأتي :
9. f(x) +g(x) = (2x2 -4x3 +5x - 1 ) + (x3 +5x2 - 7)
= - 3x3 +7 x2 +5x -8
10. f(x) - g(x) = ( 2x2 -4x3 +5x - 1) - (x3 +5x2 - 7)
= -5x3 -3x2 +5x +6
11. g(x) - x(h(x)) = (x3 +5x2 - 7) - x(2x - 4)
= x3 +5x2 - 7 - ( 2x2 -4x)
= x3 +3x2 +4x -7
12. h(x) . f(x) = ( 2x - 4) .(2x2 -4x3 +5x - 1)
= -8x4 +20x3 +2x2 -22x +4
13. (h(x))2 +f(x) = (2x - 4 )2 + (2x2 -4x3 +5x - 1)
= ( 4x2 -16x +16) + 2x2 -4x3 +5x -1
= -4x3 +6x2 -11x +15
14. f(x). g(x) = (2x2 -4x3 +5x - 1) .( x3 +5x2 - 7)
= -18 x5 -4x6 +15x4 +52x3 -19x2 -35x +7
15. هل العدد صفر للاقتران h(x) = -x4 - 5x3 + 7x - 10 ؟ أبرر إجابتي
الحل :
نعم يعتبر صفر للاقتران h(x)
16. أجد أصفار الاقتران g(x) = ( x- 1)3 -3 ( x -1)2
الحل :
g(x) = 0
(x -1)2 .( x -1 -3) =0
(x -1 )2 .(x -4) = 0
هما أصفار الاقتران x = 1 , x= 4
يمثّلُ الاقترانُ موقعَ جسم يتحرّكُ في مسارٍ مستقيمٍ، حيثُ ؟ موقعُ الجسمِ بالأمتارِ بعدَ ٤ ثانيةً.
17 أحدّدُ موقعَ الجسمِ لحظةَ بدءِ الحركةِ.
18 أحدّدُ موقعَ الجسمِ بعدَ ثانيتينِ منْ بدءِ الحرکةِ.
19 متى يكونُ الجسمُ عندَ نقطةِ الأصلِ؟ بعد 10 ثوانٍ من بدء الحركة.
20 هل يعودُ الجسمُ إلى النقطةِ التي بدأَ الحركةَ منْها؟ يعود إلى النقطة التي بدأ الحركة منها بعد حوالي 0.26s وبعد حوالي 9.7s من بدء حركته.