الآحادُ وَالعَشَراتُ
تهيئة:
تعلمنا في الدرس السابق كيف أننا نستطيع جَمَعَ كُلَّ 10 واحِداتٍ لنحصل عَلى 1 عَشَرَةٍ.
مثال:
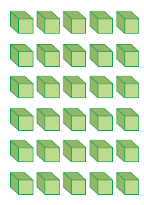
إذا كان معي مجموعة من المكعبات، فإنني أستطيع حصرها في عشرات، أي أنني أَجْمَعُ كُلَّ 10 واحِداتٍ لِأَحْصُلَ عَلى 1 عَشَرَةٍ.
الآن سأقوم بجمع كل 10 واحدات مع بعضها.
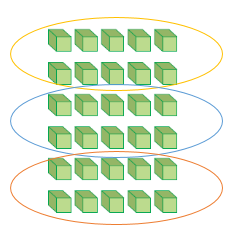
قمت بحصر كل 10 واحدات مع بعضها.
والآن سأقوم بجمعها في أعمدة، يمثل كل عامود منها 10 مكعبات.
يمثل كل عامود 10 مكعبات، أي أنّ 10 واحدات = 1 عشرة.
كَمْ عَشَرَةً في الشَّكْلِ؟
أقارِنُ إجابتي بالإجابة الآتية:
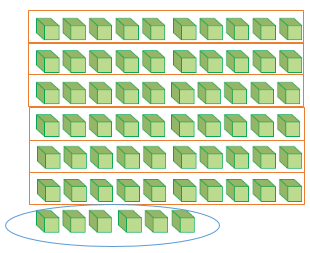
أستطيع معرفة عدد العشرات في الشكل السابق من خلال حصر كل 10 نجمات مع بعضها على النحو الآتي:
قمتُ بحصر 10 نجمات مع بعضها، ولكن ما تبقى لا يُساوي 10 لذلك لم أستطع حصرها في مجموعة واحدة.
لذا فإنّني أقول: يوجد 10 واحدة في الشكل، وتبقى معي 5 نجمات.


 الباقي يُكتب أولًا عند كتابة العَدد وَهو في المثال السابق (5)، أما عدد العشرات التي حصرتها فتكتب ثانيًا وتسمى العَشرات، وهي في المثال السابق (1)
الباقي يُكتب أولًا عند كتابة العَدد وَهو في المثال السابق (5)، أما عدد العشرات التي حصرتها فتكتب ثانيًا وتسمى العَشرات، وهي في المثال السابق (1)
ليكون العَدد الذي تشكل هُوَ (15)، (5) آحاد، (1) عَشرات.

أَتَأمل المثال الآتي:
أَجْمَعُ كُلَّ 10 واحِداتٍ لِأَحْصُلَ عَلى 1 عَشَرَةٍ، وَما تَبَقّى يُسَمّى آحادًا.
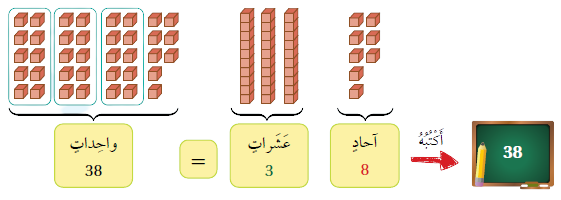

وأنّ الباقي أسميته آحادًا ووضعته في منزلة الآحاد.
 وعند كتابة العدد الذي حصلت عليه بعد كتابة الآحاد والعشرات، قمت بكتابة الآحاد أولًا وَهُوَ (8)، ثمّ قمت بكتابة عدد أعمدة العشرات ثانيًا، وكتبتها في منزلة العَشَرات وَهي (3) أعمدة، ليصبح العَدَد (38).
وعند كتابة العدد الذي حصلت عليه بعد كتابة الآحاد والعشرات، قمت بكتابة الآحاد أولًا وَهُوَ (8)، ثمّ قمت بكتابة عدد أعمدة العشرات ثانيًا، وكتبتها في منزلة العَشَرات وَهي (3) أعمدة، ليصبح العَدَد (38).
نَشاط (1)
أَجْمَعُ كُلَّ 10 واحِداتٍ لِأَحْصُلَ عَلى 1 عَشَرَةٍ، وَما تَبَقّى يُسَمّى آحادًا. ثُمَّ أكتب العَدد:
أقارِنُ إجابتي بالإجابة الآتية:
عَدد العَشَرات = 6
الباقي = 6
العَدد هُوَ: 66، حيث 6 آحاد وَ 6 عَشَرات.
أَتَحَدَّثُ: كَيْفَ أُحَدِّدُ عَدَدَ الآحادِ وَعَدَدَ الْعَشَراتِ في عَدَدٍ مِنَ الْمُكَعَّباتِ؟
أقارِنُ إجابتي بالإجابة الآتية:
أستطيع تَحديد عَدَدَ الآحادِ وَعَدَدَ الْعَشَراتِ في عَدَدٍ مِنَ الْمُكَعَّباتِ،
من خلال تحديد العَشرات وحصرها في مجموعة تمثل كل منها 10، وما تبقى يُسمى آحادًا، وأقوم بكتابة الآحاد أولًا ثُمّ العَشَرات.