|
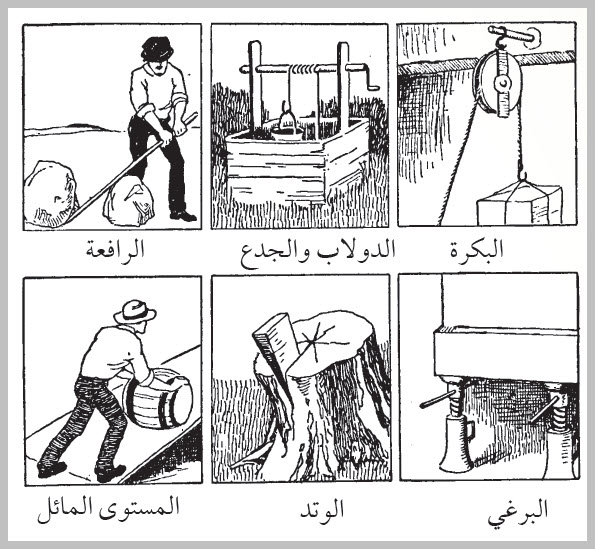
الآلات البسيطة نستخدمُ في حياتِنا كثيرًا منَ الآلاتِ التي تساعدُنا على إنجازِ أعمالِنا اليوميّةِ، منها البسيطةُ، مثلُ: المِقصُّ، والمِلقطُ، ومنها المُركبةُ، مثلُ: الدرّاجةِ، والسيارةِ، إذْ إنَّها تحتوي في مكوّناتِها على كثيرٍ منَ الآلاتِ البسيطةِ. والآلاتُ، سواءٌ أكانتْ تعملُ بمحركاتٍ أم بأشخاصٍ، فهي تُسهّلُ علينا إنجازَ أعمالِنا المختلفةِ. وسأتعرّفُ في هذا الدرسِ أنواعَ الآلاتِ البسيطةِ والآليّةِ التي تساعدُنا على إنجازِ أعمالِنا. الآلةُ البسيطةُ Simple Machine الآلةُ البسيطةُ هي أداةٌ تساعدُنا على إنجازِ الشغلِ بسهولةٍ. وذلكَ بتغييرِ مقدارِ القوةِ المؤثّرةِ في جسمٍ أو اتجاهِها، أو مقدارِ المسافةِ التي يتحرّكُها الجسمُ تحتَ تأثيرِ القوةِ (الإزاحةِ). ولذا تُصنَّفُ الآلاتُ البسيطةُ بناءً على ذلكَ إلى ستةِ أنواعٍ رئيسةٍ، ملخَّصةٍ في الشكلِ ( 6).والآلةُ البسيطةُ لا تقلّلُ منَ الشغلِ المبذولِ، وإنما تُسهِّلُ إنجازَهُ.
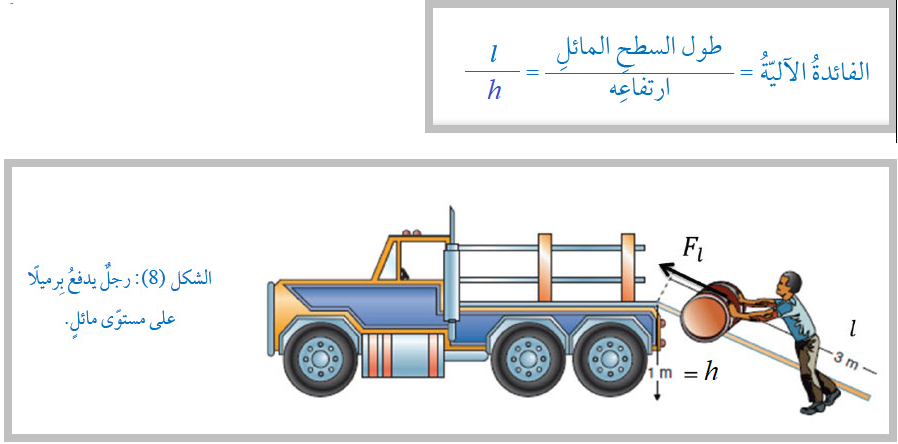
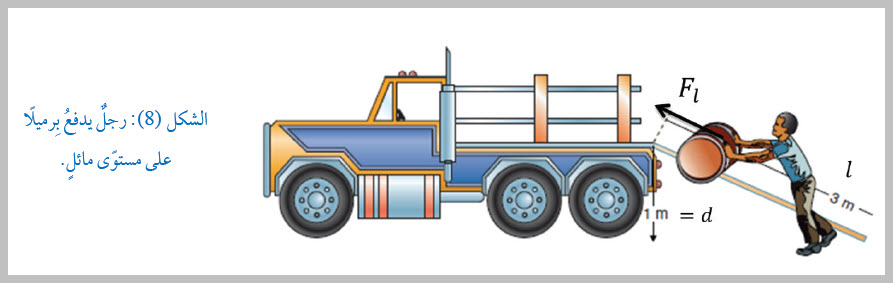
الشكل ( 6): أنواع الآلات البسيطة. المستوى المائلُ Inclined Plane أنواعِ الآلاتِ البسيطةِ. ويعملُ المستوى المائلُ على تقليلِ القوةِ اللازمةِ لإنجازِ الشغلِ نفسِه المطلوبِ إنجازُه دونَ استخدامِ المستوى المائلِ، ففي الشكلِ (8)، وعلى افتراضِ أنَّ وزنَ البِرميلِ (Fg = 1200N)، فإنَّ القوةَ (F) اللازمةَ لرفعِ البرميلِ رأسيًّا بسرعةٍ ثابتةٍ دونَ استخدامِ المستوى المائلِ تساوي وزنَ البرميلِ ( Fg )، كما تعلّمْتُ في الدرسِ السابقِ، ويكونُ الشغلُ اللازمُ لرفعِ البرميل رأسيًّا مسافةَ (1m): Wd = F d = 1200 × 1 = 1200 J وهذا الشغلُ يساوي الشغلَ (Wi )الذي يجبُ أن يبذلَهُ الشخصُ على البرميلِ لرفعِه على المستوى المائل، الذي طوله يساوي (3m )، عندما يكون أملس، أيْ إنَّ:
وهذا يعني أنَّ المستوى المائلَ قلّلَ القوّةَ اللازمةَ لرفعِ البرميلِ إلى الثلثِ، لكنَّه بالمقابلِ زادَ المسافةَ التي تؤثّرُ فيها القوةُ إلى ثلاثةِ أمثالِ المسافةِ الرأسيّةِ. أيْ وكأنَّ المستوى المائلَ قلّلَ القوّةَ ثلاثَ مرّاتٍ، وهذا ما يُطلقُ عليهِ اسمَ الفائدةِ الآليّةِ، وللمستوى المائلُ الأملس تعطى بالعلاقةِ:
ويُطلقُ على () بوجهٍ عامٍّ اسمَ المقاومةِ ( load )، و ( ) اسمَ القوةِ (force)، لذا تكونُ الفائدةُ الآليةُ لأيِّ آلةٍ بسيطةٍ:
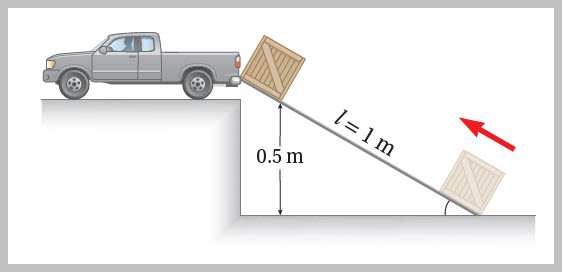
أُلاحظُ أنَّ الفائدةَ الآليّةَ تزدادُ بنقصانِ القوةِ المؤثِّرة،ِ وهذا يتحقّقُ للمستوى المائلِ بزيادةِ طولِه. مثال محلول يُرادُ رفعُ صندوقٍ وزنُه إلى سيارةِ شحنٍ عن طريقِ مستوًى مائلٍ أملسَ طولُه ، كما في الشكلِ. أحسُبُ: 1. الفائدةَ الآليّةَ للمستوى المائلِ. 2. مقدارَ القوةِ(F). الحلُّ: 2. الفائدةُ الآليّةُ = ، ،
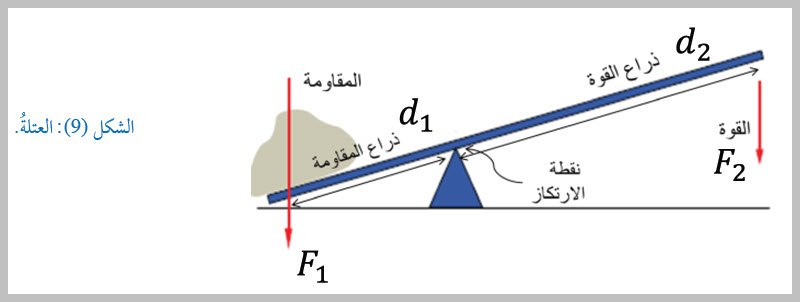
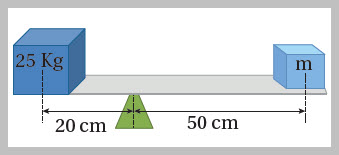
الرافعةُ Lever وهذهِ النقطةُ الثابتةُ تُسمَّى نقطةَ الارتكازِ. والشكلُ ( 9) يوضّحُ أحدَ أشكالِ الروافعِ، التي تُعرفُ بالعَتلةِ،
وتُستخدمُ في تحريكِ الأجسامِ الثقيلةِ بأقلِّ قوةٍ ممكنةٍ. وتقومُ فكرةُ عملِ الرافعةِ على التأثيرِ بقوةٍ عندَ أحدِ طرفي الساقِ، فتدورُ الساقُ حولَ نقطةِ الارتكازِ، ويرتفعُ الثِّقَلُ عندَ الطرفِ الآخرِ للساقِ، فيكونُ الشغلُ الذي تبذلُه القوةُ على أحدِ طرفي الساقِ مساويًا للشغلِ الذي يبذلُه الطرفُ الآخرُ للساقِ على المقاومةِ، على افتراضِ أنَّ الطاقةَ محفوظةُ. وعندما تكون الرافعة في حالة اتزان حول نقطة الارتكاز فإن: حيثُ: ويُطلقُ على العَلاقةِ السابقةِ اسمَ: قانونِ الرافعةِ، وتكونُ الفائدةُ الآليّةُ للرافعةِ:
أُلاحظُ أنَّهُ كلّما قلَّ طولُ ذراعِ المقاومةِ بالنسبةِ إلى طولِ ذراعِ القوةِ زادتِ الفائدةُ الآليةُ للرافعةِ، وهذا يعني أنَّنا نحتاجُ إلى قوةٍ صغيرةٍ للتغلُّبِ على مقاومةٍ كبيرةٍ. وتتعدّدُ أشكالُ الروافعِ واستخداماتُها تبعًا للمواقعِ النسبيّةِ لنقطةِ الارتكازِ، ونقطةِ تأثيرِ القوةِ، ونقطةِ تأثيرِ المقاومةِ، وهي تقعُ في ثلاثِ 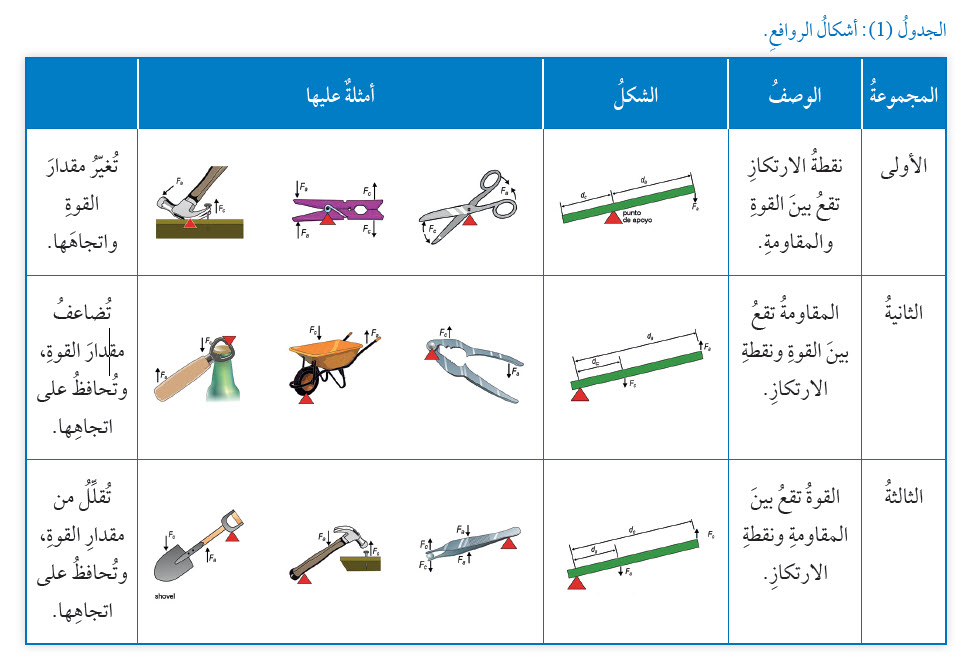
مثال محلول في الشكلِ لوحٌ خشبيٌّ استُخدِمَ كرافعة، ووضِعَ عليهِ جسمانِ فاتَّزَنا أفقيًّا على البُعْدينِ الموضَّحينِ، الحلُّ:
مثال محلول يبيّنُ الشكلُ قطّاعةَ أسلاكٍ، معتمدًا على البياناتِ المُثبَتةِ على الشكلِ، أُجيبُ عمّا يأتي: 1. أُحدّدُ إلى أيِّ مجموعةٍ تنتمي هذهِ القطّاعةُ بوصفِها تعملُ عملَ رافعةٍ. 2. أحسبُ الفائدةَ الآليّةَ لهذهِ الرافعةِ. الحلُّ:
|
|
|
تمرين في لعبةِ «السي سو » جلسَ طفلٌ وزنُه على أحدِ طرفي اللعبةِ وعلى بُعْدِ من نقطةِ الارتكازِ. أُحدّدُ على أيِّ بُعدٍ من نقطةِ الارتكازِ يجبُ أن يجلسَ طفلٌ آخرُ وزنُه على الطرفِ الآخرِ منَ اللعبةِ، بحيث يكونَ الطفلانِ في حالةِ اتزانٍ. |
|
|
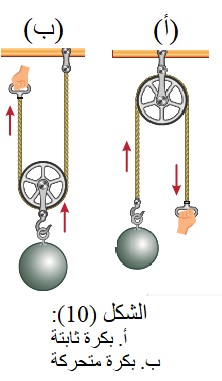
البكرةُ pulley الحبلِ المقاومةُ، وتؤثِّرُ قوّةُ الشدِّ في نهايتِه الأخرى. والبكرةُ نوعانِ، ثابتةٌ ومتحركةٌ، حيثُ تعملُ البكرةُ الثابتةُ على تغييرِ اتجاهِ القوّةٍ دونَ تغييرِ مقدارِها، كما في الشكلِ ( 10 /أ)، وتكونُ فائدتُها الآليّةُ ( 1 ) ؛ لأنَّ قوّةَ الشدِّ اللازمةِ لرفعِ الثقلِ تكونُ مساويةً لوزنِه، أيْ أنَّ القوةَ تساوي المقاومة ، في حينِ تعملُ المتحركةُ على تنصيفِ مقدارِ القوّةِ دونَ تغييرِ اتّجاهِها، كما في الشكلِ ( 10 /ب) ، وتكونُ فائدتُها الآليّةُ ( 2)؛ لأنَّ وزنَ الثقلِ يتوزّعُ على طرفي الحبلِ بالتساوي، الطرفِ المُثبتِ والطرفِ الحرِّ، لذا يكفي التأثيرُ بقوةِ شدٍّ في الطرفِ الحرِّ للحبلِ تساوي نصفَ وزنِ الثقلِ لسحبِه إلى أعلى أو خفضِه إلى أسفلَ. وتُستخدَمُ البكرةُ في رفعِ الأثقالِ أو خفضِها. ولتسهيلِ العملِ باستخدامِ البكرةِ المتحركةِ بحيثُ تصبحَ قوةُ الشدِّ إلى أسفلَ بدلً منَ الأعلى، يُوصَّلُ مع البكرةِ المتحركةِ بكرةٌ أخرى ثابتةٌ، كما في الشكلِ ( 11 /أ)، وتكونُ الفائدةُ الآليةُ للمجموعةِ ( 2)، إذْ إنَّ البكرةَ الثابتةَ لا تُغيّرُ منَ الفائدةِ الآليّةِ، إنما تُسهِّلُ العملَ فقطْ. ويُستخدمُ عادةً في رفعِ الأجسامِ الثقيلةِ نظامٌ منَ البكراتِ الثابتةِ والمتحركةِ يُثبَّتُ على روافعَ ضخمةٍ، كما في الشكلِ ( 11 /ب).
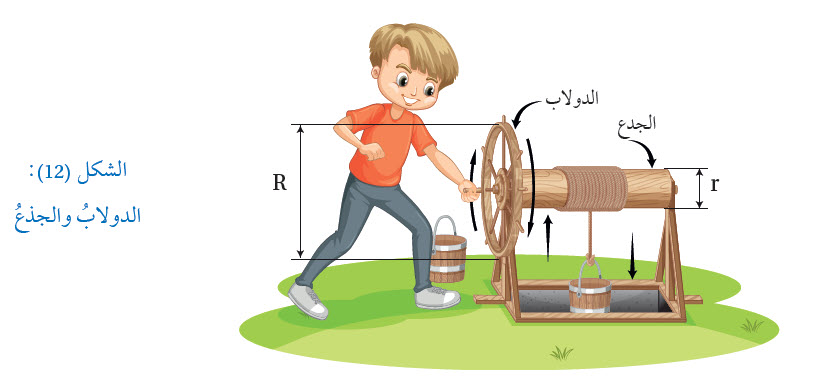
الدولابُ والجِذْعُ Wheel and Axle أصغرَ قطرًا ( r) يُسمَّى الجذعُ، كما في الشكلِ ( 12 ). أمّا فائدتُه الآليةُ فهي: النسبةُ بينَ قطرِ الدولابِ إلى قطرِ الجِذعِ. وتتعدّدُ استخداماتُ الدولابِ والجِذعِ في حياتِنا اليوميّةِ، وفي الشكلِ ( 13 ) بعْضٌ منها.
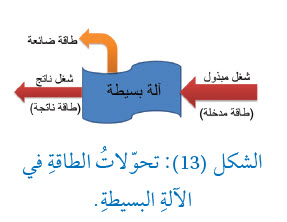
كفاءةُ الآلة Efficiency of Machine تعملُ الآلاتُ عمومًا على نقلِ الطاقةِ أو تحويلِها، فلا توجدُ آلةٌ تُنتِجُ الطاقةَ من تلقاءِ نفسِها، وقد لاحظتُ أنَّ الآلةَ البسيطةَ تعملُ عندَ التأثيرِ فيها بقوةٍ، أيْ يُبذلُ عليها شغلٌ، فتَبذلُ الآلةُ شغلً على الجسمِ، أيْ يَنتجُ عنها شغلٌ، وهو الشغلُ المفيدُ الذي نحصلُ عليهِ منَ الآلةِ. وتُقاسُ كفاءةُ الآلةِ بنسبةِ الشغلِ الناتجِ منها إلى الشغلِ المبذولِ عليها، أيْ إنَّ:
وتصلُ كفاءةُ الآلةِ إلى % 100 في الوضعِ المثاليِّ، عندَما يكونُ الشغلُ الناتجُ منَ الآلةِ مساويًا للشغلِ المبذولِ عليها، وهو ما حُسِبتْ الفائدةُ الآليةُ للآلاتِ البسيطةِ بناءً عليهِ، ولكنْ في الواقعِ العمليِّ لا توجَدُ آلةٌ بسيطةٌ أو مركّبَةٌ كفاءتُها% 100 ، وذلك بسببِ ضياعِ جزءٍ منَ الطاقةِ نتيجةَ الاحتكاكِ. والشكلُ( 14 ) يوضّحُ تحوّلاتِ الطاقةِ في الآلةِ البسيطةِ.
|
+++++ |