الأجزاءُ المتطابقةُ
تهيئة
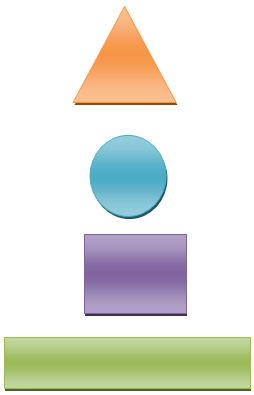
أسَمّي الأشكال الهَندسية الآتية:
أُقارِنُ إجاباتي بالإجابات الآتية:
مُثَلَّثٌ
دائِرَةٌ
مُرَبّعٌ
مُسْتَطيلٌ
تَقاسَمَ أَيْهَمُ مَعَ أُخْتِهِ قِطْعَةَ الْبَسْكَويتِ كَما في الشَّكْلِ الْآتي، هَلْ هذِهِ الْقِسْمَةُ عادِلَةٌ؟
أُجيب عن الأسئلة الآتية، حتى أتوصل إلى أنَّ القسمة عادلة أو غير عادلة:
ماذا تشاهد في الصورة؟
إلى كم جزء قُسِّمت؟
هل الجزءان متماثلان؟
هل قسمة البسكويت عادلة؟
أَتوصَّل إلى أنّ القسمة غير عادلة؛ لأنَّ الجزأين غير متماثلين، وأحدهما أكبر من الآخر.

يُمكن تقسيم الأشياء أو الأشكال إلى أجزاء متساوية، وعند توزيعها يحصل الأشخاص على قطع متماثلة تمامًا.
كما يمكن الحصول على أجزاء متساوية من خلال قصّها ووضعها فوق بعضها البعض؛ وذلك لأتأكد من أنّ الأجزاء التي تمّ تقسيمها هي أجزاء متطابقة تمامًا.
يُمْكِنُ تَقْسيمُ الكُل (whole) إِلى َ أَجزاء متطابقة (equal part)
والْأَجْزاءُ الْمُتَطابِقَةُ مِنَ الْكُلِّ لَها نَفْسُ الشَّكْلِ وَالْمَقاسِ.
مثال:
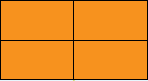
إذا أردنا تقسيم المُستطيل الآتي إلى أجزاء مُتساوية، فأيّ التقسيمين هو الصحيح؟
التقسيم الأول:
التقسيم الثاني:
لا شكَّ أنّ التقسيم الثاني هُو التقسيم الصحيح، لأنّ الأجزاء مُتساوية ومتطابقة تمامًا، فلو قمنا بوضع الأجزاء فوق بعضها لكانت متطابقة تمامًا.
أما في التقسيم الأول، فقد تمّ تقسيم المستطيل إلى أربعة أجزاء لكنها أجزاء غير متساوية وغير متطابقة، بحيث لو وضعنا الأجزاء فوق بعضها البعض لكانت غير متطابقة.
أَتَحَدَّثُ: كَيْفَ أَعْرِفُ أَنَّ الْأَجْزاءَ مُتَطابِقَةٌ في أَحَدِ الْأَشْكالِ؟
أُقارِنُ إجابتي بالإجابة الآتية:
أستطيع معرفة أنّ الأَجزاء متطابقة في أحد الأشكال من خلال قصُّ الأجزاء، ثم وضع بعضها فوق بعض.
نَشاط:
أُخصص ورقًا مُقوى لتمثيل الأشكال الآتية من خلالها، ثُمّ أَقومُ بقصّها ووضعها فوق بعضها البعض لأتأكد من أنها متطابقة أو غير متطابقة: