الأجزاءُ المُتناسِبةُ في المُثلَّثاتِ
أولًا : الأجزاءُ المُتناسِبةُ في المُثلَّث
نظرية ( التناسب في المثلث )
|
بالكلماتِ : إذا وازى مستقيمٌ ضلعًا منْ أضلاعِ مُثلَّثٍ، وقطعَ ضلعيْهِ الآخرينِ، فإنَّهُ يُقسِّمُهُما إلى قطعٍ مستقيمةٍ مُتناظِرةٍ أطوالُها مُتناسِبةٌ. بالرموزِ : إذا كانَ : ، فإنّ |
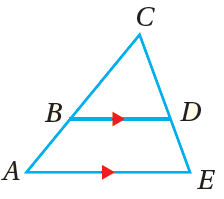 |
ثانيًا : عكسُ نظريةِ التناسبِ في المُثلَّثِ
إنَّ عكسَ نظريةِ التناسبِ في المُثلَّثِ صحيحٌ أيضًا، وهذا ما تنصُّ عليْهِ النظريةُ الآتيةُ.
نظرية (عكسُ نظريةِ التناسبِ في المُثلَّثِ)
|
بالكلماتِ : إذا قطعَ مستقيمٌ ضلعينِ في مُثلَّثٍ، وقسَّمَهُما إلى قطعٍ مستقيمةٍ مُتناظِرةٍ أطوالُها مُتناسِبةٌ، فإنَّ المستقيمَ يوازي الضلعَ الثالثَ للمُثلَّثِ. بالرموزِ : إذا كانَ ، فإنّ |
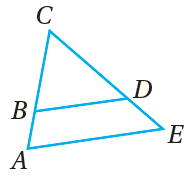 |
ثالثًا : القطعةُ المُنصِّفةُ في المُثلَّث
|
القطعةُ المُنصِّفةُ في المُثلَّثِ : هيَ قطعةٌ مستقيمةٌ طرفاها نقطتا منتصفِ ضلعين في المُثلَّثِ، وفي كلِّ مُثلَّثٍ ثلاثُ قطعٍ مُنصِّفةٍ. فمثلًا ، القطعُ المُنصِّفةُ في ΔPQR المُجاوِرِ هيَ : |
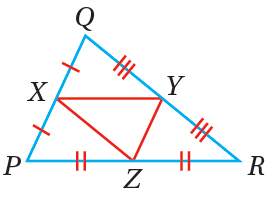 |
•• توجدُ علاقتان بينَ القطعةِ المُنصِّفة في المُثلَّث والضلعِ المُقابِل لها، وهما مُوضَّحتان في النظرية الآتية.
نظرية ( القطعة المنصفة في المثلث )
|
بالكلماتِ : القطعةُ المُنصِّفةُ في المُثلَّثِ توازي الضلعَ المُقابِلَ لها، وطولُها يساوي نصفَ طولِ ذلكَ الضلعِ. بالرموزِ : إذا كانَتِ النقطةُ D والنقطةُ E هما نقطتَيْ منتصفِ على الترتيبِ،فإنَّ :
|
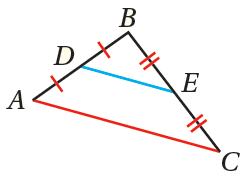 |