رياضيات فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 166

مُعتمِدًا الشكلَ المجاورَ، إذا اختيرَتْ عشوائيًّا نقطةٌ تقعُ على $\overline{RS}$ ، فأجدُ كُلًّ ممّا يأتي : a) احتمالُ وقوعِ النقطةِ على $\overline{TU}$          b) احتمالُ وقوعِ النقطةِ على $\overline{US}$   c) احتمالُ عدمِ وقوعِ النقطةِ على $\overline{US}$.

 

الحل : 

a) احتمالُ وقوعِ النقطةِ على $\overline{TU}$

أفترضُ أنَّ حادثَ وقوعِ النقطةِ على $\overline{TU}$ هوَ A. إذنْ : 

صيغةُ الاحتمالِ باستعمالِ الطولِ	$P\left(A\right) = \frac{TU}{RS}$
بتعويضِ  $TU = 6 , RS = 18$	$= \frac{6}{18} = \frac{\mathbf{1}}{\mathbf{3}}$

 

---

b) احتمالُ وقوعِ النقطةِ على $\overline{US}$

أفترضُ أنَّ حادثَ وقوعِ النقطةِ على $\overline{US}$ هوَ B. إذنْ : 

صيغةُ الاحتمالِ باستعمالِ الطولِ	$P\left(B\right) = \frac{US}{RS}$
بتعويضِ $US = 11 , RS = 18$	$= \frac{\mathbf{11}}{\mathbf{18}}$

 

---

 

c) احتمالُ عدمِ وقوعِ النقطةِ على $\overline{US}$

حادثَ عدمِ وقوعِ النقطةِ على $\overline{US}$ هوَ الحادثُ المُتمِّمُ للحادثِ B 

صيغةُ احتمالِ المُتمِّمةِ	$P\left(\overline{B}\right) = 1 - P\left(B\right)$
صيغةُ الاحتمالِ باستعمالِ الطولِ	$= 1 - \frac{US}{RS}$
بالتعويض	$= 1 - \frac{11}{18}$
بالتبسيطِ	$= \frac{\mathbf{7}}{\mathbf{18}}$

 

---

 

 

أتحقق من فهمي صفحة 167

مُعتمِدًا المعلوماتِ المعطاةَ في المثالِ 2، أجدُ احتمالَ وقوعِ السهمِ في المنطقةِ الصفراءِ.

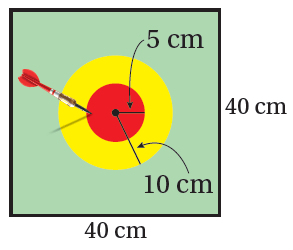
لوحةُ أسهمٍ : أطلقَ وليدٌ سهمًا على لوحةِ الأسهمِ المجاورةِ. إذا وقعَ السهمُ عشوائيًّا داخلَ اللوحةِ، فأجدُ احتمالَ وقوعِ السهمِ في المنطقةِ الحمراءِ.

الحل : 

أفترضُ أنَّ حادثَ وقوعِ السهمِ على المنطقةِ الصفراء هوَ B. إذنْ: 

صيغةُ الاحتمالِ باستعمالِ المساحةِ	$P\left(B\right) = \frac{( \mathrm{الصفراء} \mathrm{المنطقة} \mathrm{مساحة})}{(\mathrm{السهام} \mathrm{لوحة} \mathrm{مساحة})}$
مساحةِ الدائرةِ الصفراء = مساحة الدائرة الكاملة - مساحة الدائرة الحمراء	$= \frac{\mathrm{\pi }{\left(10\right)}^2-\mathrm{\pi }{\left(5\right)}^2}{{\left(40\right)}^2}$
بالتبسيط	$=\frac{75\mathrm{\pi }}{1600}$
باستعمالِ الآلةِ الحاسبةِ	$\approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{15}$

 

---

 

أتحقق من فهمي صفحة 169

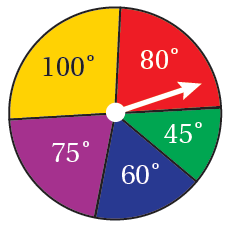
مُعتمِدًا زوايا القطاعاتِ الظاهرةَ على القرصِ المجاورِ، أجدُ كُلًّ ممّا يأتي بعدَ تدويرِ مُؤشِّرِ القرصِ: a) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأزرقِ. b) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأصفرِ أوِ القطاعِ الأحمرِ.

الحل : 

a) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأزرقِ.

أفترضُ أنَّ حادثَ توقُّفِ المُؤشِّرِ عندَ القطاعِ الأزرق هوَ A. إذنْ:

صيغةُ الاحتمالِ باستعمالِ الزوايا	$P\left(A\right) =\frac{( \mathrm{الأزرق} \mathrm{القطاع} \mathrm{زاوية})}{(\mathrm{الدائرة} \mathrm{مركز} \mathrm{حول} \mathrm{الزوايا} \mathrm{مجموع})}$
بالتعويضِ	$=\frac{60°}{360°}$
بالتبسيطِ	$=\frac{\mathbf{1}}{\mathbf{6}}$

 

b) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأصفرِ أوِ القطاعِ الأحمرِ.

أفترضُ أنَّ حادثَ توقُّفِ المُؤشِّرِ عندَ القطاعِ الأزرقِ أوِ القطاعِ الأخضر هوَ B. إذنْ : 

أتذكَّرُ : في الاحتمال ، يدلُّ حرفُ العطفِ (أوْ) على الاتحادِ.

 

صيغةُ الاحتمالِ باستعمالِ الزوايا	$P\left(B\right) =\frac{(\mathrm{والأحمر} \mathrm{الأصفر} \mathrm{القطاعين} \mathrm{زاويتي} \mathrm{مجموع} )}{(\mathrm{الدائرة} \mathrm{مركز} \mathrm{حول} \mathrm{الزوايا} \mathrm{مجموع})}$
بالتعويضِ	$=\frac{100°+80°}{360°}$
بالتبسيطِ	$=\mathbf{ }\frac{\mathbf{1}}{\mathbf{2}}$

 

---

 

 

أسئلة أتدرب وأحل المسائل

مُعتمِدًا الشكلَ المجاورَ، إذا اختيرَتْ عشوائيًّا نقطةٌ تقعُ على WZ فأجدُ كُلًّ ممّا يأتي: 1) احتمالُ وقوعِ النقطةِ على XZ   2) احتمالُ وقوعِ النقطةِ على XY 3) احتمالُ وقوعِ النقطةِ على WX أوْ YZ  4) احتمالُ وقوعِ النقطةِ على WY 5) احتمالُ عدمِ وقوعِ النقطةِ علىXY

الحل : 

1) احتمالُ وقوعِ النقطةِ على XZ 

أفترضُ أنَّ حادثَ توقُّفِ المُؤشِّرِ على XZ هوَ A. إذنْ:

$P\left(A\right) = \frac{XZ}{WZ} = \frac{8}{10} =\mathbf{ }\frac{\mathbf{4}}{\mathbf{5}}$

---

 

2) احتمالُ وقوعِ النقطةِ على XY

أفترضُ أنَّ حادثَ توقُّفِ المُؤشِّرِ على XY هوَ B. إذنْ:

$P\left(B\right) = \frac{XY}{WZ} = \frac{5}{10} =\mathbf{ }\frac{\mathbf{1}}{\mathbf{2}}$
 

---

 

3) احتمالُ وقوعِ النقطةِ على WX أوْ YZ 

أفترضُ أنَّ حادثَ توقُّفِ المُؤشِّرِ على WX أو YZ هوَ M. إذنْ:

$P\left(M\right) = \frac{WX+YZ}{WZ} = \frac{2+3}{10} =\mathbf{ }\frac{\mathbf{1}}{\mathbf{2}}$

---

4) احتمالُ وقوعِ النقطةِ على WY

أفترضُ أنَّ حادثَ توقُّفِ المُؤشِّرِ على WY هوَ N. إذنْ:

$P\left(N\right) = \frac{WY}{WZ} = \frac{\mathbf{7}}{\mathbf{10}} \mathbf{ }$

---

 

5) احتمالُ عدمِ وقوعِ النقطةِ علىXY 

احتمال عدم وقوع النقطة على XY هو الحادث المتمم للحادث B ، إذن :

$$\begin{gathered} P\left(\overline{B}\right) = 1 - P\left(B\right) \\ = 1 - \frac{1}{2} \\ = \frac{\mathbf{1}}{\mathbf{2}} \end{gathered}$$

---

  

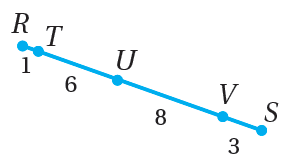
مُعتمِدًا الشكلَ المجاورَ، إذا اختيرَتْ عشوائيًّا نقطةٌ تقعُ على RS ، فأجدُ كُلًّ ممّا يأتي:

6) احتمالُ وقوعِ النقطةِ على RT

7) احتمالُ وقوعِ النقطةِ على TS

8) احتمالُ وقوعِ النقطةِ على RT أوْ US

9) احتمالُ وقوعِ النقطةِ على UR  

10) احتمالُ عدمِ وقوعِ النقطةِ على UR  

الحل : 

6) احتمالُ وقوعِ النقطةِ على RT

$\frac{5}{10} = \frac{\mathbf{1}}{\mathbf{2}}$

---

7) احتمالُ وقوعِ النقطةِ على TS

$\frac{5}{10} = \frac{\mathbf{1}}{\mathbf{2}}$

---

8) احتمالُ وقوعِ النقطةِ على RT أوْ US

$\frac{3+5}{10}=\frac{8}{10} = \frac{\mathbf{4}}{\mathbf{5}}$

---

9) احتمالُ وقوعِ النقطةِ على UR 

$\frac{5+2}{10}=\frac{\mathbf{7}}{\mathbf{10}}$

---

 

10) احتمالُ عدمِ وقوعِ النقطةِ على UR

$1 - \frac{7}{10} = \frac{\mathbf{3}}{\mathbf{10}}$

 

---

 

 

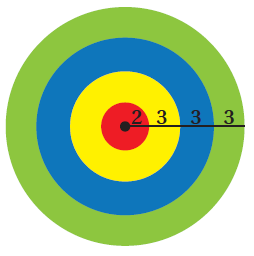
لوحةُ أسهمٍ : أطلقَتْ دلالُ سهمًا على لوحةِ الأسهمِ المجاورةِ. إذا وقعَ السهمُ عشوائيًّا داخلَ اللوحةِ، فأجدُ كُلًّ منَ الاحتمالاتِ الآتيةِ: 11) وقوعُ السهمِ على المنطقةِ الحمراءِ. 12) وقوعُ السهمِ على المنطقةِ الصفراءِ. 13) عدمُ وقوعِ السهمِ على المنطقةِ الزرقاءِ. 14) وقوعُ السهمِ على المنطقةِ الخضراءِ أوِ المنطقةِ الصفراءِ.

 

الحل : 

11) وقوعُ السهمِ على المنطقةِ الحمراءِ.

$\frac{( \mathrm{الحمراء} \mathrm{المنطقة} \mathrm{مساحة})}{(\mathrm{السهام} \mathrm{لوحة} \mathrm{مساحة})} = \frac{4\mathrm{\pi }}{121\mathrm{\pi }} = \frac{\mathbf{4}}{\mathbf{121}}$

---

 

12) وقوعُ السهمِ على المنطقةِ الصفراءِ.

$\frac{( \mathrm{الصفراء} \mathrm{المنطقة} \mathrm{مساحة})}{(\mathrm{السهام} \mathrm{لوحة} \mathrm{مساحة})} = \frac{25\mathrm{\pi }-4\mathrm{\pi }}{121\mathrm{\pi }} = \frac{21\mathrm{\pi }}{121\mathrm{\pi }} = \frac{\mathbf{21}}{\mathbf{121}}$

 

---

 

13) عدمُ وقوعِ السهمِ على المنطقةِ الزرقاءِ.

$$\begin{gathered} = 1 - \frac{64\mathrm{\pi } - 25\mathrm{\pi }}{121\mathrm{\pi }} \\ = 1 - \frac{39\mathrm{\pi }}{121\mathrm{\pi }} \\ =\mathbf{ }\frac{\mathbf{82}}{\mathbf{121}} \end{gathered}$$

---

 

14) وقوعُ السهمِ على المنطقةِ الخضراءِ أوِ المنطقةِ الصفراءِ.

$$\begin{gathered} = \frac{(121\mathrm{\pi } - 64\mathrm{\pi })+21\mathrm{\pi }}{121\mathrm{\pi }} \\ =\frac{78\mathrm{\pi }}{121\mathrm{\pi }} \\ =\mathbf{ }\frac{\mathbf{78}}{\mathbf{121}} \end{gathered}$$

 

---

 

إذا اختيرَتْ نقطةٌ عشوائيًّا منْ كلِّ شكلٍ منَ الأشكالِ الآتيةِ، فأجدُ احتمالَ وقوعِها في المنطقةِ المُظلَّلةِ باللونِ الأزرقِ:

$\frac{2\times 4 + 3\times 6}{9\times 10} = \frac{8 + 18}{90} = \frac{26}{90} = \frac{\mathbf{13}}{\mathbf{45}}$

 

$\frac{4\times 4 - 4\mathrm{\pi }}{4\times 4} = \frac{16 - 4\mathrm{\pi }}{16} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{21}$

 

$\frac{{\displaystyle \frac{1}{2}}\left(25\mathrm{\pi }\right)}{{\displaystyle \frac{1}{2}}\left(20\right)\left(10\right)} = \frac{25\mathrm{\pi }}{200}=\frac{\mathrm{\pi }}{8} \approx \mathbf{0}\mathbf{.}\mathbf{39}$

 

$\frac{36\times 18 - 2\left(81\mathrm{\pi }\right)}{36\times 18} = \frac{648 - 162\mathrm{\pi }}{648} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{21}\mathbf{ }$

 

$\frac{{\displaystyle \frac{1}{2}}(14+20)\times 12 -(14\times 12)}{\frac{1}{2}(14+20)\times 12 } = \frac{204 -168}{204} = \frac{36}{204} =\mathbf{ }\frac{\mathbf{3}}{\mathbf{17}}$

 

$\frac{10\times 16 - {\displaystyle \frac{1}{2}}\times 16\times 10}{10\times 16} = \frac{160 -80}{160} =\mathbf{ }\frac{\mathbf{1}}{\mathbf{2}}$

 

---

 

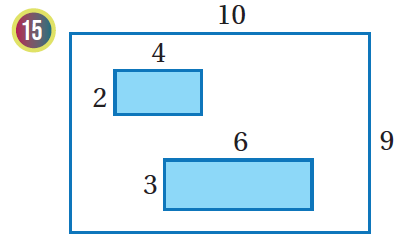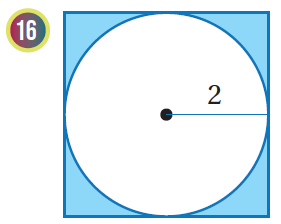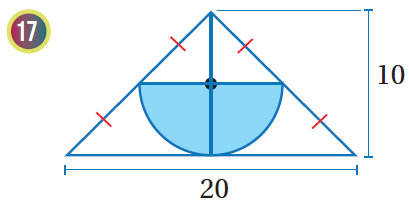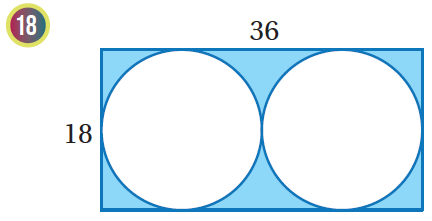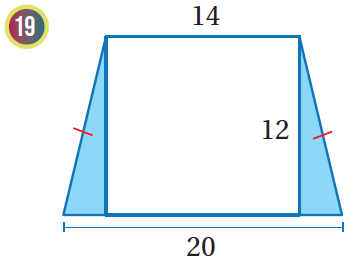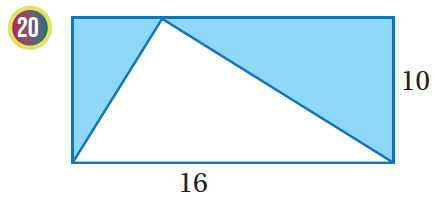مُعتمِدًا زوايا القطاعاتِ الظاهرةَ على القرصِ المجاورِ، أجدُ كُلًّ ممّا يأتي بعدَ تدويرِ مُؤشِّرِ القرصِ: 21) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ البنفسجيِّ. 22) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأصفرِ أوِ القطاعِ الأخضرِ. 23) احتمالُ عدمِ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأحمرِ.

 

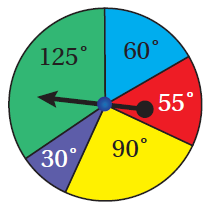الحل : 

21) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ البنفسجيِّ.

$\frac{30°}{360°} = \frac{\mathbf{1}}{\mathbf{12}}$

---

22) احتمالُ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأصفرِ أوِ القطاعِ الأخضرِ.

$\frac{90°+125°}{360°} = \frac{215°}{360°} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{6}\mathbf{ }$

---

23) احتمالُ عدمِ توقُّفِ مُؤشِّرِ القرصِ عندَ القطاعِ الأحمرِ.

$1- \frac{55°}{360°} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{85}\mathbf{ }$

---

 

مهاراتُ التفكيرِ العليا

24)  تبريرٌ : إذا كانَتِ BZ تحوي MN ، وكانَ BZ = 20 ، واختيرَتْ نقطةٌ عشوائيًّا على BZ ، وكانَ احتمالُ وقوعِها على MN هوَ 0.3 ،

فأجدُ  طولَ MN ، مُبرِّرًا إجابتي.

الحل : 

أستخدم صيغة الاحتمال باستعمال الطول

$$\begin{gathered} \frac{MN}{BZ} = 0.3 \\ \frac{MN}{20} = 0.3 \\ \mathit{M}\mathit{N}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{6} \end{gathered}$$

---

 

25) تبرير : في المستوى الإحداثيِّ المجاورِ، إذا اختيرَ الزوجُ المُرتَّبُ ( x, y ) عشوائيًّا، حيثُ : $-5 \le x \le 5$  ، و  $-5 \le y \le 5$،

فأجدُ احتمالَ ألّا يقعَ الزوجُ المُرتَّبُ في أيٍّ منَ المُثلَّثِ، والدائرةِ، ومتوازي الأضلاعِ ، مُبرِّرًا إجابتي.

الحل : 

مساحة متوازي الأضلاع  = 6 وحدة مربعة  ، مساحة الدائرة  = $4\mathrm{\pi }$ وحدة مربعة  ، مساحة المثلث = 4.5 وحدة مربعة 

مساحة المستوى الإحداثي حيثُ : $-5 \le x \le 5$ ، و  $-5 \le y \le 5$ هو  $10 \times 10 = 100$ ، إذن : 

$\frac{100 - ( 6 + 4\mathrm{\pi } + 4.5)}{100} = \frac{89.5-4\mathrm{\pi }}{100} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{77}$

---

 

26) مسألةٌ مفتوحة : مُعتمِدًا AE ، أَصِفُ حادثًا احتمالُهُ أكبرُ منْ 2/1 (أكتبُ ثلاثةَ حلولٍ مُمكِنةٍ). 

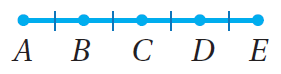
الحل : 

1) وقوع النقطة على AD 

2) وقوع النقطة على BE

3) وقوع النقطة على AC أو DE              

 

---

 

 

أسئلة كتاب التمارين

مُعتمِدًا الشكلَ المجاورَ، إذا اختيرَتْ عشوائيًّا نقطةٌ تقعُ على AF ، فأجدُ كُلًّ ممّا يأتي: 1) احتمالُ وقوعِ النقطةِ على CD 2) احتمالُ وقوعِ النقطةِ على BE 3) احتمالُ وقوعِ النقطةِ على EF أوْ AB 4) احتمالُ عدمِ وقوعِ النقطةِ على DE

الحل : 

1) احتمالُ وقوعِ النقطةِ على CD

$\frac{CD}{AF} = \frac{6}{18} = \frac{\mathbf{1}}{\mathbf{3}}$

---

2) احتمالُ وقوعِ النقطةِ على BE

$\frac{BE}{AF} = \frac{\mathbf{11}}{\mathbf{18}}$

---

3) احتمالُ وقوعِ النقطةِ على EF أوْ AB

$\frac{BE}{AF} = \frac{2+5}{18} =\frac{\mathbf{7}}{\mathbf{18}}$

---

4) احتمالُ عدمِ وقوعِ النقطةِ على DE

$1-\frac{DE}{AF} = 1 - \frac{2}{18} = \frac{\mathbf{8}}{\mathbf{9}}$

 

---

 

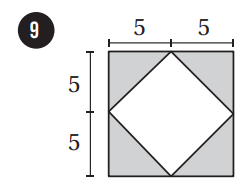
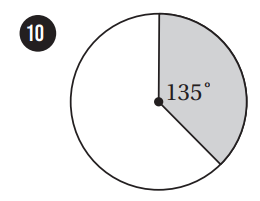
إذا اختيرَتْ نقطةٌ عشوائيًّا منْ كلِّ شكلٍ منَ الأشكالِ الآتيةِ، فأجدُ احتمالَ وقوعِها في المنطقةِ المُظلَّلةِ باللونِ الأزرقِ:

$\frac{{\displaystyle \frac{1}{2}}(7+16)\times 4 - (7\times 4)}{\frac{1}{2}(7+16)\times 4} = \frac{46 - 28}{46} =\frac{18}{46} = \frac{\mathbf{9}}{\mathbf{23}}$
$\frac{80\times 80 - 2({\displaystyle \frac{1}{2}}\times 80\times 40)}{80\times 80} = \frac{6400 -3200}{6400} =\frac{3200}{6400} = \frac{\mathbf{1}}{\mathbf{2}}$
$\frac{{\displaystyle \frac{1}{2}}(6\times 7)}{{\displaystyle \frac{1}{2}}(12\times 14)} = \frac{21}{84} = \frac{\mathbf{1}}{\mathbf{4}}$
$\frac{4\mathrm{\pi } - {(2\sqrt{2} )}^2}{4\mathrm{\pi }} = \frac{4\mathrm{\pi }-8}{4\mathrm{\pi }} = \frac{4(\mathrm{\pi }-2)}{4\mathrm{\pi }} = \frac{\mathrm{\pi }-2}{\mathrm{\pi }} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{36}$
$\frac{10\times 10 - {\left(\sqrt{50}\right)}^2}{100} = \frac{100 - 50 }{100} =\mathbf{ }\frac{\mathbf{1}}{\mathbf{2}}$
$\frac{135°}{360°} = \frac{\mathbf{3}}{\mathbf{8}}$

 

---

 

 

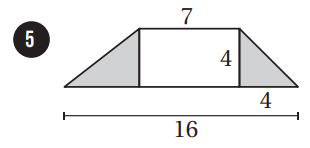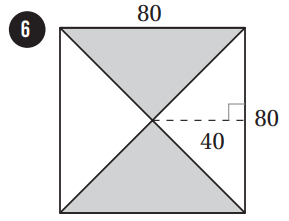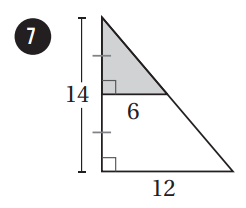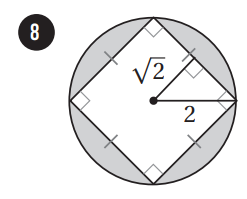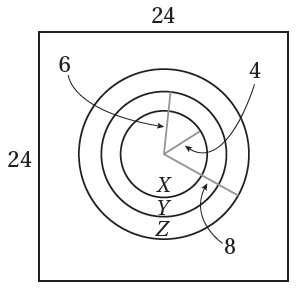
إذا وقعَ سهمٌ رُمِيَ عشوائيًّا داخلَ لوحةِ الأسهمِ المجاورةِ، فأجدُ كُلًّ منَ الاحتمالاتِ الآتيةِ : 11) وقوعُ السهمِ في المنطقةِ X 12) وقوعُ السهمِ في المنطقةِ Y 13) عدمُ وقوعِ السهمِ في المنطقةِ Z 14) عدمُ وقوعِ السهمِ في المنطقةِ X

 

الحل : 

11) وقوعُ السهمِ في المنطقةِ X

$\frac{16\mathrm{\pi }}{24\times 24} =\frac{16\mathrm{\pi }}{576} \approx \mathbf{0}\mathbf{.}\mathbf{09}\mathbf{ }$

---

12) وقوعُ السهمِ في المنطقةِ Y

$\frac{36\mathrm{\pi } - 16\mathrm{\pi }}{24\times 24} = \frac{20\mathrm{\pi }}{576} \approx \mathbf{0}\mathbf{.}\mathbf{11}$

---

13) عدمُ وقوعِ السهمِ في المنطقةِ Z

$1 - \frac{64\mathrm{\pi } - 36\mathrm{\pi }}{24\times 24} = 1 - \frac{28\mathrm{\pi }}{576} \approx \mathbf{ }\mathbf{0}\mathbf{.}\mathbf{85}$

---

14) عدمُ وقوعِ السهمِ في المنطقةِ X

$1-\frac{16\mathrm{\pi }}{24\times 24} = 1 - \frac{16\mathrm{\pi }}{576} = \mathbf{0}\mathbf{.}\mathbf{91}$

---