رياضيات11 فصل أول

الاقترانات الأسية

الاقتران الأسي: هو اقتران على الصورة$f\left(x\right)=a{b}^x$ حيث a و b عددان حقيقيان و $a\ne 0 , b\ne 0 , b>0$

ملاحظة: لتمثيل الاقتران الأسي بيانيا

1) نقوم بإنشاء جدول قيم

2) نعين الأزواج المرتبة الناتجة من الجدول في المستوى الإحداثي .

3) نقوم بالتوصيل بين النقاط الممثلة بمنحنى متصل.

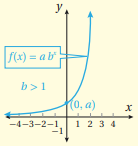
أولا: تمثيل الاقتران الأسي على الصورة $f\left(x\right)=a{b}^x$ حيث $a>0 , b>1$ وتعرف خصائصه

 

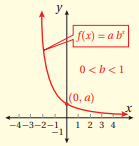
ثانيا: المثيل البياني للاقتران الأسي على الصورة $f\left(x\right)=a{b}^x$ حيث $0<b<1 , a>0$  وتعرف خصائصه

 

خصائص الاقتران الأسي

التمثيل البياني للاقتران الأسي المعرف على الصورة $f\left(x\right)=a{b}^x$ حيث b, a عددان حقيقيان و $a\ne 0 , b\ne 1 , b>0$ له الخصائص الآتية: مجال الاقتران هو مجموعة الأعداد الحقيقية R. مدى الاقتران هو مجموعة الأعداد الحقيقية الموجبة $R^{+}$ أي الفترة $(0,\infty )$. يكون الاقتران متزايدًا إذا كانت b>1 يكون الاقتران متناقصًا إذا كانت $0<b<1$ للاقتران خط تقارب أفقي هو المحور x. يقطع الاقتران المحور y في نقطة واحدة هي $(0,a)$، ولا يقطع المحور x. اقتران واحد لواحد.

 

النمو والاضمحلال

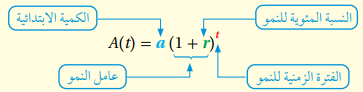
اقتران النمو الأسي: إذا ازدادت كمية بنسبة مئوية ثابتة خلال فترات زمنية متساوية فإنها تزداد بشكل أسي ولإيجاد مقدار هذه الكمية التي زدادت بعد t من الزمن يمكن استعمال الاقتران الآتي: $A\left(t\right)=a{(1+r)}^t$ حيث:

A(t) هو اقتران النمو الأسي، t الفترة الزمنية ، a الكمية الابتدائية ، r النسبة المئوية لنمو في فترات زمنية محددة ويسمى أساس العبارة الأسية (1+r) عامل النمو.

اقتران النمو الأسي هو كل اقتران أسي يتزايد بنسبة مئوية  ثابتة في فترات زمنية  متساوية.

 

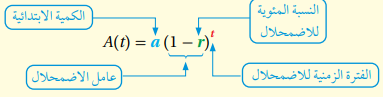
اقتران الاضمحلال الأسي: إذا نقصت كمية بنسبة مئوية ثابتة خلال فترات زمنية متساوية فإنها تنقص بشكل أسي ولإيجاد مقدار هذه الكمية التي نقصت بعد t من الزمن يمكن استعمال الاقتران الآتي:$A\left(t\right)=a{(1-r)}^t$ حيث:

A(t) هو اقتران الاضمحلال الأسي، t الفترة الزمنية ، a الكمية الابتدائية ، r النسبة المئوية للاضمحلال في فترات زمنية محددة ويسمى أساس العبارة الأسية ($1-r$) عامل الاضمحلال.

اقتران الاضمحلال الأسي اقتران أسي يتناقص بنسبة مئوية ثابتة في فترات زمنية متساوية.

 

الاقتران الأسي الطبيعي: عندما يكون الأساس في الاقتران الأسي هو العدد النيبيري الغير النسبي $e=2.718281828....$ فإن الاقتران $f\left(x\right)=e^x$ يسمى الاقتران الأسي الطبيعي وله الخصائص نفسها للاقتران $f\left(x\right)=a^x$