رياضيات12 فصل أول

ملخص الدرس الثالث: الاقترانات اللوغاريتمية:

 

الاقتران اللوغاريتمي للأساس b هو الاقتران العكسي للاقتران الأسي: $f\left(x\right)=b^x$ ، حيث أن:$b>0, b\ne 1$

ويرمز إليه بالرمز:$g\left(x\right)= {\log }_b x$ 

                 ويُقرأ: لوغاريتم $x$ للأساس $b$

 

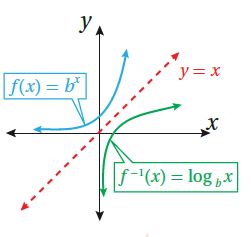
ويبين الشكل التمثيل البياني للاقترانين:

 

 

 

 

 

 

العلاقة بين الصورة الأسية والصورة اللوغاريتمية:

 

 

 

 

 

 

 

 

 

 

 

* يمكن استعمال تعريف اللوغاريتم في تطبيقات رياضية عدة:

أولًا: لتحويل المعادلة من الصورة اللوغاريتمية إلى الصورة الأسية : (مثال: ${\log }_2 128 = 7 \to 2^7 = 128$)

ثانيًا: لتحويل المعادلة من الصورة الأسية إلى الصورة اللوغاريتمية: (مثال: $3^4=81 \to {\log }_3 81=4$)

ثالثا: إيجاد قيمة العبارة اللوغاريتمية باستعمال قوانين الأسس:(مثال:جد قيمة ${\log }_2 8$ دون استخدام الآلة الحاسبة)

                                                                                                                                                   الحل:  ${\log }_{2}8 = y \to 2^y=8 2^y =2^3 \therefore y =3$

 

* الخصائص الأساسية للوغاريتمات:

 

 

 

 

 

 

 

 

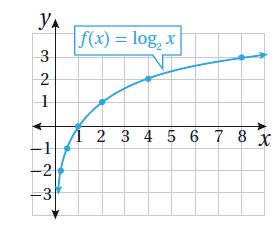
* تمثيل الاقتران اللوغاريتمي بيانيًا:

استعمل العلاقة العكسية بين الاقتران الأسي واللوغاريتمي لتمثيل الاقتران اللوغاريتمي

 

 

 

 

 

 

 

* خصائص الاقتران اللوغاريتمي:

 

 

 

 

 

 

 

 

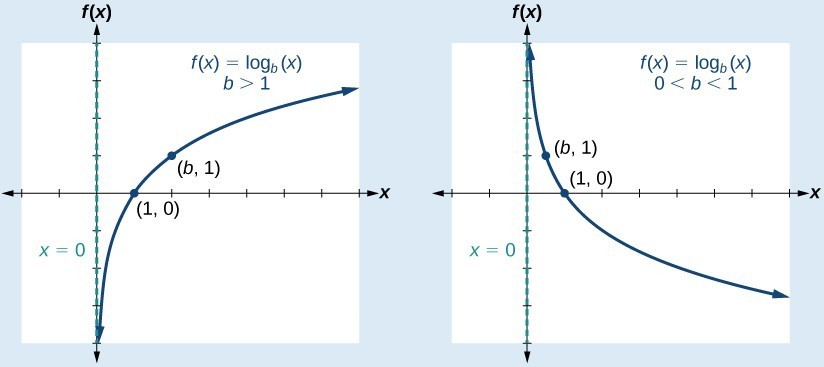
مجال الاقتران : هو مجموعة الأعداد الحقيقية الموجبة $\left(0, \infty \right)$

مدى الاقتران : هو مجموعة الأعداد الحقيقية $\mathrm{ℝ}$

الاقتران متزايد : إذا كان $b>1$

الاقتران متناقص: إذا كان $0 <b <1$

خط التقارب : يوجد خط تقارب رأسي للاقتران هو المحور $y$

المقاطع: الاقتران يقطع المحور x  في نقطة واحدة هي(0, 1) ، ولا يقطع المحور $y$

 

* مجال الاقتران اللوغاريتمي في صورة :$f\left(x\right)=lo{g}_{b}g\left(x\right)$

هو جميع قيم $x$  في مجال $g\left(x\right)$، التي يكون عندها$g\left(x\right)>0$

(مثال: مجال الاقتران ${\log }_4(x-1)$ هو $(1,\infty )$