الاقترانات اللوغاريتمية
الاقتران اللوغاريتمي: هو الاقتران العكسي للاقتران الأسي ويسمى الاقتران اللوغاريتمي للأساس b ويرمز له بالرمز ويقرأ لوغاريتم x للأساس b.
أي أن إذا كان حيث فإن .
العلاقة بين الصورتين الأسية واللوغاريتمية
|
إذا كان x >0 و فإن:
|
التحويل من الصورة اللوغاريتمية إلى الصورة الأسية:
مثال:
اكتب كل معادلة لوغاريتمية مما يأتي على الصورة الأسية:
التحويل من الصورة الأسية إلى الصورة اللوغاريتمية:
مثال:
أكتب كل معادلة أسية مما يأتي على الصورة اللوغاريتمية:
ملاحظة: اللوغاريتم هو أس حيث يمكنني إيجاد قيمة عبارات لوغاريتمية بسيطة باستعمال قوانين الأسس.
مثال:
أجد قيمة كل مما يأتي دون استعمال الآلة الحاسبة:
الخصائص الأساسية للوغارتمات
|
إذا كان x >0 و فإن |
مثال:
أجد قيمة كل مما يأتي دون استعمال الآلة الحاسبة:
اللوغاريتم الاعتيادي واللوغاريتم الطبيعي
1) إذا كان أساس اللوغارتم هو 10 فنسمي اللوغاريتم باللوغاريتم الاعتيادي أو وعادة يكتب بدون أساس حيث أن اللوغاريتم الاعتيادي هو الاقتران العكسي للاقتران الأسي ، أي أن ، إذا وفقط إذا .
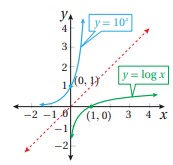
2) إذا كان أساس اللوغاريتم هو العدد النيبيري e فنسمي اللوغاريتم باللوغاريتم الطبيعي أو ln x حيث أن اللوغاريتم الطبيعي y=ln x هو الاقتران العكسي للاقتران الأسي الطبيعي أي أن y=ln x إذا وفقط إذا
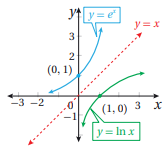
ملاحظة:
1) خصائص اللوغاريتمات صحيحة للوغاريتم الاعتيادي واللوغاريتم الطبيعي
2) يمكننا إيجاد قيمة اللوغاريتم الاعتيادي باستخدام الآلة الحاسبة بالضغط على زر log ويمكننا إيجاد قيمة اللوغاريتم الطبيعي باستخدام الآلة الحاسبة بالضغط على زر ln.
مثال:
أستعمل الآلة الحاسبة لإيجاد قيمة كل مما يأتي مقربا إجابتي إلى أقرب جزء من عشرة:
تمثيل الاقتران اللوغاريتمي بيانيا
لتمثيل الاقتران اللوغاريتمي بيانيا يمكننا استعمال العلاقة العكسية بين الاقتران اللوغارتمي والاقتران الأسي.
مثال:
أمثل كل من الاقترانات الآتية بيانيا ثم أحدد مجاله ومداه ومقطعيه الإحداثيين وخطوط تقاربه وإن كان متزايدا أم متناقصا:
نعلم أن المعادلة تكافئ المعادلة لذلك نختار قيم y ثم نجد قيم x كما في الجدول الآتي
| 16 | 4 | 1 | |||
| 2 | 1 | 0 | 1- | 2- | y |
| (x,y) |
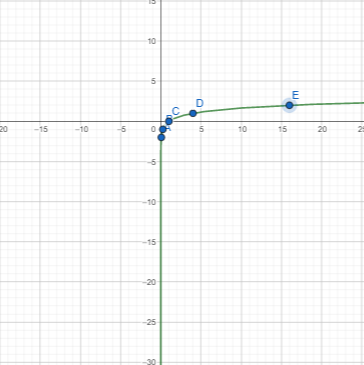
1) مجال الاقتران هو
2) مدى الاقتران هو مجموعة الأعداد
3) المقطع x هو 1، ولا يوجد مقطع للاقتران مع المحور y لأن X>0 دائما
4) يوجد للاقتران خط تقارب رأسي وهو المحور y
5) الاقتران متزايد
نعلم أن المعادلة تكافئ المعادلة ذلك نختار قيم y ثم نجد قيم x كما في الجدول الآتي
| 1 | 4 | 16 | |||
| 2 | 1 | 0 | 1- | 2- | y |
| (x,y) |
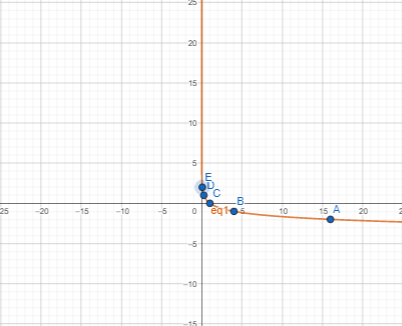
1) مجال الاقتران هو
2) مدى الاقتران هو مجموعة الأعداد
3) المقطع x هو 1، ولا يوجد مقطع للاقتران مع المحور y لأن X>0 دائما
4) يوجد للاقتران خط تقارب رأسي وهو المحور y
5) الاقتران متناقص
من خلال التمثيل البياني لبعض الاقترانات نتوصل إلى بعض خصائص الاقتران اللوغاريتمي:
خصائص الاقتران اللوغاريتمي
|
التمثيل البياني للاقتران اللوغاريتمي على الصورة حيث b عدد حقيقي و له الخصائص الآتية: 1) مجال الاقتران هو مجموعة الأعداد الحقيقية الموجبة أي الفترة . 2) مدى الاقتران هو مجموعة الأعداد الحقيقية R. 3) يكون الاقتران متزايدا إذا كانت b>1 4) يكون الاقتران متناقصا إذا كانت 5) للاقتران خط تقارب رأسي هو المحور y. يقطع الاقتران المحور x في نقطة واحدة هي (1,0)، ولا يقطع المحور y. |
مثال:
علوم: يعرف الرمز pH باسم الرقم الهيدروجيني، وهو القياس الذي يحدد إذا كان السائل قاعديا أم حمضيا أم متعادلا، ويمكن إيجاد الرقم الهيدروجيني (pH) للسوائل عن طريق المعادلة حيث تمثل تركيز أيونات الهيدروجين في المول لكل لتر (mol/L).
1) أجد الرقم الهيدروجيني (pH) لسائل تنظيف منزلي تركيز أيونات الهيدروجين فيه ، ثم أحدد إذا كان السائل حمضيا أم قاعديا.
إذن: الرقم الهيدروجيني (pH) لسائل التنظيف 11، ما يعني أنه قاعدي.
2) أجد الرقم الهيدروجيني (pH) لعينة مطر تركيز أيونات الهيدروجين فيها ثم أحدد إذا كان الرقم الهيدروجيني للعينة أقل أم أكبر من الرقم الهيدروجيني للأمطار الطبيعية والذي يساوي 5.6 ( أقرب إجابتي إلى أقرب جزء من عشرة).
إذن: الرقم الهيدروجيني (pH) لعينة المطر 3.7 تقريبا، وهو أقل من الرقم الهيدروجيني للأمطار الطبيعية.
