الاقترانُ التربيعيُّ

Quadratic Function

فكرةُ الدرسِ : 

• تعرُّفُ الاقترانِ التربيعيِّ وخصائصِهِ.

• تمثيلُ الاقترانِ التربيعيِّ بيانيًّا في المُستوى الإحداثيِّ.

أولًا : خصائصُ الاقترانِ التربيعيِّ

الاقترانُ التربيعيُّ : اقترانٌ يمكنُ كتابتُهُ عَلى الصورةِ   $f\left(x\right) = a{x}^2+ bx + c$ ؛ حيثُ a و b و c أعدادٌ حقيقيَّةٌ، وَ a ≠ 0 ، والتي تُسَمّى الصورةَ

القياسيَّةَ للاقترانِ التربيعيِّ ، وَمِنْ أمثلتِهِ : 

 $f\left(x\right) 5x^2 -2x + 1 h\left(x\right) = x^{2 }+ 4x g\left(x\right) = 8x^2$

 

•• يُعَدُّ الاقترانُ  $f\left(x\right) = x^2$ أبسطَ صورِ الاقترانِ التربيعيِّ ؛ لِذا يُسَمّى الاقترانَ الرئيسَ لعائلةِ الاقتراناتِ التربيعيَّةِ.

 

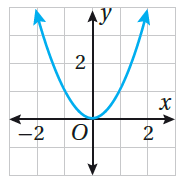يأخذُ التمثيلُ البيانيُّ للاقترانِ التربيعيِّ شكلَ الحرفِ الإنجليزيِّ U ، وَيُسَمّى قطعًا مُكافِئًا ، كما في الشكلِ المُجاورِ ، الذي يُظهِرُ التمثيلَ البيانيَّ  للاقترانِ $f\left(x\right) = x^2$

 

 

 

 

 

 

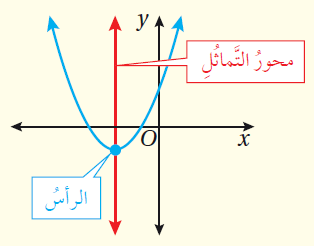
محورُ التَّماثُلِ :  هُوَ المُستقيمُ الرأسيُّ الذي يقسِمُ القطعَ المُكافِئَ إلى جُزأيْنِ مُتطابقَيْنِ، ويقطعُهُ في نقطةٍ واحدةٍ تُسَمّى الرأسَ 

مفهومٌ أساسيٌّ (محورُ تَماثُلِ الاقترانِ التربيعيِّ ورأسُهُ) 

مُعادلةُ محورِ التَّماثُلِ لمُنحنى الاقترانِ التربيعيِّ  $f\left(x\right) = a{x}^2+ bx + c$ ؛ حيثُ a ≠ 0 هي :  $x = - \frac{b}{2a}$  وإحداثِيّا رأسِهِ هما :  $\left(-\frac{b}{2a} , f(-\frac{b}{2a})\right)$

 

 

 

 

 

 

 

مثال  : 

أَجدُ مُعادلة محور التماثل ، وإحداثيّي رأس الاقتران التربيعيّ $f\left(x\right) = 2x^2 +8x-1$

الحل : 

  a = 2 و  b = 8 ، فيمكنُ إيجادُ مُعادلةِ محورِ التَّماثُلِ كالآتي:

مُعادلةُ محورِ التَّماثُلِ	$x = - \frac{b}{2a}$
بتعويض a = 2 , b = 8	$x = - \frac{8}{2\times 2 }$
بالتبسيطِ	$x = -2$

 

 

 

 

إذن ، مُعادلةُ محور التماثل هي :  x = - 2 

لإيجادِ إحداثِيَّيِ الرأسِ، أعتبرُ القيمةَ الناتجةَ عَنْ مُعادلةِ محورِ التَّماثُلِ هِيَ الإحداثيُّ x لرأسِ القطعِ المُكافِئِ، ثمَّ أُعَوِّضُها في قاعدةِ الاقترانِ لإيجادِ

الإحداثيِّ y .

الاقترانُ المُعطى	$f\left(x\right) = 2x^2 +8x-1$
بتعويضِ x = - 2	$f\left(x\right) = 2{(-2)}^2 +8(-2)-1$
بالتبسيطِ	$f\left(x\right) =\mathbf{-}\mathbf{9}$

 

 

 

إذنْ، إحداثِيّا الرأسِ $(-2 , -9)$

---

••• مجال الاقتران التربيعي ومداه 

يكونُ التمثيلُ البيانيُّ للاقترانِ التربيعيِّ $f\left(x\right) = a{x}^2+ bx + c$  ؛ حيثُ a ≠ 0 ، مفتوحًا للأعلى إذا كان a > 0 ، وَتُسَمّى أدنى نقطة فيه نقطة القيمة

الصُّغرى ، ويكون مفتوحًا للأسفل إذا كان a < 0 ، وتُسمى أعلى نقطة فيه نقطة القيمة العُظمى ، وتُمثل نقطة القيمة الصُّغرى أو نقطة القيمة

العُظمى رأس القطع  المُكافئ.

 

 

مجال الاقتران التربيعيِّ هُو جميع الأعداد الحقيقية ، أمّا مَداهُ فيمكن تحديدُهُ كالآتي :

مفهوم أساسيّ (مَدى الاقتران التربيعيّ) 

إذا كان $f\left(x\right) = a{x}^2+ bx + c$  ؛ حيثُ a ≠ 0 ، فإنَّ مَدى (f(x يكونُ :

• مجموعة الأعداد الحقيقية التي تزيد على القيمة الصُّغرى أو تُساويها إذا كان a > 0  

• مجموعة الأعداد الحقيقية التي تقلّ عن القيمة العُظمى أو تُساويها إذا كان a < 0

 

مثال  : 

لِكُلِّ قطعٍ مُكافِئٍ ممّا يأتي، أَجِدُ القيمةَ العُظمى أوِ الصُّغرى والمجالَ والمَدى واتِّجاهَ الفتحةِ :

$1) f(x) = x^2 -2x + 4 2) h\left(x\right) = -x^2+4x +8$

الحل :

$1) f(x) = x^2 -2x + 4$ 

في الاقتران f(x) : $a = 1 , b = -2$

بما أنَّ a > 0 فالتمثيلُ البيانيُّ للاقترانِ التربيعيِّ يكونُ مفتوحًا للأعلى، ويكونُ للاقترانِ قيمةٌ صُغرى يمكنُ إيجادُها كالآتي:

الخطوةُ 1 : أَجِدُ الإحداثِيَّ x للرأسِ.

الإحداثيُّ x للرأسِ	$x = - \frac{b}{2a}$
بتعويض $a = 1 , b = -2$	$x = - \frac{-2}{2\times 1}$
بالتبسيط	$x = 1$

 

 

 

 

 

الخطوةُ 2 : أَجِدُ الإحداثِيَّ y للرأسِ.

الاقترانُ المُعطى	$f\left(x\right) = x^2 -2x + 4$
بتعويضِ x = 1	$f\left(1\right) = {\left(1\right)}^2 -2\left(1\right) + 4$
بالتبسيطِ	$= 3$

 

 

 

 

إذنْ، القيمةُ الصُّغرى للاقترانِ هِيَ 3

المجالُ : جميعُ الأعدادِ الحقيقيَّةِ أوِ الفترةِ $(-\infty , \infty )$  

المَدى : { y | y ≥ 3 } أوِ الفترةِ  $[ 3 , \infty )$

---

$2) h(x) = -x^2+4x +8$

في الاقتران h(x) : $a = -1 , b = 4$

بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للاقترانِ التربيعيِّ يكونُ مفتوحًا للأسفلِ، ويكونُ للاقترانِ قيمةٌ عُظمى يمكنُ إيجادُها كالآتي :

الخطوةُ 1 : أَجِدُ الإحداثِيَّ x للرأسِ.

الإحداثيُّ x للرأسِ	$x = - \frac{b}{2a}$
بتعويض $a = -1 , b = 4$	$x = - \frac{4}{2\times -1}$
بالتبسيطِ	$x = 2$

 

 

 

 

 

الخطوةُ 2 : أَجِدُ الإحداثِيَّ y للرأسِ.

الاقترانُ المُعطى	$h\left(x\right) =-x^2+4x+8$
بتعويضِ x = 3	$h\left(2\right) =-{\left(2\right)}^2+4\left(2\right)+8$
بالتبسيطِ	$=12$

 

 

 

إذن، القيمة العظمى للاقتران هي 12

المجال : جميع الأعداد الحقيقية أو الفترة $(-\infty , \infty )$

المدى :$\{ y | y\le 12 \}$ أوِ الفترةِ $(-\infty , 12 ]$

---

تطبيقات حياتية على الاقترانات التربيعية 

مثال : 

يُمَثِّلُ الاقترانُ  $h\left(t\right) = -12t^2+ 48t$ ارتفاعَ كرةِ قدمٍ عنْ سطحِ الأرضِ بالأقدامِ ، بعدَ t ثانيةً مِنْ ركلِها.

a) أَجِدُ ارتفاعَ الكرةِ بعدَ 3 ثوانٍ مِنْ ركلِها.

b) أَجِدُ أقصى ارتفاعٍ تصلُ إليهِ الكرةُ.

الحل :

a) أَجِدُ ارتفاع الكرة بعد ثانية من ركلِها.

الاقتران المُعطى يُمثل الارتفاع ، t تمثل الزمن ، إذن أعوض في الاقتران المعطى t = 1 لأجد الارتفاع بعد 1 ثانية

$$\begin{gathered} h\left(1\right) = -12{\left(1\right)}^2+ 48\left(1\right) \\ h\left(1\right) = -12+48 \\ h\left(1\right) = 36 \end{gathered}$$

إذن ، ارتفاع الكرة بعد ثانية واحدة من ركلها يساوي 36 قدم . 

---

b) أَجِدُ أقصى ارتفاعٍ تصلُ إليهِ الكرة.

تصل الكرة إلى أقصى ارتفاعٍ لها عندَ رأس القطع المكافئ؛ لذا أَجدُ القيمة العُظمى للقطع.

الخطوة 1 : أَجِدُ الإحداثِيَّ x للرأسِ.

الإحداثيُّ x للرأسِ	$x = - \frac{b}{2a}$
بتعويضِ  $a = -12 , b =48$	$x = - \frac{48}{2\times -12}$
بالتبسيطِ	$x = 2$

 

 

 

 

 

الخطوة 2 : أَجدُ الإحداثيّ y للرأس.

الاقترانُ المُعطى	$h\left(t\right) = -12t^2+48t$
بتعويضِ t = 2	$h\left(2\right) = -12{\left(2\right)}^2+ 48\left(2\right)$
بالتبسيطِ	$= 48$

 

 

 

إذنْ، أقصى ارتفاعٍ تصلُ إليهِ الكره هو 48 قدم .

---

ثانيًا : تحديد خصائص الاقتران التربيعيّ من تمثيله البيانيّ

يُمكنني تحديد خصائص الاقتران التربيعي من تمثيله البياني ، والمثال التالي يوضح ذلك .

مثال : 

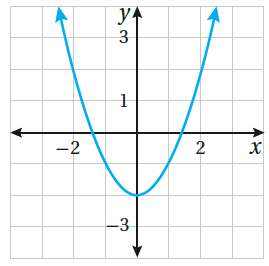أَجدُ رأس ومُعادلة محور التماثل، والقيمة العُظمى أو الصُّغرى ومَجال ومَدى القطع المُكافئ المُمَثل بيانِيًّا في المُستوى الإحداثِيِّ المُجاور:

 

 

 

 

 

 

 

الحل :

الخطوةُ 1 : أَجدُ إحداثيَّي الرأس.

بما أنَّ القطع مفتوحٌ للأعلى فالرأس يُمثل نقطتَهُ الصغرى، وهي ( 3- , 0).
 

الخطوةُ 2 : أَجِدُ مُعادلة محور التماثل.

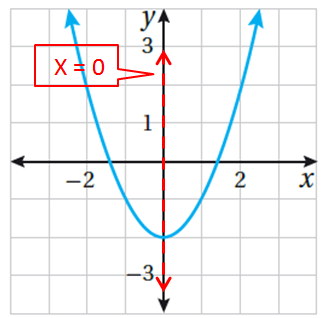بما أنَّ محور التماثل هُو المُستقيم الذي يقسِمُ القطع المُكافئ إلى جزأيْن متطابقَيْنِ ، ويقطع القطع المُكافئَ في الرأس، فإنَّ مُعادلة محور التماثل هي x = 0

 

 

 

 

 

 

الخطوةُ 3 : أَجدُ القيمة الصغرى.

بما أنَّ القيمة الصغرى هي الإحداثيُّ y لنقطة الرأس، فإنَّ القيمة الصغرى للاقتران هي 2-.
 

الخطوةُ 4 : أَجِدُ المجال والمَدى.

المجالُ: جميعُ الأعدادِ الحقيقيَّةِ أوِ الفترةِ $(-\infty , \infty )$ 

المَدى : $\{ y | y \ge -2 \}$   أوِ الفترةِ $[ -2 , \infty )$ .

---

 

ثالثًا : تمثيلُ الاقترانِ التربيعيِّ بيانيًّا

يمكنُ استعمالُ خصائصِ الاقترانِ التربيعيِّ لتمثيلِهِ بيانيًّا.

مفهومٌ أساسيٌّ (تمثيلُ الاقترانِ التربيعيِّ بيانيًّا)

لتمثيل الاقتران التربيعيِّ بيانيًّا، أتَّبِع الخُطوات الآتية: الخطوة 1 : أُحَدِّدُ اتِّجاه فتحة القطع المُكافئِ، وأَجدُ مُعادلة محور التماثل وإحداثيَّي الرأس، وأُحدِّدُ إذا كان يُمثل نقطة                    صُغرى أمْ نقطة عُظمى. الخطوة 2 : أَجِدُ نقطة تقاطع الاقتران مع المحور y. الخطوة 3 : أَجِدُ نقطة أُخرى باختيار قيمة لِـ x تقع في الجانب الذي يقعُ فيه المقطع y يمين محور التماثل أو يسارَه. الخطوة 4 : أُمثلُ رأس القطع والنقطتين اللتَيْن أوجدتُهُما من الخُطوتَيْن 2 و 3، ثمَّ أستعمل التماثُل لأعكس                               النقطتَيْن من الخُطوتين 2 و 3 حولَ محور التماثل؛ لإيجادِ نقطتين أُخرَيَيْن على التَّمثيل البيانيِّ. الخطوة 5 : أصلُ بين النقاط بمُنحنًى أملس.

 

 

 

 

 

 

 

 

 

مثال : 

أُمثل الاقتران : $f\left(x\right) = x^2+4x+1$ بيانيًّا.

الحل :

الخطوة 1 : أُحَدِّدُ اتِّجاهَ فتحة القطع المُكافئ، وأَجِدُ مُعادلة محور التماثل وإحداثِيَّي الرأس ، وأُحَدِّد إذا كان يُمثل نقطة صُغرى أم نقطة عُظمى. 

في الاقترانِ f(x) : $a =1 , b = 4$

بما أنَّ a > 0 ، فالتمثيل البيانيّ للقطع المُكافئ يكون مفتوحًا للأعلى، ويُمثل الرأس نقطتهُ الصغرى.  

• أَجِدُ مُعادلة محور التَّماثُل.

معادلة محور التماثل	$x = - \frac{b}{2a}$
بتعويض  $a =1 , b = 2$	$x = - \frac{4}{2\times 1}$
بالتبسيط	$x = -2$

 

 

 

 

 

إذن، مُعادلة محور التماثل هي  x = - 2

•  أَجِدُ إحداثِيَّيِ الرأسِ.

الاقتران المعطى	$f\left(x\right) = x^2+4x+1$
بتعويض x = -2	$f(-2) = {(-2)}^2+4(-2)+1$
بالتبسيط	$=-3$

إذن، إحداثيّا الرأسِ $(-2 , -3)$   

 

الخطوة 2 : أَجِدُ نقطةَ تقاطعِ الاقترانِ معَ المحورِ y.

لإيجادِ نقطةِ تقاطع الاقتران مع المحور y، أُعَوِّض x = 0 في قاعدة الاقتران.

الاقتران المعطى	$f\left(x\right) = x^2+4x+1$
بتعويض x = 0	$f\left(0\right) = 0^2+4\left(0\right)+1$
بالتبسيط	$=1$

 

 

 

 

إذنْ، نقطةُ تقاطعِ الاقترانِ معَ المحورِ y هِيَ (1 , 0).

الخطوة 3 : أَجِدُ نقطةً أُخرى باختيارِ قيمةٍ لِـ x تقعُ في الجانب الذي يقع فيه المقطع y يمين محور التماثل أو يسارَه.

أختار  x = - 1 

الاقتران المعطى	$f\left(x\right) = x^2+4x+1$
بتعويض x = - 1	$f(-1) = {(-1)}^2+4(-1)+1$
بالتبسيط	$= -2$

 

 

 

 

إذنْ، النقطةُ الأُخرى هِيَ (2- ,  1-).

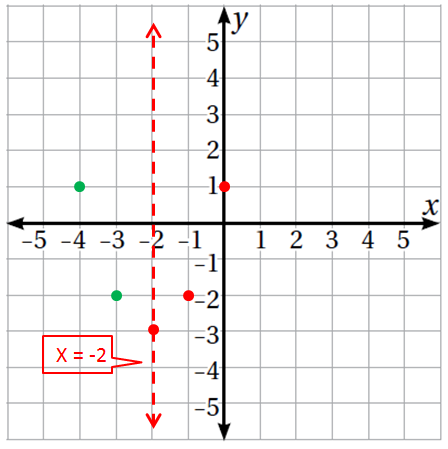
الخطوة 4 : أُمَثل النقاط في المُستوى الإحداثيِّ. أُمَثل رأس القطع والنقطتَيْن اللتَيْن أوجدتُهما من الخُطوتَيْن 2 وَ 3، وَهُما ( 1 , 0) وَ ( 2- , 1-)، ثمَّ أستعملُ التَّماثُلَ لأعكِسَ النقطتَيْنِ (1 , 0) وَ (2- , 1-) حول محور التماثُل؛ لإيجاد نقطتَيْن أُخرَيَيْن على التمثيل البيانيِّ.

 

 

 

 

 

 

 

 

 

•• أتعلَّم :  بما أنَّ محور التماثُل يقسِمُ القطع المُكافئ جُزأيْن متطابقَيْن فإنَّ لكلِّ نقطة على يسار هذا المحور نقطة تناظرُها على يمينِهِ وَتَبعُدُ عنهُ المسافةَ نفسَها، ويكونُ للنقطتَيْنِ الإحداثِيُّ y نفسُه.

 

 

 

الخطوة 5 : أصِلُ بين النقاط بمُنحنًى أملس.