الاقتران العكسي
نتذكر سويا أن العلاقة تربط بين مجموعتين من العناصر إحدهما تسمى المجال والأخرى تسمى المدى.
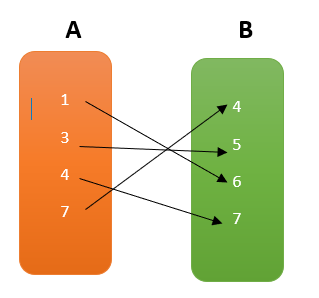
بالنظر للعلاقة الممثلة جانبا نلاحظ أن المجال هو و المدى هو
عند عكس اتجاه الأسهم لترتبط عناصر B بعناصر A تنتج علاقة عكسية ،مجالها B ، مداها A .
مثال :
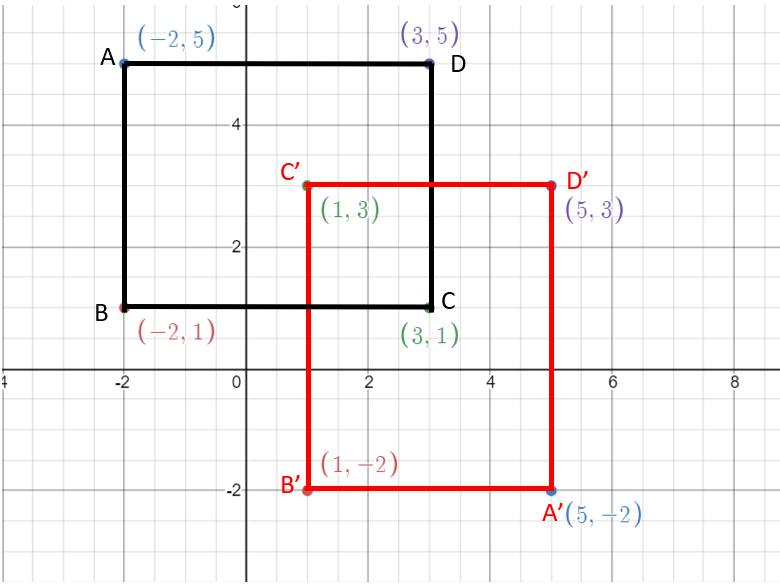
تمثل الأزواج المرتبة للعلاقة: إحداثيات رؤوس المستطيل ABCD. أجد العلاقة العكسية ، ثم أمثل بيانيا العلاقة والعلاقة العكسية على مستوى الإحداثي نفسه .
الحل :
لإيجاد العلاقة العكسية أبدل إحداثيي كل زوج مرتب، فتكون العلاقة العكسية هي :
عند تمثيل هذه الأزواج المرتبة بيانيا تنتج إحداثيات رؤوس المستطيل 'A' B' C' D الذي يمثل انعكاسا للمستطيل ABCD
- الاقترانات هي نوع خاص من العلاقات لأن لها خاصية لا تحققها جميع العلاقات فهي تربط كل عنصر في المجال بعنصر واحد فقط في المدى وبما أن كل اقتران هو علاقة فإنه يمكن إيجاد علاقة عكسية للأقتران ( معكوس الاقتران) فإذا كان المعكوس اقترانا أيضا يسمى اقترانا عكسيا ويرمز للاقتران العكسي للاقتران f(x) بالرمز
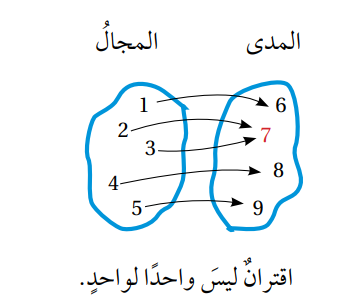
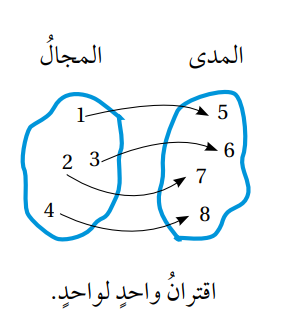
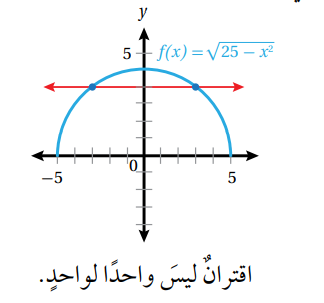
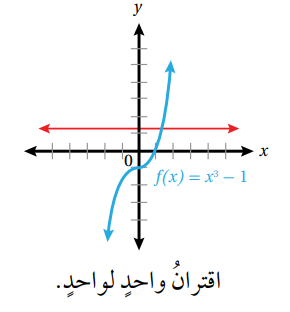
- يمكن تحديد إذا كان معكوس الاقتران f(x) يمثل اقترانا أم لا بالنظر إلى f(x) نفسه ، فإذا ارتبط كل عنصر في المدى بعنصر واحد فقط في المجال كان المعكوس اقترانا عندئذ يسمى f(x) اقتران واحد لواحد
- يمكن ايضا استعمال طريقة اختبار الخط الأفقي للتحقق من أن الاقتران هو اقتران واحد لواحد وذلك برسم أي خط أفقي والتأكد أنه لا يقطع منحنى الاقتران f(x) في أكثر من نقطة.
مفهوم أساسي
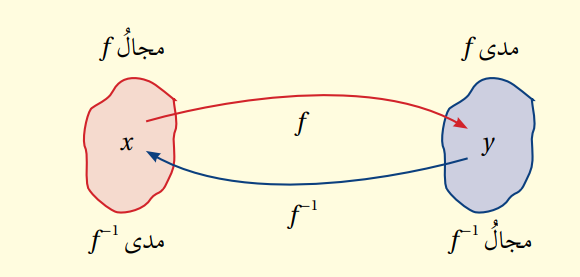
لأي اقتران f(x) يوجد اقتران عكسي f-1 (x) إذا كان f(x) اقتران واحد لواحد ، عندئذ يكون مجال f(x) هو مدى f-1 (x) و ، ومدى f(x) هو مجال f-1 (x) .
يمكن إيجاد الاقتران العكسي للاقتران المكتوب بصورة معادلة بالتبديل x و y في قاعدة الاقتران
مثال
أجد الاقتران العكسي في كل مما يلي :
1. f(x) = 4 (x-5)
الحل

عند تمثيل كل من f(x) و f-1 (x) في المستوى الإحداثي نفسه نلاحظ أن التمثيل البياني للاقتران f-1(x) هو انعكاس التمثيل البياني للاقتران f(x) حول المستقيم y= x
الحل
باستعمال إختبار الخط الأفقي نجد أن f(x) هو اقتران واحد لواحد عندما ، لذا له اقتران عكسي .
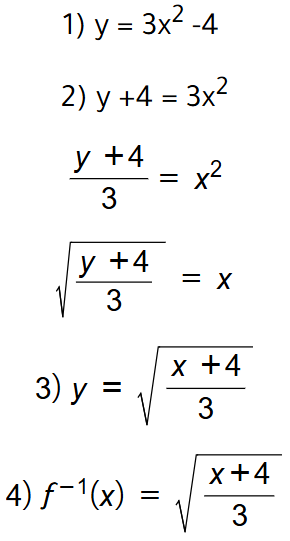
من خصائص أي اقترانين متعاكسين أن كلا منهما يعكس أثر الآخر ، لذا ينتج من تركيبهما الاقتران الذي يبقي كل عنصر في مجالهما على حاله و هو الاقتران المحايد الذي يربط كل عنصر بنفسه ، وقاعدته هي f(x) = x
نتيجة
يكون الاقتران العكسي للاقتران f(x) إذا وفقط إذا كان :
لجميع قيم x في مجال f -1(x) و لجميع قيم x في مجال f(X)
- تستعمل هذه النتيجة لإثبات أن كلا من اقترانين معلومين هو اقتران عكسي للآخر و للتحقق من صحة الحل عند إيجاد الاقتران العكسي
مثال
أثبت أن كل من الاقترانين و هو اقتران عكسي للآخر بإيجاد و
الحل:
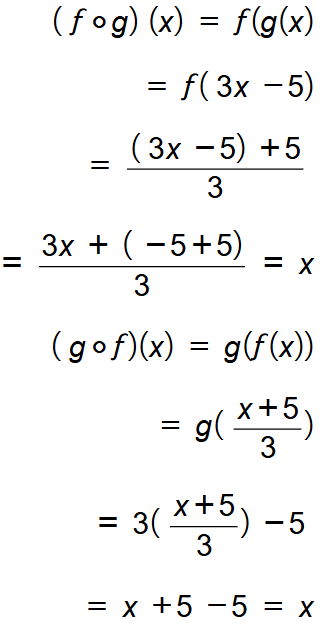
إذا كل من اقترانين f(X) و g(x) هو اقتران عكسي للآخر
لأن
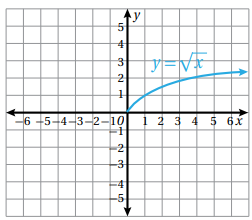
نتج من المثال السابق الاقتران العكسي الذي يحوي جذرا تربيعيا لمقدار جبري , وهو نوع خاص من الاقترانات يسمى الاقتران الجذري مثل :
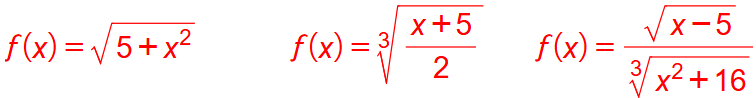

مثال
أجد مجال الأقتران ومداه ثم أجد الاقتران العكسي له .
الحل:
إذا مجال f(x) هو أو الفترة
ومداه جميع الأعداد الحقيقية من قيمته عند 3- فصاعدا أي أو الفترة
لإيجاد الأقتران العكسي
يكون مجال f-1 (x) هو مدى f(x)
أي مجاله
ومداه هو مجال f(x)
أي مداه
يستخدم مفهوم الاقتران العكسي في حل بعض المسائل الحياتية
مثال
سقط جسيم ساكن من ارتفاع 200m عن سطح الأرض فكان ارتفاعه h عن الأرض بالأمتار بعد t ثانية من سقوطه هو
أعبر عن t بصورة اقتران بدلالة الإرتفاع h ثم أجد الزمن الذي يكون فيه ارتفاع الجسيم 50m فقط
الحل
إذا الاقتران الذي يعبر عن الزمن بدلالة الإرتفاع هو
إذا يكون الجسيم على إرتفاع 50m بعد مضي 5.53 ثانية تقريبا من لحظة سقوطه